//二叉树的表示
typedef struct TNode* BinTree; struct TNode { ElementType Data; BinTree Left; BinTree Right; }; //二叉树 前序 非递归 void InOrderTraversal(BinTree BT) { BinTree T = BT; Stack S = CreateStack(MaxSize); while(T || !IsEmpty(S)) { while(T) //直到左子树为空停止向左下访问 { Push(S,T); printf("T->Data"); //由于为前序遍历,当第一次遇到根节点就打印他 T = T->Left; } if(!IsEmpty(S)) { T = Pop(S); T = T->Right; //开始访问右子树 } } } //二叉树 中序遍历 非递归 void MidOrderTraversal(BinTree BT) { BinTree T = BT; Stack S = CreateStack(MaxSize); while(T || !IsEmpty(S)) { while(T) { Push(S,T); T = T->Left; } if(!IsEmpty(S)) { T = Pop(S); printf("T->Data"); //当第二次遇到根节点则打印他 T = T->Right; } } } //二叉树的表示 typedef struct TNode* BinTree; typedef struct TNode* BinTree; struct TNode { ElementType Data; BinTree Left; BinTree Right; int flag; //用一个flag记录是第几次遇到根节点 }; //二叉树 后序遍历 非递归 void UnOrderTraversal(BinTree BT) { BinTree T = BT; Stack S = CreateStack(MaxSize); while(T || !IsEmpty(S)) { while(T) { Push(S,T); T->flag = 1; T = T->Left; }
if(!isEmpty(S))
{ T = Top(S); if(T->flag == 1) //当第二次遇到根节点,则不应当将其弹出,而是访问其右子树 { T->flag++; T = T->Right; }else if(T->flag == 2) //第三次遇到根节点,此时左右子树都访问完了,可以打印并弹出他了 { printf(T->Data); Pop(S);
T = NULL; }
} } }
一张图表示非递归遍历的实质:
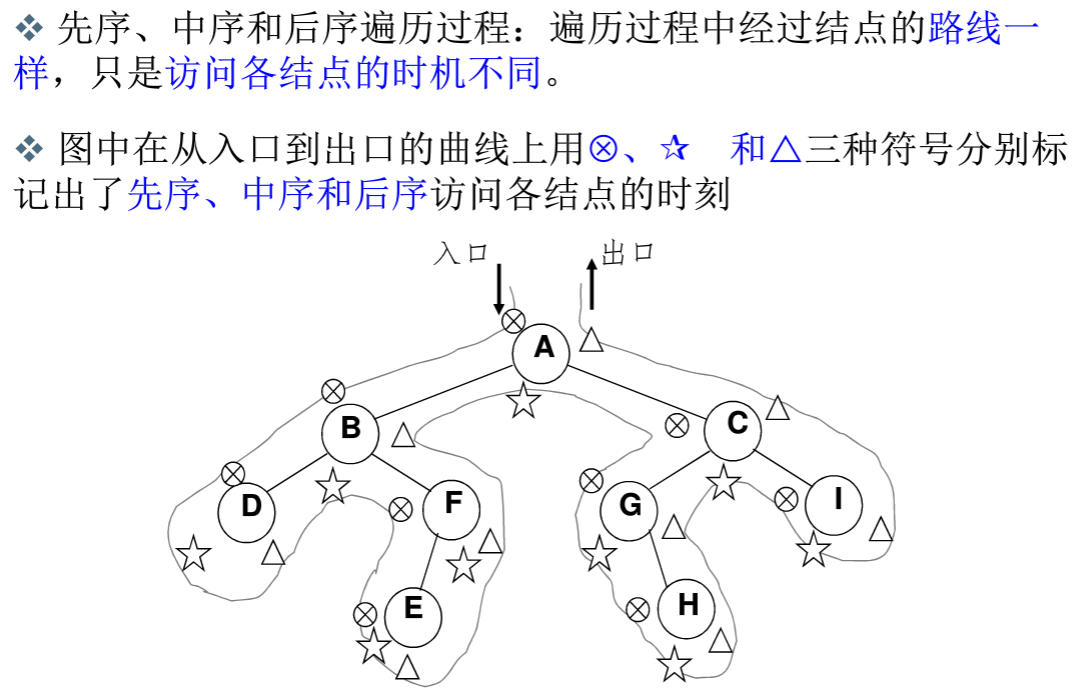
我们如何找到左子树,因为我们先访问根节点,所以根据根节点中保存的左子树的地址,可以向左下访问。
那左子树访问完了,如何回来访问右子树呢?
这就是栈的作用!!!!
栈顶保存着上一次最后遇到的根节点,把栈顶元素弹出,则可以“往回走”,借此可以访问右子树。