Tower Defense Game

Tower Defense Game

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

There is a tower defense game with n levels(missions). The n levels form a tree whose root is level 1.

In the i-th level, you have to spend pi units of money buying towers and after the level, you can sell the towers so that you have qi units of money back.

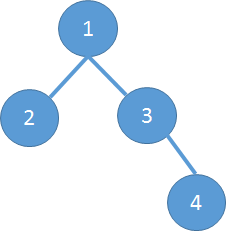
Each level is played once. You can choose any order to complete all the levels, but the order should follow the following rules:

1: A level can be played when all its ancestors are completed.

2: The levels which form a subtree of the original tree should be completed consecutively in your order.

You want to know in which order of completion you can bring the minimum money before starting the first level.

输入

The first line contains one single integers, n - the number of levels. (1<=n<=10000)

The next n lines describes the levels. Each line contains 2 integers, pi and qi which are described in the statement. (0<=qi<=pi<=20000)

The next n-1 lines describes the tree. Each line contains 2 integers, ai and bi which means there is an edge between level ai and level bi.

For 30% of the data, n<=100.

For 60% of the data, n<=1000.

输出

Print one line with an single integer representing the minimum cost.

样例提示

There are two orders of completing all levels which are: 1234 and 1342.

In the order 1234, the minimum beginning money is 5.

In the order 1342, the minimum beginning money is 7.

1324 is not a valid order because level 3 and level 4 are not completed consecutively.

样例输入

4
2 1
4 3
2 1
2 1
1 2
1 3
3 4

样例输出

　　　5

分析：题目大意是给你一棵树，每个节点都有支出和收入，问你从1号根节点深搜完所有节点至少要带多少钱？

　　　假设你带的钱很多，那该怎么走呢？

　　　你到了某一结点，应该走其中一棵子树，使得你走完之后剩下的钱最多，这样必定是最优的；

　　　所以dfs回溯求解，最后回溯到1号节点就是答案；

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#include <ext/rope>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define vi vector<int>
#define pii pair<int,int>
#define mod 1000000007
#define inf 0x3f3f3f3f
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
const int maxn=1e4+10;
const int dis[4][2]={{0,1},{-1,0},{0,-1},{1,0}};
using namespace std;
using namespace __gnu_cxx;
ll gcd(ll p,ll q){return q==0?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=1;while(q){if(q&1)f=f*p;p=p*p;q>>=1;}return f;}
int n,m,p[maxn],q[maxn],vis[maxn];
vi a[maxn];
pii ans[maxn];
bool cmp(const int&x,const int&y)
{
    return ans[x].se>ans[y].se;
}
pii dfs(int s)
{
    vis[s]=1;
    vi son;
    ans[s]={p[s],q[s]};
    for(int x:a[s])if(!vis[x])ans[x]=dfs(x),son.pb(x);
    sort(son.begin(),son.end(),cmp);
    for(int x:son)
    {
        if(ans[x].fi>ans[s].se)ans[s].fi+=ans[x].fi-ans[s].se,ans[s].se=ans[x].se;
        else ans[s].se+=ans[x].se-ans[x].fi;
    }
    return ans[s];
}
int main()
{
    int i,j,k,t;
    scanf("%d",&n);
    rep(i,1,n)scanf("%d%d",&p[i],&q[i]);
    rep(i,1,n-1)scanf("%d%d",&j,&k),a[j].pb(k),a[k].pb(j);
    dfs(1);
    printf("%d
",ans[1].fi);
    //system ("pause");
    return 0;
}