编码运算中的溢出判断，无符号数，有符号数，原码，补码

在计算机系统中编码以二进制形式存在，而且受到机器字长的限制，在编码运算过程中可能会出现运算结果超出机器数表示范围的情况，称为“溢出”。溢出的计算结果是不可靠的。“溢出”指运算结果超出机器数表示范围。

一．无符号数编码运算中的溢出判断：

　　加法运算，如果运算结果超位了，则为溢出；减法运算，如果是小的减大的，则必溢出。

二．带符号数编码运算中的溢出判断：

　　原码和补码的减法运算都是先将a-b转换为a+(-b)，然后加法运算。因此下面我们只说加法运算。

1. 原码的运算：正正相加或者负负相加只看有没有超位，超了则溢出。正负相加不会溢出。
2. 补码的运算：这是本文核心，因为计算机系统中采用的都是补码的编码形式，说的通俗点，存在计算机系统上的数都是补码形式。对于补码加法运算结果的溢出判断，正正相加或者负负相加，如果运算结果的符号位发生变化则发生溢出。

　　8位补码运算的例子：

　　01111010 + 00101000 = 10100010，发生溢出，结果不可靠。

　　11111010 + 10100001 = 10011011，发生溢出，结果不可靠。

　　——————————————————————————————

　　补充一下，原码补码(图片来自网络，侵删)

　　

　　——————————————————————————————

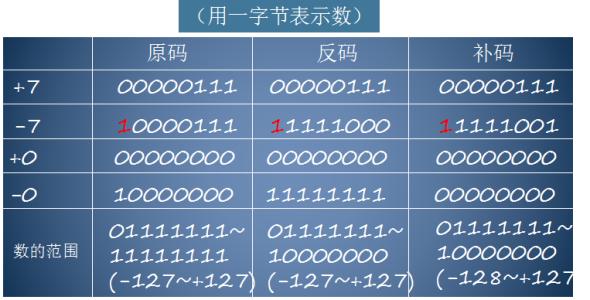
三. 浮点运算中的溢出判断：

　　以32位浮点为例，在计算机中浮点数是这样存在的————一个32位浮点数总共占用4个字节的空间(8位为一个字节)，也就是32个比特。第31位为符号位(s)，第30~23位为指数域(E)，第22~0位为尾数域(F)。一般浮点数表示为这样的形式： (-1)^s x F x 2^E  。(补充：在64位浮点中指数域占11位，尾数域占52位)