一、为什么对数据归一化
我们知道在神经网络训练开始前,需要对输入数据做归一化处理,那么具体为什么需要归一化呢?
原因在于:神经网络学习过程本质就是为了学习数据特征以及数据的分布特征,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
同时也是在训练前为什么要把训练数据充分打乱的原因,充分打乱使得每个batch的样本包含各类别的数据,这样通过每个batch的样本训练时各个batch所包含的数据分布更接近,同时和整个训练集的数据分布更接近,更有利于训练出更泛化的模型,同时有利于模型的收敛。试想不充分打乱数据,若每个batch只包含一个类别的数据,不同的batch数据进行训练时网络就要在每次迭代都去学习适应不同的分布,会使得网络收敛很慢。
二、数据进行归一化标准化常用的方法
数据的标准化(正则化)以及归一化之间的界限很模糊,现在都进行混用,常用的方法有,最小最大值归一化以及z-score标准化

标准差是方差的算术平方根
来源于:https://blog.csdn.net/xiaotao_1/article/details/79077293
三、Batch Normalization
1.算法的诞生
上文提到神经网络的本质是学习数据结构的特征以及数据的分布特征。对于深度网络的训练是一个复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。
网络的训练是对可训练参数不断更新的过程,除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的,因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。数据分布的改变称之为:“Internal Covariate Shift”。为了解决在训练过程中,中间层数据分布发生改变的情况,于是就有了Batch Normalization。
2.Batch Normalization概述
如其名Batch Normalization是以一个batch为基本单位,对每个神经元做归一化处理,同时Batch Normalization(BN)和隐藏层、卷积层等一样是网络结构中的一层,一般应用在激活函数前。在没有采用BN的时候,激活函数层是这样的:
z=g(Wu+b)
也就是我们希望一个激活函数,比如s型函数s(x)的自变量x是经过BN处理后的结果。因此前向传导的计算公式就应该是:
z=g(BN(Wu+b))
其实因为偏置参数b经过BN层后其实是没有用的,最后也会被均值归一化,当然BN层后面还有个β参数作为偏置项,所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了:
z=g(BN(Wu))
3.Batch Normalization的计算
注意Batch Normalization的计算不是只简单的通过归一化公式事先对网络某一层A的输出数据做归一化,然后送入网络下一层B,这样是会影响到本层网络A所学习到的特征的。打个比方,比如我网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧,你强制把它给我归一化处理、标准差也限制在了1,把数据变换成分布于s函数的中间部分,这样就相当于我这一层网络所学习到的特征分布被搞坏了,原文中提出了一种变换重构的方法,引入了可学习参数γ、β,这就是算法关键之处,让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式如下,其中的ε是一个很小的数,用于防止除0。


4.Batch Normalization在测试数据上的使用
上面的算法是在训练过程中的应用,测试阶段假设我们想只输入一个测试样本,看看结果而已。因此测试样本,前向传导的时候,上面的均值u、标准差σ 要哪里来?其实网络一旦训练完毕,参数都是固定的,这个时候即使是每批训练样本进入网络,那么BN层计算的均值u、和标准差都是固定不变的。我们可以采用这些数值来作为测试样本所需要的均值、标准差。
对于测试集均值和方差已经不是针对某一个Batch了,而是针对整个数据集而言。因此,在训练过程中除了正常的前向传播和反向求导之外,我们还要记录每一个Batch的均值和方差,以便训练完成之后按照下式计算整体的均值和方差:

上面简单理解就是:对于均值来说直接计算所有batch u值的平均值;然后对于标准偏差采用每个batch σB的无偏估计。最后测试阶段,BN的使用公式就是:

5.Batch Normalization的作用
1)改善流经网络的梯度
2)允许更大的学习率,大幅提高训练速度:
你可以选择比较大的初始学习率,让你的训练速度飙涨。以前还需要慢慢调整学习率,甚至在网络训练到一半的时候,还需要想着学习率进一步调小的比例选择多少比较合适,现在我们可以采用初始很大的学习率,然后学习率的衰减速度也很大,因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率,也比以前的收敛速度快,因为它具有快速训练收敛的特性;
3)减少对初始化的强烈依赖
4)改善正则化策略:作为正则化的一种形式,轻微减少了对dropout的需求
你再也不用去理会过拟合中drop out、L2正则项参数的选择问题,采用BN算法后,你可以移除这两项了参数,或者可以选择更小的L2正则约束参数了,因为BN具有提高网络泛化能力的特性;
5)再也不需要使用使用局部响应归一化层了(局部响应归一化是Alexnet网络用到的方法,搞视觉的估计比较熟悉),因为BN本身就是一个归一化网络层;
6)可以把训练数据彻底打乱(防止每批训练的时候,某一个样本都经常被挑选到,文献说这个可以提高1%的精度)。
6.Batch Normalization的缺点
1)受batch_size大小的限制
BN是以batch为单位计算归一化统计量的,当一个batch样本数很少时,少量样本的均值和方差无法反映全局的统计分布,所以基于少量样本的BN的效果会变得很差。在一些场景中,比如说硬件资源受限,在线学习等场景,BN是非常不适用的。(在Transformer中使用的是Layer Normalization,受硬件的限制,Bert一般训练的批次都不大)
2)无法很好的应用于RNN中
在一个batch中,通常各个样本的长度都是不同的,当统计到比较靠后的时间片时,这时可能只有很少的样本数据为非零值,基于这些仍有数据的少量样本的统计信息不能反映全局分布,所以这时BN的效果并不好。
另外如果在测试时我们遇到了长度大于任何一个训练样本的测试样本,我们无法找到保存的归一化统计量,所以BN无法运行。
四、Layer Normalization
LN是一个独立于batch size的算法,所以无论一个batch样本数多少都不会影响参与LN计算的数据量,从而解决BN的两个问题。LN的做法是根据样本的特征数做归一化。
设 H是一层中隐层节点的数量,l 是隐藏的层数,我们可以计算LN的归一化统计量 (均值)和
(标准差):

五、Batch Normalization和Layer Normalization的对比分析
Batch Normalization 是对这批样本的同一维度特征(每个神经元)做归一化, Layer Normalization 是对这单个样本的所有维度特征做归一化。
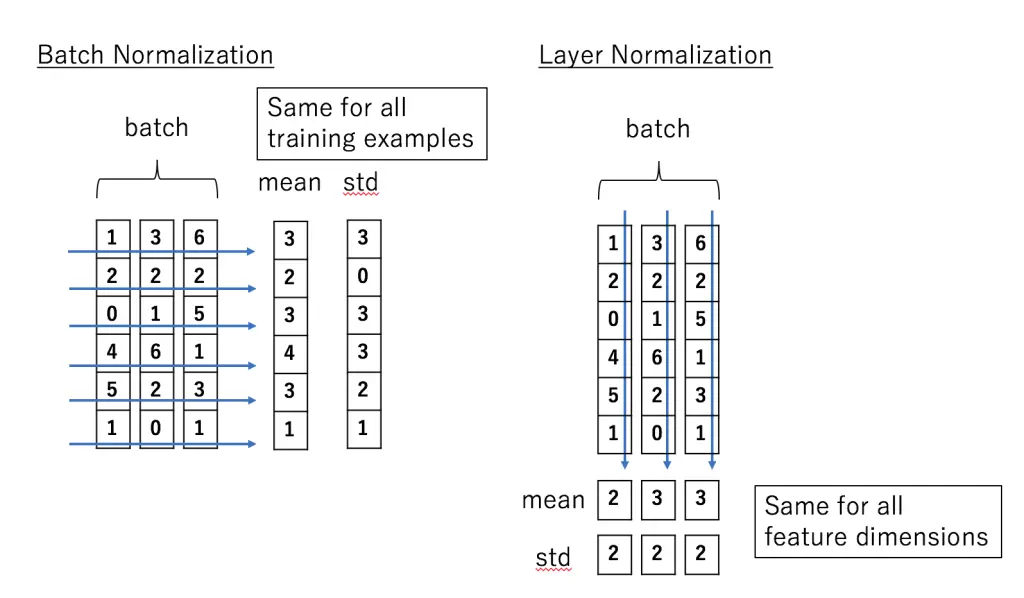
实践证明,LN用于RNN进行Normalization时,取得了比BN更好的效果。但用于CNN时,效果并不如BN明显。
以上内容是对如下的总结
https://blog.csdn.net/qq_41853758/article/details/82930944
https://zhuanlan.zhihu.com/p/54530247
https://www.jianshu.com/p/367c456cc4cf
Layer Normalization论文地址:https://arxiv.org/pdf/1607.06450.pdf
Batch Normalization论文地址:https://arxiv.org/pdf/1502.03167.pdf