数据结构--二叉查找树

定义

二叉查找树：即BST，也叫二叉搜索树，二叉排序树，在二叉树的基础上，它拥有如下性质，每个节点的值都大于其左子树中的任意节点的值，而小于右子树的任意节点

图例

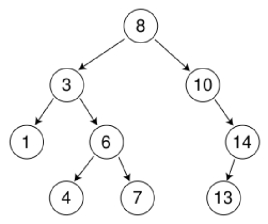
 数据结构

　　节点数据结构如下

private class Node {
        private Value value; //该节点的值
        private Node left,right;//该节点的左右子树
        
        public Node(Value value) {
            this.value = value;
        }
    }

查找过程

　　递归可以使查找过程清晰易懂

//在树中查找节点
    public Node get(Value value) {
        return get(root, value); // 从根节点开始查找
    }
    private Node get(Node x, Value value) {
        if (x == null) {
            return null;
        }
        int cmp = value.compareTo(x.value);
        if (cmp < 0) //如果目标值小于当前节点的值，则递归查找当前节点的左子树
            return get(x.left, value);
        else if (cmp > 0)//如果目标值大于当前节点值，则递归查找当前节点的右子树
            return get(x.right, value);
        else //相等则返回当前节点的引用
            return x;
    }

　　比如要在上图查找结点值为4的节点，从根节点开始→4小于8，则查找左子树→4大于3，则查找右子树→4小于6，则查找左子树→查找成功

插入过程

　　插入过程和查找过程极其相似，只是在最后多了一步添加结点的操作

//插入节点
    public void put(Value value) {
        //查找节点位置
        root = put(root,value);
    }
    private Node put(Node x, Value value) {
        if (x == null) {
            return new Node(value);
        }
        int cmp = value.compareTo(x.value);
        if (cmp < 0) {
            x.left = put(x.left,value);
        }else if (cmp > 0)  {
            x.right = put(x.right,value);
        }
        return x;
    }

　　二叉查找树的优势：这里借用算法4书上的一张表

　　

 　　对比二分查找，在查找性能下降些许的情况下，却可以将插入复杂度下降一个等级的复杂度，是非常不错的。

 

注意：

　　1.同一集合，由于插入的顺序不同，可能有多种不同的树结构

　　

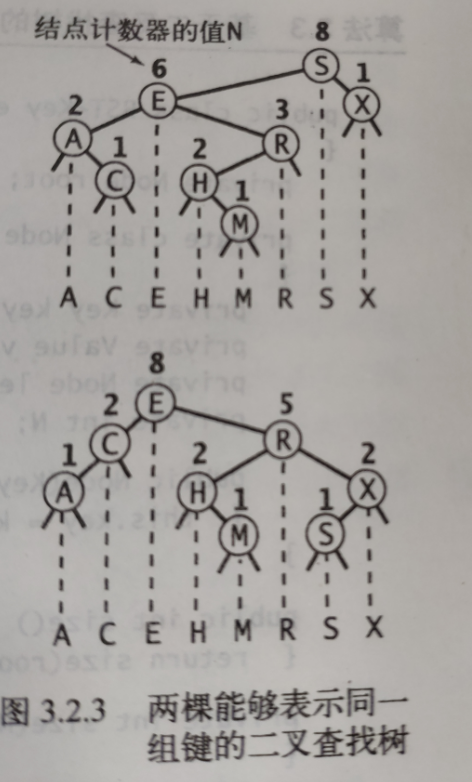
 　　2.在最好的情况下，二叉查找树的N个节点是平衡的（即叶子节点的深度差不超过1），最差时，二叉查找树退化为链表

　　

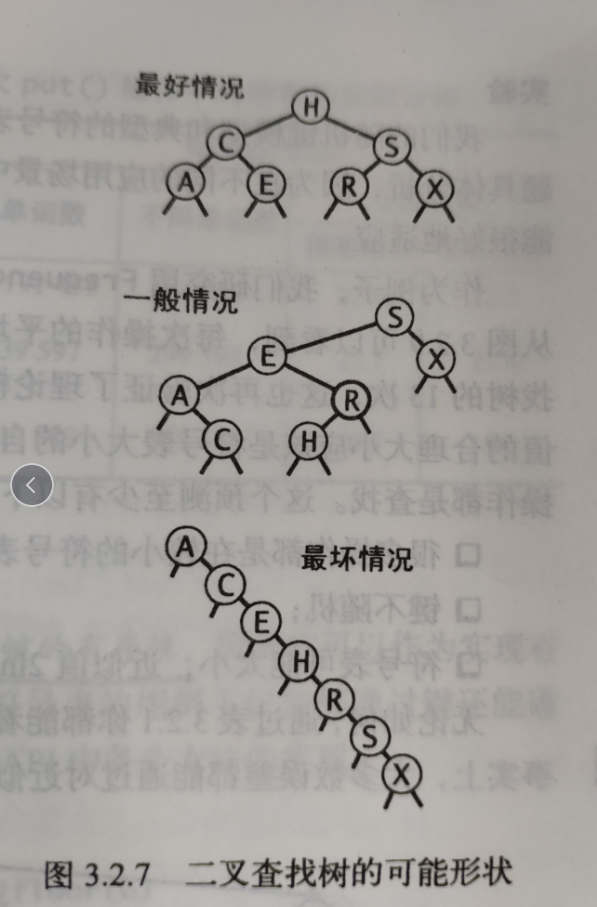
延伸：

　这里的实现只是简单实现了树的构造和查找，有以下可以深入了解的点：

　　1.将节点元素值换为键值对，以方便存储符号表

　　2.二叉查找树的最大、最小、删除、范围查找等

 

最后给出一个完整代码

　　

public class BST<Value extends Comparable<Value>> {
    private Node root;
    private class Node {
        private Value value; //该节点的值
        private Node left,right;//该节点的左右子树

        public Node(Value value) {
            this.value = value;
        }
    }

    //在树中查找节点
    public Node get(Value value) {
        return get(root, value); // 从根节点开始查找
    }
    private Node get(Node x, Value value) {
        if (x == null) {
            return null;
        }
        int cmp = value.compareTo(x.value);
        if (cmp < 0) //如果目标值小于当前节点的值，则递归查找当前节点的左子树
            return get(x.left, value);
        else if (cmp > 0)//如果目标值大于当前节点值，则递归查找当前节点的右子树
            return get(x.right, value);
        else //相等则返回当前节点的引用
            return x;
    }

    //插入节点
    public void put(Value value) {
        //查找节点位置
        root = put(root,value);
    }
    private Node put(Node x, Value value) {
        if (x == null) {
            return new Node(value);
        }
        int cmp = value.compareTo(x.value);
        if (cmp < 0) {
            x.left = put(x.left,value);
        }else if (cmp > 0)  {
            x.right = put(x.right,value);
        }
        return x;
    }
}