HDU 6574 Rng (概率，乘法原理)

Rng

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 624    Accepted Submission(s): 411

Problem Description

Avin is studying how to synthesize data. Given an integer n, he constructs an interval using the following method: he first generates a integer r between 1 and n (both inclusive) uniform-randomly, and then generates another integer l between 1 and r (both inclusive) uniform-randomly. The interval [l, r] is then constructed. Avin has constructed two intervals using the method above. He asks you what the probability that two intervals intersect is. You should print p* q(−1)(MOD 1, 000, 000, 007), while pq denoting the probability.

 

Input

Just one line contains the number n (1 ≤ n ≤ 1, 000, 000).

 

Output

Print the answer.

 

Sample Input

1 2

 

Sample Output

1 750000006

 

Source

2019CCPC-江西省赛（重现赛）- 感谢南昌大学

 

Recommend

liuyiding

 

题意：给定一个 n ，你可以构造出两个区间，求这两个区间相交的概率是多少，构造的方式就是首先在 [1, n] 内随机选一个点 R，然后再在 [1, R] 随机选另一点 L，形成区间 [L, R]，两次构造过程是独立的。

析：假设两个区间的右端点是 a, b，然后可以得到对于给定的 a 和 b，不相交的概率为 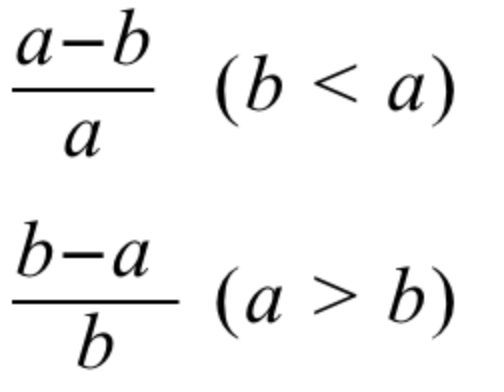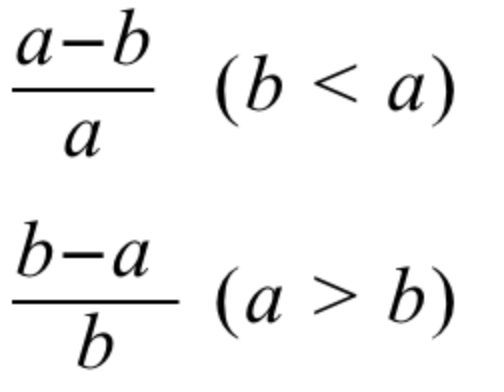，然后就可以枚举a和b，可以得到下式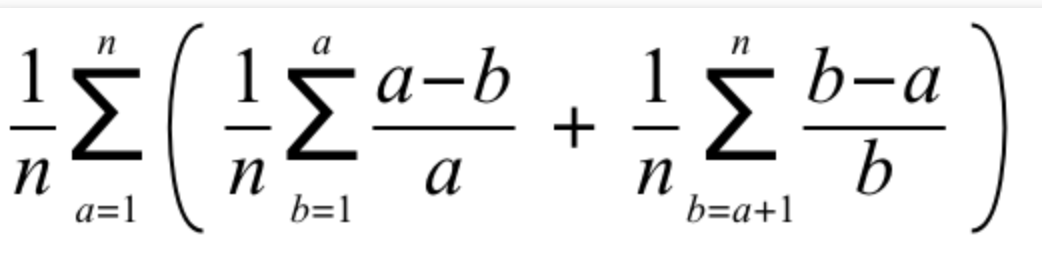

化简得到

 然后使用逆元就可以求了。

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
// #define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define be begin()
#define ed end()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
#define all 1,n,1
#define FOR(i,n,x)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.in", "r", stdin)
#define freopenw freopen("out.out", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 100 + 7;
const int maxm = 2000000 + 7;
const LL mod = 1e9 + 7;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
int n, m;

inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}
inline int readInt(){
  int x;  cin >> x;  return x;
}

const LL inv2 = 500000004L;

LL fast_pow(LL a, int n){
  LL res = 1;
  while(n){
    if(n&1)  res = res * a % mod;
    n >>= 1;
    a = a * a % mod;
  }
  return res;
}


int main(){
  while(cin >> n)  cout << (inv2 + fast_pow(n<<1, mod-2)) % mod << endl;
}