在之前的博文中,为大家介绍过ArcGIS中的地理坐标系和投影坐标系(或称大地坐标系)(http://blog.csdn.net/arcgis_all/article/details/8216583),这里面简要的说明了两者的概念及关系。接下来,针对这块的GIS理论基础,将做个系统全面的介绍,希望为各位带来帮助。
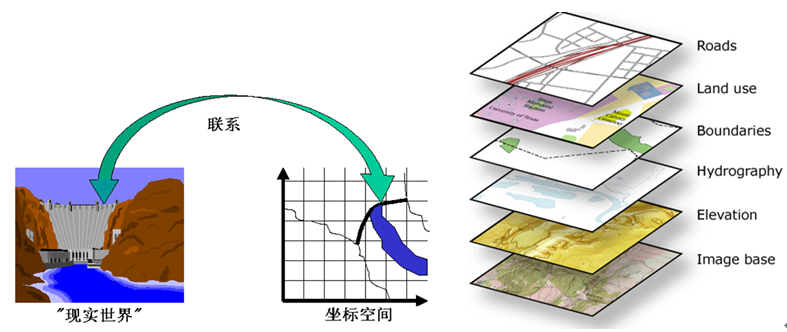
1、现实世界和坐标空间的联系
任何空间特征都表示为地球表面的一个特定位置,而位置依赖于既定的坐标系来表示。 通过统一的坐标系和高程系,可以使不同源的GIS数据叠加在一起显示,以及执行空间分析。
2、地球空间模型描述
为了深入研究地理空间,需要建立地球表面的几何模型,这是进行大地测量的前提。根据大地测量学的成果,地球表面几何模型可以分为三类:
1) 第一类是地球的自然表面。

2) 第二类是相对抽象的面,即大地水准面,可用来代表地球的物理化形状。其中大地水准面包围的球体,叫大地球体,是对地球形体的一级逼近。
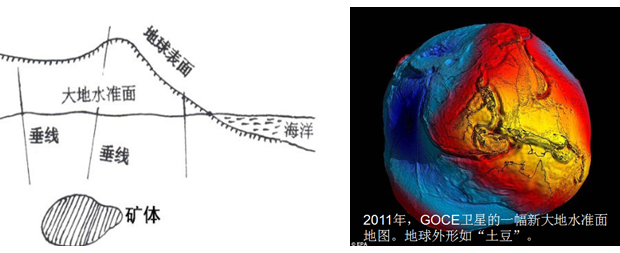
地球上有71%的海洋面积,因此可以假设当海水处于完全静止的平衡状态时,从海平面延伸到所有大陆下部,而与地球重力方向处处正交的一个连续、闭合的曲面,这就是大地水准面。它是重力等位面。
3) 第三类是以大地水准面为基准建立起来的地球椭球体模型。
大地水准面虽然十分复杂,但从整体来看,起伏是微小的,且形状接近一个扁率极小的椭圆绕短轴旋转所形成的规则椭球体,这个椭球体称为地球椭球体。其表面是一个规则数学表面,可用数学公式表达,所以在测量和制图中用它替代地球的自然表面。地球形体的二级逼近。
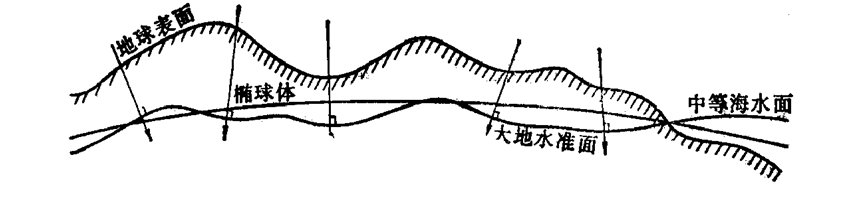
地球椭球体有长半径a(赤道半径)和短半径b(极半径)之分,f为椭圆的扁率。a、b、f是其三要素,决定地球椭球体的形状和大小。

各种地球椭球体模型(参考椭球体,下面会介绍)如下图所示。
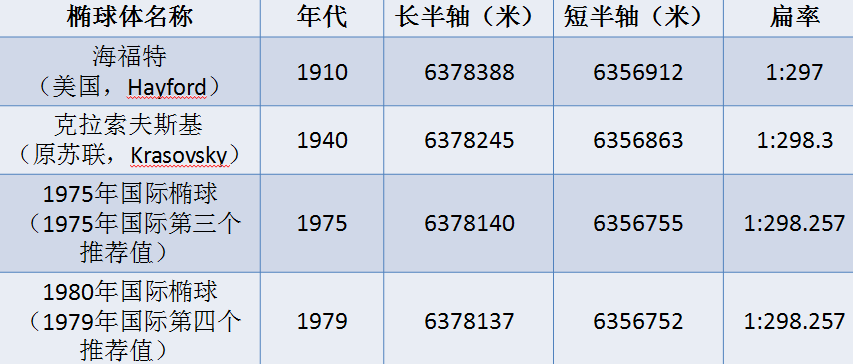
我国1952年以前采用海福特椭球体,从1953年起采用克拉索夫斯基椭球体。 1978年我国决定采用新椭球体GRS(1975),并以此建立了我国新的、独立的大地坐标系,对应ArcGIS里面的Xian_1980椭球体。从1980年开始采用新椭球体GRS(1980),这个椭球体参数与ArcGIS中的CGCS2000椭球体相同。
地球椭球体视为球体:制作小比例尺地图时(小于1:500万),因缩小程度很大,可以把地球视为球体,忽略地球扁率。计算更简单,半径约为6371千米。
地球椭球体视为椭球体:制作大比例尺地图时(大于1:100万),为保证精度,必须将地球视为椭球体。
——下篇介绍“地理坐标系”
原文链接:http://blog.csdn.net/arcgis_all/article/details/8834848