Java中排序可以分为内部排序,外部排序具体如下:

这里我们讨论选择排序、冒泡排序、快速排序
选择排序
在要排序的一组数中,选出最小(或者最大)的一个数与第1个位置的数交换;然后在剩下的数当中再找最小(或者最大)的与第2个位置的数交换,依次类推,直到第n-1个元素(倒数第二个数)和第n个元素(最后一个数)比较为止。
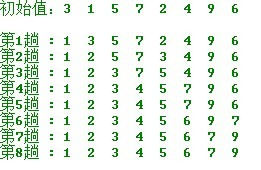
操作方法:
第一趟,从n 个记录中找出关键码最小的记录与第一个记录交换;
第二趟,从第二个记录开始的n-1 个记录中再选出关键码最小的记录与第二个记录交换;
以此类推.....
第i 趟,则从第i 个记录开始的n-i+1 个记录中选出关键码最小的记录与第i 个记录交换,
直到整个序列按关键码有序。
package com;
public class SimpleSelectSort {
public static void main(String[] args) {
int a[] = {3,1,5,7,2,4,9,6,10,8};
SimpleSelectSort obj=new SimpleSelectSort();
System.out.println("初始值:");
obj.print(a);
obj.selectSort(a);
System.out.println("
排序后:");
obj.print(a);
}
private void selectSort(int[] a) {
for(int i=0;i<a.length;i++){
int k=i;//k存放最小值下标。每次循环最小值下标+1
for(int j=i+1;j<a.length;j++){//找到最小值下标
if(a[k]>a[j])
k=j;
}
swap(a,k,i);//把最小值放到它该放的位置上
}
}
public void print(int a[]){
for(int i=0;i<a.length;i++){
System.out.print(a[i]+" ");
}
}
public void swap(int[] data, int i, int j) {
if (i == j) {
return;
}
data[i] = data[i] + data[j];
data[j] = data[i] - data[j];
data[i] = data[i] - data[j];
}
}
简单选择排序改进
简单选择排序,每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素(当前趟最大和最小记录)的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序,最多只需进行[n/2]趟循环即可。具体实现如下:
冒泡排序
基本思想:
在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
冒泡排序的示例:
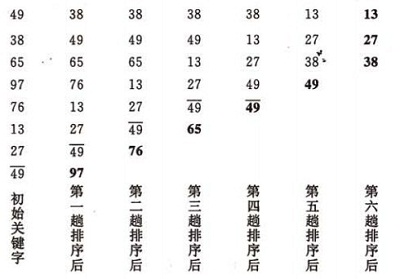
void bubbleSort(int a[], int n){
for(int i =0 ; i< n-1; ++i) {
for(int j = 0; j < n-i-1; ++j) {
if(a[j] > a[j+1])
{
int tmp = a[j] ; a[j] = a[j+1] ; a[j+1] = tmp;
}
}
}
}
冒泡排序算法的改进
对冒泡排序常见的改进方法是加入一标志性变量exchange,用于标志某一趟排序过程中是否有数据交换,如果进行某一趟排序时并没有进行数据交换,则说明数据已经按要求排列好,可立即结束排序,避免不必要的比较过程。本文再提供以下两种改进算法:
1.设置一标志性变量pos,用于记录每趟排序中最后一次进行交换的位置。由于pos位置之后的记录均已交换到位,故在进行下一趟排序时只要扫描到pos位置即可。
改进后算法如下:
void Bubble_1 ( int r[], int n) {
int i= n -1; //初始时,最后位置保持不变
while ( i> 0) {
int pos= 0; //每趟开始时,无记录交换
for (int j= 0; j< i; j++)
if (r[j]> r[j+1]) {
pos= j; //记录交换的位置
int tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp;
}
i= pos; //为下一趟排序作准备
}
}
2.传统冒泡排序中每一趟排序操作只能找到一个最大值或最小值,我们考虑利用在每趟排序中进行正向和反向两遍冒泡的方法一次可以得到两个最终值(最大者和最小者) , 从而使排序趟数几乎减少了一半。
改进后的算法实现为:
void Bubble_2 ( int r[], int n){
int low = 0;
int high= n -1; //设置变量的初始值
int tmp,j;
while (low < high) {
for (j= low; j< high; ++j) //正向冒泡,找到最大者
if (r[j]> r[j+1]) {
tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp;
}
--high; //修改high值, 前移一位
for ( j=high; j>low; --j) //反向冒泡,找到最小者
if (r[j]<r[j-1]) {
tmp = r[j]; r[j]=r[j-1];r[j-1]=tmp;
}
++low; //修改low值,后移一位
}
}
快速排序
基本思想:
1)选择一个基准元素,通常选择第一个元素或者最后一个元素,
2)通过一趟排序讲待排序的记录分割成独立的两部分,其中一部分记录的元素值均比基准元素值小。另一部分记录的 元素值比基准值大。
3)此时基准元素在其排好序后的正确位置
4)然后分别对这两部分记录用同样的方法继续进行排序,直到整个序列有序。
快速排序的示例:
(a)一趟排序的过程:

(b)排序的全过程

算法的实现:
递归实现:
package com;
public class QuickSort {
public static void main(String[] args) {
int a[] = {3,1,5,7,2,4,9,6,10,8};
QuickSort obj=new QuickSort();
System.out.println("初始值:");
obj.print(a);
int h=a.length-1;
obj.quickSort(a,0,h);
System.out.println("
排序后:");
obj.print(a);
}
private void quickSort(int[] a,int low, int high) {
if(low<high){ //如果不加这个判断递归会无法退出导致堆栈溢出异常
int middle=getMiddle(a,low,high);
quickSort(a, 0, middle-1); //递归对低子表递归排序
quickSort(a, middle + 1, high); //递归对高子表递归排序
}
}
public int getMiddle(int[] a, int low, int high){
int key = a[low];//基准元素,排序中会空出来一个位置
while(low<high){
while(low<high && a[high]>=key){//从high开始找比基准小的,与low换位置
high--;
}
a[low]=a[high];
while(low<high && a[low]<=key){//从low开始找比基准大,放到之前high空出来的位置上
low++;
}
a[high]=a[low];
}
a[low]=key;//此时low=high 是基准元素的位置,也是空出来的那个位置
return low;
}
public void print(int a[]){
for(int i=0;i<a.length;i++){
System.out.print(a[i]+" ");
}
}
}
分析:
快速排序是通常被认为在同数量级(O(nlog2n))的排序方法中平均性能最好的。但若初始序列按关键码有序或基本有序时,快排序反而蜕化为冒泡排序。为改进之,通常以“三者取中法”来选取基准记录,即将排序区间的两个端点与中点三个记录关键码居中的调整为支点记录。快速排序是一个不稳定的排序方法。
快速排序的改进
在本改进算法中,只对长度大于k的子序列递归调用快速排序,让原序列基本有序,然后再对整个基本有序序列用插入排序算法排序。实践证明,改进后的算法时间复杂度有所降低,且当k取值为 8 左右时,改进算法的性能最佳。算法思想如下:
void print(int a[], int n){
for(int j= 0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
int partition(int a[], int low, int high)
{
int privotKey = a[low]; //基准元素
while(low < high){ //从表的两端交替地向中间扫描
while(low < high && a[high] >= privotKey) --high; //从high 所指位置向前搜索,至多到low+1 位置。将比基准元素小的交换到低端
swap(&a[low], &a[high]);
while(low < high && a[low] <= privotKey ) ++low;
swap(&a[low], &a[high]);
}
print(a,10);
return low;
}
void qsort_improve(int r[ ],int low,int high, int k){
if( high -low > k ) { //长度大于k时递归, k为指定的数
int pivot = partition(r, low, high); // 调用的Partition算法保持不变
qsort_improve(r, low, pivot - 1,k);
qsort_improve(r, pivot + 1, high,k);
}
}
void quickSort(int r[], int n, int k){
qsort_improve(r,0,n,k);//先调用改进算法Qsort使之基本有序
//再用插入排序对基本有序序列排序
for(int i=1; i<=n;i ++){
int tmp = r[i];
int j=i-1;
while(tmp < r[j]){
r[j+1]=r[j]; j=j-1;
}
r[j+1] = tmp;
}
}
int main(){
int a[10] = {3,1,5,7,2,4,9,6,10,8};
cout<<"初始值:";
print(a,10);
quickSort(a,9,4);
cout<<"结果:";
print(a,10);
}