本题 题目链接
题目描述
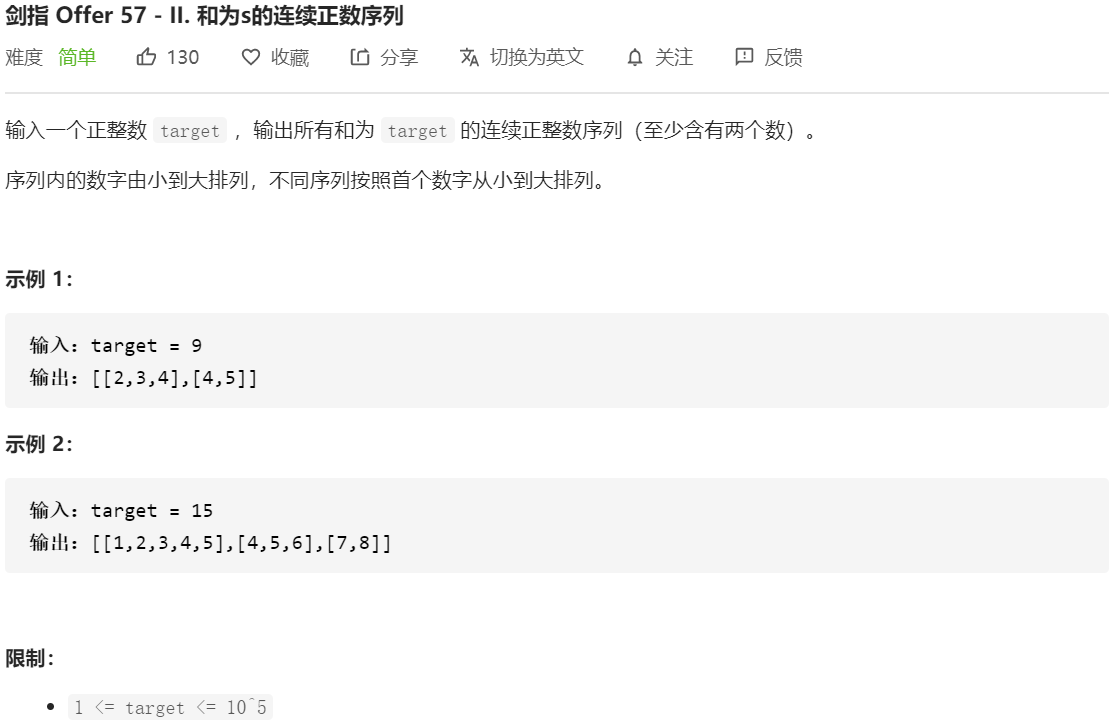
我的题解
方法三双100%, 方法一 适合范围广
方法一:双指针(也叫 滑动窗口)

思路分析
- 用两个指针i和表示当前枚举到的以i为起点,j为终点的区间,sum表示[i,j]的区间和:
- 当sum < tiarget,j指针向前移动,扩大区间,增大区间和。即:j++,sum+=j ;
- 当sum > target,i指针向前移动,收缩区间,减小区间和。即:sum-=i,i++;
- 当sum == target,i指针向前移动2个单位,j向前移动一个单位。即sum = sum-i-(i+1),i-=2,j++,sum+=j;
(当sum=target时,无论是 i 先向前移动,还是 j 先向前移动,另一个指针下一步都会向前一步,此时,一定有sum>target(剔除一个小的加进来一个大的数)。
故而可以直接把 i++和 j++合成一步。又因sum>target,i 又会向前一步。故最终可以再把这两步合成一步,直接令sum=target时,i 向前移动两个单位而j向前移动1个单位)
- (对于求区间和sum也可以用数学公式求啦:(连续序列和=(首项+末项)*项数/2))
代码如下
public int[][] findContinuousSequence(int target) {
ArrayList<int[]> resLists = new ArrayList<>();
int sum = 1;
for (int i = 1,j = 1; j <= (target >>1) + 1; ) {
if (sum < target) {
j++;
sum += j;
} else if (sum > target) {
sum -= i;
i++;
} else {
resLists.add(getArray(i,j));
j++;
sum = sum + j - i - (i + 1);
i = i+2;
}
}
return resLists.toArray(new int[0][]);
}
private int[] getArray(int i, int j) {
if (i == j) return new int[0]; // 题目要求至少含2个数
int[] arr = new int[(j - i + 1)];
for (int k = 0; k <= j - i; k++) arr[k] = k + i;
return arr;
}
方法二:求根公式
(官方的题解,我就不写了,直接截图附上C++代码)

代码如下(C++)
class Solution {
public:
vector<vector<int>> findContinuousSequence(int target) {
vector<vector<int>> vec;
vector<int> res;
int sum = 0, limit = (target - 1) / 2; // (target - 1) / 2 等效于 target / 2 下取整
for (int x = 1; x <= limit; ++x) {
long long delta = 1 - 4 * (x - 1ll * x * x - 2 * target);
if (delta < 0) continue;
int delta_sqrt = (int)sqrt(delta + 0.5);
if (1ll * delta_sqrt * delta_sqrt == delta && (delta_sqrt - 1) % 2 == 0){
int y = (-1 + delta_sqrt) / 2; // 另一个解(-1-delta_sqrt)/2必然小于0,不用考虑
if (x < y) {
res.clear();
for (int i = x; i <= y; ++i) res.emplace_back(i);
vec.emplace_back(res);
}
}
}
return vec;
}
};
方法三:等差数列特殊性质,奇偶讨论,双100
(参考了一位大佬的)

思路分析
-
实际上某个序列可以按其包含奇数/偶数个元素来讨论
- 当某序列含有奇数个(2k+1)元素时,Sequence : i, i+1, i+2 ... i+2k
其序列和为中间元素的2k+1倍,即:Sum(Sequence) = (2k+1) * (i+k) - 当某序列含有偶数个(2k)元素时, Sequence : i, i+1, i+2 ... i+2k-1
其序列和为中间两个元素的k倍,即:Sum(Sequence) = k * [(i+k-1) + (i+k)]
- 当某序列含有奇数个(2k+1)元素时,Sequence : i, i+1, i+2 ... i+2k
-
因此枚举所有可能的序列长度len(从2开始,题目要求至少2个连续的数):
- 奇数时直接判断长度len是否整除target,整除则符合题意,找到序列
- 偶数时判断 2k*(mid1+mid2) = target,k为正整数,mid1和mid2为序列中间的两个数,因连续,故和为大于1的奇数。
成立,则找到序列
-
由于枚举按照序列长度递增顺序,因此输出时将结果逆序输出
-
对于枚举长度,len上界:

代码如下
public int[][] findContinuousSequence(int target) {
ArrayList<int[]> resLists = new ArrayList<>();
int len = 2;
while (len * (1 + len) < (target << 1)) {
if (len % 2 == 1) { // 长度为奇数
if (target % len == 0) { // 找到序列(中间数为 target/len)
int[] arr = new int[len];
for (int i = 0, val = target / len - len / 2; i < len; i++) // 存数组
arr[i] = val++;
resLists.add(arr);
}
} else { // 长度为偶数
int k = len / 2;
// 符合式子: 2k*(mid1+mid2) = target,k为正整数,mid1和mid2为连续的两个数,故和为大于1的奇数
if (target % k == 0 && target / k % 2 == 1) { // 找到序列(中间两个数的和为 target/k)
int[] arr = new int[len];
for (int i = 0, val = target / k / 2 - len / 2 + 1; i < len; i++)
arr[i] = val++;
resLists.add(arr);
}
}
len++;
}
Collections.reverse(resLists);
return resLists.toArray(new int[0][]);
}