原论文:
http://papers.nips.cc/paper/6907-lightgbm-a-highly-efficient-gradient-boosting-decision-tree.pdf
lightgbm原理:
gbdt困点:
gbdt是受欢迎的机器学习算法,当特征维度很高或数据量很大时,有效性和可拓展性没法满足。lightgbm提出GOSS(Gradient-based One-Side Sampling)和EFB(Exclusive Feature Bundling)进行改进。lightgbm与传统的gbdt在达到相同的精确度时,快20倍。
Gradient-based One-Side Sampling (Goss):在GBDT中,数据集没有权重,注意到让不同梯度的数据集在计算信息增益时产生不同的作用。根据信息增益的定义,对于有更大梯度(即训练不足的数据集)将产生更多信息增益。于是,当降低数据集的数据量时,通过保持大梯度的数据集,随机丢掉小梯度的数据集,保持信息增益的准确性。
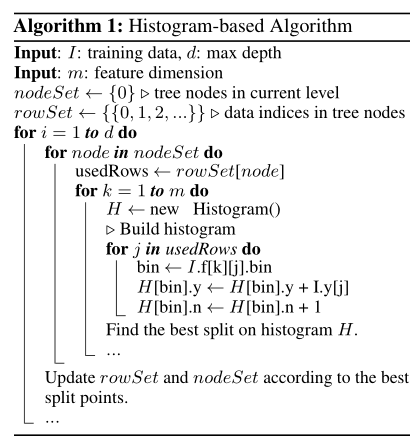

GOSS保持所有具有大梯度的数据集,在小梯度数据集上随机采样。为了抵消对数据分布的影响,GOSS小梯度的样本数据在计算信息增益时引入系数(1-a)/b。具体来说,
- GOSS首先按照数据集的梯度绝对值进行排序,选取最大的a*100%数据集保留;
- 然后从剩余数据集中随机选取b*100%;
- 最后,GOSS对于小梯度乘以常数(1-a)/b放大了样本数据。这样做,我们能不改变原始数据的分布,集中注意力在训练不足的数据上。
收敛分析表明,GOSS算法不会太多降低训练复杂度,并且超越随机选样本。
Exclusive Feature Bundling(EFB). 高维数据通常非常稀疏。特征空间的稀疏性为我们提供了一个设计一种几乎无损的方法来减少特征数量的可能性。具体地说,在一个稀疏的特征空间,许多特征是互斥的,即,它们从不同时取非零值。我们可以安全地将互斥特征捆绑到一个单一的特征中(称之为互斥特征束)。通过精心设计的特征扫描算法,我们可以构建与个体特征类似的基于特征束的特征直方图。这样,直方图构建的复杂性从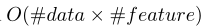 到
到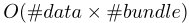 ,其中
,其中 。这样我们可以在不影响准确性情况下大大加快对GBDT的训练。
。这样我们可以在不影响准确性情况下大大加快对GBDT的训练。
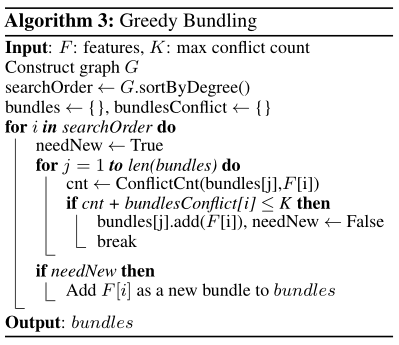

我们的问题对应于图着色问题,反之亦然,因此可以使用贪婪算法来解决。
EFB算法可以将许多互斥性特征捆绑到更少的密集特征上,这可以有效避免了零特征值的不必要计算。事实上,我们也可以通过忽略零特征值,使用表格记录特征非零值的直方图算法。通过扫描表中的数据,直方图构建成本将从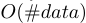 变为
变为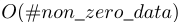 。然而,该方法在树生长过程中需要额外的内存和计算成本来维护这些特征表。我们可以以LightGBM为基本函数按此进行优化。注:这种优化不与EFB冲突,因为我们在捆束稀疏时,依然可以使用它。
。然而,该方法在树生长过程中需要额外的内存和计算成本来维护这些特征表。我们可以以LightGBM为基本函数按此进行优化。注:这种优化不与EFB冲突,因为我们在捆束稀疏时,依然可以使用它。
EFB合并了许多稀疏特征(包括编码特性和隐式互斥性特征),成为少得多的特征。在捆绑过程中包含了基本稀疏特征优化。然而,EFB在树学习过程中为每个特征维护非零数据表,没有额外的成本。更重要的是,因为许多先前孤立的特征被捆绑在一起,它可以增加空间局部性和显著改进缓存命中率。因此,整体效率的提高是引人注目的。以上分析表明,EFB是一种非常有效的在直方图中利用稀疏属性的算法,可以为GBDT训练过程带来显著的加速。
python代码:
import lightgbm
clf=lightgbm
train_matrix = clf.Dataset(tr_x, label=tr_y)
test_matrix = clf.Dataset(te_x, label=te_y)
#z = clf.Dataset(test_x, label=te_y)
#z=test_x
params = {
# 'boosting_type': 'gbdt',
# 'learning_rate': 0.01,
# 'objective': 'binary',
# 'metric': 'auc',
# 'min_child_weight': 1.5,
# 'num_leaves': 2 ** 5,
# 'lambda_l2': 10,
# 'subsample': 0.9,
# 'colsample_bytree': 0.7,
# 'colsample_bylevel': 0.7,
# 'learning_rate': 0.01,
# 'seed': 2017,
# 'nthread': 12,
# 'silent': True,
'task': 'train',
'learning_rate': 0.005,
# 'max_depth': 8,
# 'num_leaves':2**6-1,
'boosting_type': 'gbdt',
'objective': 'binary',
# 'is_unbalance':True,
'feature_fraction': 0.8,
'metric':'auc',
'bagging_fraction': 0.86,
# 'lambda_l1': 0.0001,
'lambda_l2': 49,
'bagging_freq':3,
# 'min_data_in_leaf':5,
'verbose': 1,
'random_state': 2267,
}
num_round = 10000
early_stopping_rounds = 300
if test_matrix:
model = clf.train(params, train_matrix,num_round,valid_sets=test_matrix,
early_stopping_rounds=early_stopping_rounds,verbose_eval=300
)
pre= model.predict(te_x,num_iteration=model.best_iteration).reshape((te_x.shape[0],1))
train[test_index]=pre
test_pre[i, :]= model.predict(test_x, num_iteration=model.best_iteration).reshape((test_x.shape[0],1))
cv_scores.append(roc_auc_score(te_y, pre))