秋招已过，各大厂的面试题分享一波 附C++实现

　　数据结构和算法是面试的一座大山，尤其去面试大厂更是必不可少！简单说明一下为啥喜欢考数据结构和算法，首先，算法有用也没用，如果是中小型企业的简单业务逻辑，可能用不到啥算法，但大厂一定会用到，都知道数据库底层会用到红黑树、B++树等，去oracle公司，那数据结构一定要玩转，再加入想去阿里，百万数据量，不会算法去优化，可能阿里早倒闭，但小长数据量会比较少，用算法就没什么必要了。

　　一、桶排序应用-求最大差值

　　1、题目　　　

　　给定一个数组，求如果排序之后，相邻两数的最大差值，要求时间复杂度O（N），且要求不能用基于比较的排序。

　　2、思路分析　　

　　桶排序应该都知道吧，跟计数排序和基数排序都是非比较排序，像快排、归并都是比较排序。其实，桶排序是一种思想，具体实现是计数排序和基数排序。

接下来直接来分析题目，如下：　　　　

如果有N个数，准备N+1个桶，

遍历找到最小值和最大值

假如，有9个数，准备10个桶，中间必定存在最少一个空桶，说明最大差值一定不在一个桶内，但不一定在空桶两边。

举例子如下：

三个数，四个桶，最大差值19

19  空桶  30   49 

　　3、代码实现

　　如下：

　　

#include<iostream>
#include<vector>
#include<climits>
using namespace std;

class Solution{
    public:
        int maxGap(vector<int> &nums){
            if(nums.size() < 2)
                return 0;

            int len = nums.size();
            int min_index = INT_MAX;
            int max_index = INT_MIN;

            //找出数组的最大值和最小值
            for(int i=0;i<nums.size();i++){
                min_index = min(min_index,nums[i]);
                max_index = max(max_index,nums[i]);
            }
            if(min_index == max_index)
                return 0;
            
            bool *hasNum = new bool[len+1]; //每个桶是否被访问过
            int *maxs = new int[len+1]; //最大值数组
            int *mins = new int[len+1]; //最小值数组

            int bid = 0;
            for(int i = 0;i<len;i++){
                bid = bucket(nums[i],len,min_index,max_index);  //形成桶
                mins[bid] = hasNum[bid] ? min(mins[bid],nums[i]) : nums[i]; //给最大值桶赋值
                maxs[bid] = hasNum[bid] ? max(maxs[bid],nums[i]) : nums[i] ;    //给最小值桶赋值 
                hasNum[bid] = true;
            }
            
            int res = 0;
            int lastMax = maxs[0];
            for(int i=1;i<len;i++){
                if(hasNum[i]){
                    res = max(res,mins[i]-lastMax);
                    lastMax = maxs[i];
                }
            }
            
            return res;
        }
    private:
        int bucket(int num,int len,int min1,int max1){
        return (int) ((num-min1)*len/(max1-min1));
        }
};

int main()
{
    int temp[] = {11,2,44,50,67};
    vector<int> nums(temp,temp+5);
    cout << "max:" << Solution().maxGap(nums) << endl;

    return 0;
}

　　二、用数据实现固定大小的队列和栈

　　1、题目

　　用数据实现固定大小的队列和栈

　　2、思路分析

　　队列和和栈的特性分别是：先进先出和先进后出，思路分析见下图：

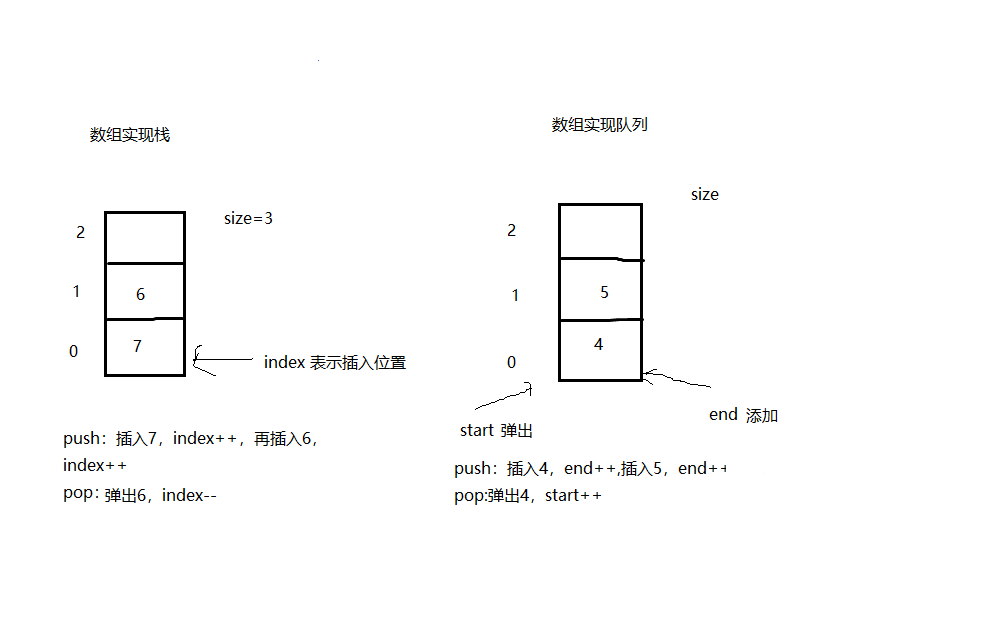
　　图上，标注的很明白了，有不明白的欢迎留言

　　3、代码实现

　　首先是数组实现栈，代码如下：

　　

#include<iostream>
#include<vector>
using namespace std;

class ArrayStack{
    private:
        int index;  //插入位置的下标
        int *arr;
        int maxSize;

    public:
        ArrayStack(int initSize){
            if(initSize < 0)
                throw "The initSize is less than 0";
            arr = new int[initSize];
            index = 0;
            maxSize = initSize;
        }

        void push(int num){ //压入栈
            if(index == maxSize)
                throw "The stack is full";
            arr[index++] = num;
        }
        int pop(){
            if(index == 0)
                throw "The stack is empty";
            return arr[--index];
        }
};

int main()
{
    ArrayStack stack1 = ArrayStack(3);
    stack1.push(2);
    stack1.push(3);
    stack1.push(1);
    cout << "num:" << stack1.pop() << endl;

    return 0;
}

　　用数组实现队列，代码如下：

　　

#include<iostream>
#include<vector>
using namespace std;

class ArrayQueue{
    private:
        int *arr;
        int size;   
        int start;  //弹出下标
        int end;    //插入下标
        int maxSize;    //数组最大值
    public:
        ArrayQueue(int initSize)
        {
            if(initSize < 0)
                throw "The initSize is less than 0";

            arr = new int[initSize];
            size = 0;
            start = 0;
            end = 0;
            maxSize = initSize;
        }

        void push(int num){
            if(size == maxSize)
                throw "the queue is full";
            size++;
            arr[end] = num;
            end = end==maxSize-1?0:end+1;   //让end可以在数组中循环跑
        }
        int pop(){
            if(0 == size)
                throw "the queue is empty";
            size--;
            int tmp = start;
            start = start==maxSize-1?0:start+1; //跟end一样在数组中循环跑
            return arr[tmp];
        }

};

int main()
{
    ArrayQueue arrQueue = ArrayQueue(3);
    arrQueue.push(1);
    arrQueue.push(2);
    cout << "num:" << arrQueue.pop() << endl;

    return 0;
}

　　三、实现特殊的栈 O(1)返回最小元素

　　1、题目

　　实现一个特殊的栈，在实现栈的基本功能上，再实现返回栈中最小元素的操作。

　　【要求】

1. pop、push和getMin操作的时间复杂度都是O(1)
2. 设计的栈类型可以使用现成的栈结构

　　2、思路

直接上图，如下：

　　

　　3、代码实现

　　代码如下：

　　

#include<iostream>
#include<vector>
#include<stack>
using namespace std;

class GetMinStack{
    private:
        stack<int> stackData;
        stack<int> stackMin;
    public:          
        void push(int num){
            if(stackMin.empty()){
                stackMin.push(num);
            }else if(num <= getmin()){
                stackMin.push(num);
            }
            stackData.push(num);


        }

        int pop(){
            if(stackData.empty())
                throw "the empty";
            int value = stackData.top();
            stackData.pop();
            if(value == getmin()){
                stackMin.pop();
            }
            return value;

        }
        
        int getMin(){   //获取最小值
            if(stackMin.empty())
                throw "the stackMin is empty";
            return stackMin.top();
        }

        int getmin(){
            if(stackMin.empty())
                throw "the stack is empty";
            return stackMin.top();
        }

};

int main()
{
    GetMinStack minStack = GetMinStack();
    minStack.push(1);
    minStack.push(3);
    minStack.push(2);
    cout << "pop num:" << minStack.pop() << endl;
    cout << "min num:" << minStack.getMin() << endl;
        

    return 0;
}

　　

　　会继续分享面经和算法，希望持续关注！