一、红黑树特性
1、所有节点不是黑色就是红色。
2、根节点为黑色。
3、null节点为黑色,区别于叶子节点。
4、如果当前节点为红色节点,孩子则全为黑色节点(反之不然)。
5、任意节点到叶子节点的所有路径都包含相同的黑色节点(保持平衡的重要原因)。
三、红黑树修正方式
1、染色:为了符合红黑树的规则特性而改变当前节点的颜色。
2、旋转 :平衡二叉树的操作共性
(1)左旋
演示:
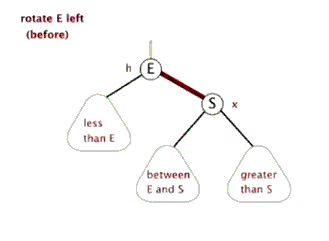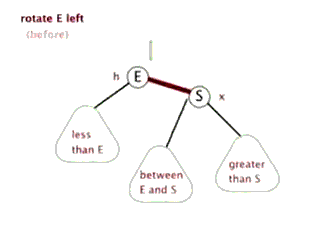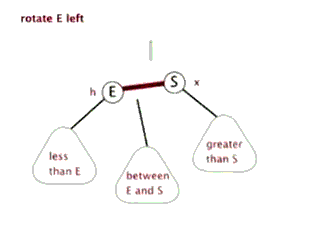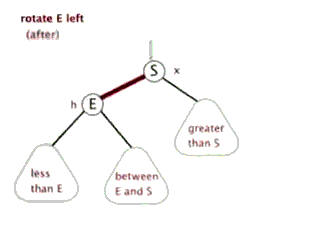
代码:
public void leftRotate(RBNode<T> x){ if(x==null) return; RBNode<T> y = x.right; x.right = y.left; if(y.right!=null){ y.right.parent = x; } y.parent = x.parent; if(x.parent==null){ mRoot = y; }else{ if(x==x.parent.left){ x.parent.left = y; }else{ x.parent.right = y; } } //设置x与y之间的关系 x.parent = y; y.left = x; }
(2)右旋
演示:
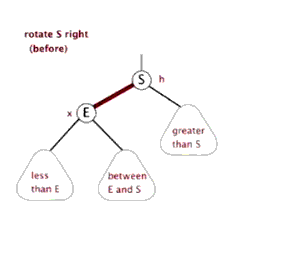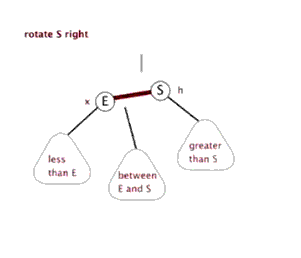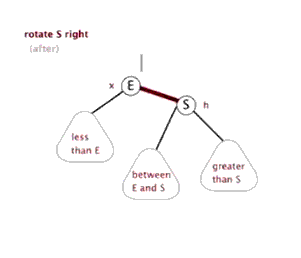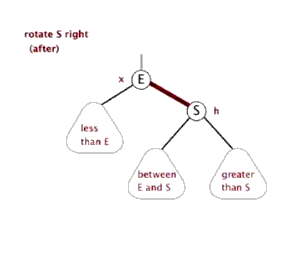
代码:
1 public void rightRotate(RBNode<T> x){ 2 if(x==null) return; 3 4 RBNode<T> y = x.left; 5 x.left = y.right; 6 if(y.right!=null){ 7 y.right.parent = x; 8 } 9 y.parent = x.parent; 10 if(x.parent==null){ 11 mRoot = y; 12 }else{ 13 if(x==x.parent.left){ 14 x.parent.left = y; 15 }else{ 16 x.parent.right = y; 17 } 18 } 19 x.parent = y; 20 y.right = x; 21 }
四、红黑树插入节点
步骤:1、按照二叉树的插入规则插入节点(节点为红色)。2、修正红黑树。
插入节点为红色:插入黑色节点,一定破坏红黑树结构(特性5)。插入红色节点,可能破坏特性(2,4)
情况分析
分析插入节点的父节点为祖父节点的左孩子,如果插入节点的父节点为祖父节点的右孩子则为镜像操作。
核心步骤:看父亲节点,看叔叔节点,看插入位置。
*如果插入红色节点的父节点为黑色,树不需要调整。
*如果插入红色节点的父节点为红色,树需要调整。
(1)叔叔节点为红色。
(2)叔叔节点为黑色,添加节点为父亲节点的左孩子。
(3)叔叔节点为黑色,添加节点为父亲节点的右孩子。
case1:父亲节点为红色,叔叔节点也为红色:
上边的目标节点为左孩子,下边的目标节点为右孩子。

解释:
*将父节点和叔叔节点全部染成黑色(节点T满足了特性四),但是这样父亲和叔叔节点的分支都多了一个黑色;
*将祖父节点染成红色,这样祖父节点的两个分支满足了所有特性,但是我们需要检验祖父节点是否符合红黑树的特性;
*将祖父节点当做插入节点,向根节点进行回溯修改。
停止条件:一直向上回溯,直到父节点变为黑色,或者达到树根为止。
case2:父亲节点为红色,叔叔节点为黑色,插入节点为父亲节点的左孩子。
修正过程:
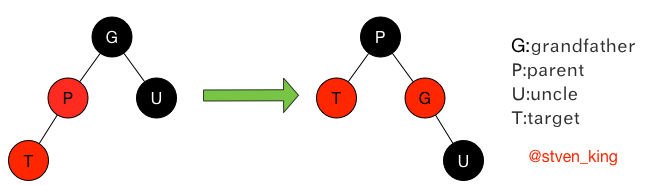
解释:
(1)将父亲节点染成黑色。
(2)将祖父节点染成红色。
(3)对祖父节点进行右旋。
case3:父亲节点为红色,叔叔节点为黑色,插入节点为父亲节点的右孩子。
修正过程:
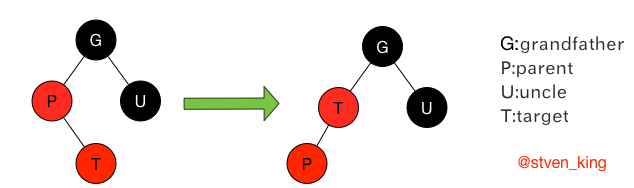
解释:
(1)对父节点进行左旋操作、
(2)将父节点当做插入节点,执行case2情况的红黑树修正。
五、红黑树删除节点
1、平衡二叉树操作方式删除节点
删除case:
(1)待删节点为叶子节点,直接删除。
(2)待删节点只存在一个孩子,使用孩子替换待删节点。
(3)待删节点存在左右孩子,使用中序遍历结果中的后继节点替换待删节点(实际回到了case2)。
删除节点时重点:
case1:直接解除待删节点与父节点之间的关系。
case2:建立待删节点的父节点与替换节点的关系。
case3:1、建立待删节点的父节点与替换节点的关系;2、建立替换节点的父节点与替换节点子节点之间的关系;3、建立替换节点与待删节点的子节点之间的关系。
2、红黑树修正:分析父节点为祖父节点的左孩子,右孩子则为镜像操作。
当删除节点为黑色,需要修正红黑树。
删除节点判断:删除情况的case1和case,删除节点为实际被删节点。删除情况的case3,删除节点为替换节点(因为替换节点被移动到被删节点的位置,并染成与实际被删节点相同的颜色)。
核心思想:从兄弟节点借调黑色节点。
case1:被删节点为黑色节点,兄弟节点为红色
修正过程:
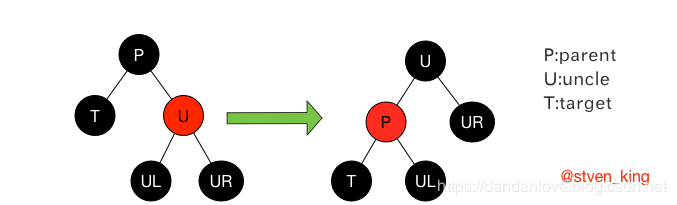
解释:
*将父节点涂红,将兄弟节点涂黑,然后将当前节点的父节点进行支点左旋。这样就转换为兄弟节点为黑色的情况
case2:当前节点为黑色,兄弟节点为黑色,兄弟节点的左右孩子都为黑色
修成过程:
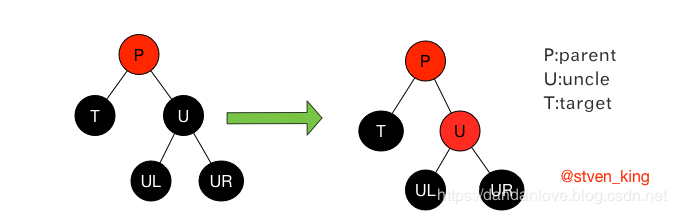
解释:
*将兄弟节点涂红,将当前节点指向其父节点,将其父节点指向当前节点的祖父节点,继续往树根递归判断以及调整;
case3:当前节点为黑色,兄弟节点为红色,近侄子为红色(兄弟节点的左孩子),远侄子为黑色(兄弟节点的右孩子)
修正过程:

解释:
*把当前节点的兄弟节点涂红,把兄弟节点的左子节点涂黑,然后以兄弟节点作为支点做右旋操作。
case4:当前节点为黑色节点,兄弟节点为黑色,近侄子为任意色(兄弟节点的左孩子),远侄子为红色(兄弟节点的右孩子)
修正过程:
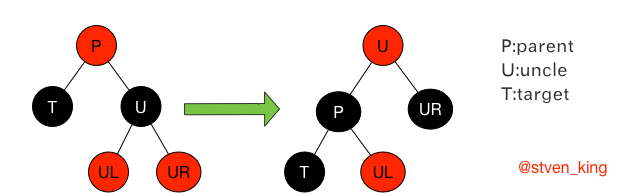
解释:
*把兄弟节点涂成父节点的颜色,再把父节点涂黑,把兄弟节点的右子节点涂黑,然后以当前节点的父节点为支点做左旋操作。
六、红黑树完整代码(java实现)

1 package RBTree; 2 3 /** 4 * 红黑树演示 5 * @param <T> 6 */ 7 public class RBTree<T extends Comparable<T>> { 8 9 public RBNode<T> mRoot = null; 10 public static boolean RED = true; 11 public static boolean BLACK = false; 12 //节点结构 13 class RBNode<T extends Comparable<T>>{ 14 boolean color; 15 T key; 16 RBNode<T> right; 17 RBNode<T> left; 18 RBNode<T> parent; 19 20 public RBNode(boolean color, T key, RBNode<T> right, RBNode<T> left, RBNode<T> parent) { 21 this.color = color; 22 this.key = key; 23 this.right = right; 24 this.left = left; 25 this.parent = parent; 26 } 27 public T getKey(){ 28 return this.key; 29 } 30 31 public boolean getColor(){ 32 return this.color; 33 } 34 @Override 35 public String toString() { 36 return "RBNode{" + 37 "color=" + color + 38 ", key=" + key + 39 ", right=" + right + 40 ", left=" + left + 41 ", parent=" + parent + 42 '}'; 43 } 44 } 45 46 /** 47 * 左旋:设父节点x,x的左子节点y 48 * 1、 49 * @param x 50 */ 51 public void leftRotate(RBNode<T> x){ 52 if(x==null) return; 53 54 RBNode<T> y = x.right; 55 x.right = y.left; 56 if(y.right!=null){ 57 y.right.parent = x; 58 } 59 60 y.parent = x.parent; 61 if(x.parent==null){ 62 mRoot = y; 63 }else{ 64 if(x==x.parent.left){ 65 x.parent.left = y; 66 }else{ 67 x.parent.right = y; 68 } 69 } 70 //设置x与y之间的关系 71 x.parent = y; 72 y.left = x; 73 74 } 75 76 /** 77 * 右旋:左旋的镜像 78 * @param x 79 */ 80 public void rightRotate(RBNode<T> x){ 81 if(x==null) return; 82 83 RBNode<T> y = x.left; 84 x.left = y.right; 85 if(y.right!=null){ 86 y.right.parent = x; 87 } 88 y.parent = x.parent; 89 if(x.parent==null){ 90 mRoot = y; 91 }else{ 92 if(x==x.parent.left){ 93 x.parent.left = y; 94 }else{ 95 x.parent.right = y; 96 } 97 } 98 x.parent = y; 99 y.right = x; 100 } 101 102 public boolean isRED(RBNode<T> node){ 103 return node!=null&&node.getColor(); 104 } 105 /** 106 * 插入节点接口 107 * @param key 108 */ 109 public void insert(T key){ 110 RBNode node = new RBNode<T>(RED,key,null,null,null); 111 insert(node); 112 } 113 114 /** 115 * 在红黑树中插入节点, 116 * 同二叉搜索树的方法相同 117 * @param node 118 */ 119 public void insert(RBNode<T> node){ 120 RBNode<T> k = mRoot; 121 RBNode<T> current = null; 122 //定位 123 while(k!=null){ 124 current = k; 125 int res = node.getKey().compareTo(k.getKey()); 126 if(res<0){ 127 k = k.left; 128 }else{ 129 k = k.right; 130 } 131 } 132 node.parent = current; 133 //插入节点 134 if(current!=null){ 135 int res = node.getKey().compareTo(current.getKey()); 136 if(res<0){ 137 current.left = node; 138 }else{ 139 current.right = node; 140 } 141 insertFixUp(node); 142 }else{ 143 mRoot = node; 144 } 145 } 146 147 /** 148 * 修正插入节点后的红黑树 149 * 如果插入节点的父节点为红色,违背红黑树特性(1、红节点的孩子全为黑节点;2、路径中的黑节点个数)。 150 * case:考虑父节点为祖父节点的左孩子,如果是右孩子则为镜像 151 * 1、父节点的兄弟节点为红色 152 * 2、父节点的兄弟节点为黑色,插入节点左为父节点的左孩子 153 * 3、父节点的兄弟节点为黑色,插入位置作为父节点的右孩子 154 * @param node 155 */ 156 public void insertFixUp(RBNode<T> node){ 157 RBNode<T> parent,gparent; 158 while((parent=node.parent)!=null && isRED(parent)){ 159 gparent = parent.parent; 160 //父节点为祖父节点的左孩子 161 if(parent==gparent.left){ 162 RBNode<T> uncle = gparent.right; 163 //case1:叔叔节点为红色 164 if(uncle!=null && isRED(uncle)){ 165 parent.color = BLACK; 166 uncle.color = BLACK; 167 gparent.color = RED; 168 node = gparent; 169 continue; 170 } 171 //case3:叔叔节点为黑色,插入节点为父节点的右孩子 172 if(node==parent.right){ 173 /* 174 对父节点进行左旋,变成第case2 175 */ 176 leftRotate(parent); 177 //调整父节点与子节点的关系 178 RBNode<T> tmp = parent; 179 parent = node; 180 node = tmp; 181 } 182 //case2:叔叔节点为黑色,插入节点为父节点的左孩子 183 parent.color = BLACK; 184 gparent.color = RED; 185 rightRotate(gparent); 186 }else{ //父节点为祖父节点的右孩子,基本为镜像操作 187 RBNode<T> uncle = gparent.left; 188 189 if(uncle!=null && isRED(uncle)){ 190 uncle.color = BLACK; 191 parent.color = BLACK; 192 gparent.color = RED; 193 node = gparent; 194 continue; 195 } 196 if(node==parent.left){ 197 rightRotate(parent); 198 RBNode<T> tmp = parent; 199 parent = node; 200 node = tmp; 201 } 202 parent.color = BLACK; 203 gparent.color = RED; 204 leftRotate(gparent); 205 } 206 } 207 this.mRoot.color = BLACK; 208 } 209 210 /** 211 * 删除节点 212 * 1、删除节点:保证二叉树规则 213 * 2、调整结构:保证红黑树规则。 214 * (1)删除节点为红色,不需要进行调整 215 * (2)删除节点为黑色,需要进行调整 216 * @param key 217 */ 218 public void remove(T key){ 219 RBNode<T> node; 220 if((node = search(mRoot,key))!=null){ 221 remove(node); 222 } 223 } 224 public void remove(RBNode<T> node){ 225 RBNode<T> child,parent; 226 boolean color; 227 /* 228 待删除节点同时存在左右孩子 229 找到后继节点:中序遍历的下一个节点 230 */ 231 if(node.left!=null && (node.right!=null)){ 232 RBNode<T> replace = node.right; 233 while(replace.left!=null){ 234 replace = replace.left; 235 } 236 //处理待删节点的父节点与后继节点的关系 237 if(node.parent!=null){ 238 if(node==node.parent.left){ 239 node.parent.left = replace; 240 }else{ 241 node.parent.right= replace; 242 } 243 }else{ 244 mRoot = replace; 245 } 246 //建立后继节点的子节点与父节点的关系 247 //后继节点一定不存在左孩子。 248 child = replace.right; 249 parent = replace.parent; 250 color = replace.color; 251 //后继节点的父节点为待删节点 252 if(parent==node){ 253 parent = replace; 254 }else{ 255 if(child!=null){ 256 child.parent = parent; 257 } 258 parent.left = child; 259 //处理后继节点与待删节点的子节点的关系 260 replace.right = node.right; 261 node.right.parent = replace; 262 } 263 replace.parent = node.parent; 264 replace.color = node.color; 265 replace.left = node.left; 266 node.right.parent = replace; 267 if(color == BLACK){ 268 removeFixUp(child,parent); 269 } 270 //删除节点 271 node = null; 272 }else{ 273 //被删除的节点为叶子节点或只有一个孩子 274 if(node.left!=null){ 275 child = node.left; 276 }else{ 277 child = node.right; 278 } 279 parent = node.parent; 280 color = node.color; 281 if(child!=null){ 282 child.parent = parent; 283 } 284 if(parent!=null){ 285 if(node == node.parent.left){ 286 node.parent.left = child; 287 }else{ 288 node.parent.right = child; 289 } 290 }else{ 291 mRoot = child; 292 } 293 if(color == BLACK){ 294 removeFixUp(child,parent); 295 } 296 node = null; 297 } 298 } 299 300 /** 301 * 为了保证删除节点的父节点左右两边黑色节点数一致,需要重点关注父节点没删除的那一边节点是不是黑色。 302 * * 如果删除后父亲节点另一边比删除的一边黑色多,就要想办法搞到平衡。 303 * * 1、把父亲节点另一边(即删除节点的兄弟树)其中一个节点弄成红色,也少了一个黑色。 304 * * 2、或者把另一边多的节点(染成黑色)转过来一个 305 * * 306 * * 1)、当前节点是黑色的,且兄弟节点是红色的(那么父节点和兄弟节点的子节点肯定是黑色的); 307 * * 2)、当前节点是黑色的,且兄弟节点是黑色的,且兄弟节点的两个子节点均为黑色的; 308 * * 3)、当前节点是黑色的,且兄弟节点是黑色的,且兄弟节点的左子节点是红色,右子节点时黑色的; 309 * * 4)、当前节点是黑色的,且兄弟节点是黑色的,且兄弟节点的右子节点是红色,左子节点任意颜色。 310 * @param node 311 * @param parent 312 */ 313 public void removeFixUp(RBNode<T> node,RBNode<T> parent){ 314 RBNode<T> other; 315 RBNode<T> root = mRoot; 316 while((node==null || node.color == BLACK) && node!=root){ 317 if(node == parent.left){ 318 other = parent.right; 319 //case1:兄弟节点为红色 320 if(other!=null && isRED(other)){ 321 other.color = BLACK; 322 parent.color = RED; 323 leftRotate(parent); 324 other = parent.right; 325 } 326 //case2:兄弟节点为黑色,其左右孩子也为黑色。 327 if((other.left == null || other.left.color==BLACK) && 328 (other.right==null || other.right.color==BLACK)){ 329 other.color = RED; 330 node = parent; 331 parent = node.parent; 332 }else{ 333 //case3:兄弟节点为黑色,兄弟节点的左孩子为红色色,右孩子为黑色。 334 if(other.right == null || other.right.color==BLACK){ 335 other.left.color = BLACK; 336 other.color = RED; 337 rightRotate(other); 338 other = parent.right; 339 } 340 //case4:兄弟节点为黑色,且兄弟节点的右孩子红色,左孩子任意颜色 341 other.color = parent.color; 342 parent.color = BLACK; 343 other.right.color = BLACK; 344 leftRotate(parent); 345 node = root; 346 break; 347 } 348 }else{ 349 other = parent.left; 350 if(other!=null && isRED(other)){ 351 other.color = BLACK; 352 parent.color = RED; 353 rightRotate(parent); 354 other = parent.left; 355 } 356 if((other.left==null || other.left.color==BLACK) && 357 (other.right==null || other.right.color==BLACK)){ 358 other.color = RED; 359 node = parent; 360 parent = node.parent; 361 }else{ 362 if(other.left==null || other.left.color==BLACK){ 363 other.right.color = BLACK; 364 other.color = RED; 365 leftRotate(other); 366 other = parent.left; 367 } 368 other.color = parent.color; 369 parent.color = BLACK; 370 other.left.color = BLACK; 371 rightRotate(parent); 372 node = root; 373 break; 374 } 375 } 376 } 377 if(node != null){ 378 node.color = BLACK; 379 } 380 } 381 382 /** 383 * 搜索key 384 * 返回key所在节点 385 * @param key 386 * @return 387 */ 388 public RBNode<T> search(RBNode<T> mRoot,T key){ 389 if(mRoot==null){ 390 return null; 391 } 392 RBNode<T> current = mRoot; 393 while(current!=null){ 394 int res = key.compareTo(current.getKey()); 395 if(res<0){ 396 current = current.left; 397 }else if(res>0){ 398 current = current.right; 399 }else{ 400 //找到节点 401 return current; 402 } 403 } 404 return null; 405 406 } 407 408 }
博客参考:
http://dandanlove.com/2018/03/18/red-black-tree/(基本参考了此博客)
https://zhuanlan.zhihu.com/p/24367771
http://blog.csdn.net/eson_15/article/details/51144079
将将当前节点指向其父节点,将其父节点指向当前节点的祖父节点,继续往树根递归判断以及调整;
