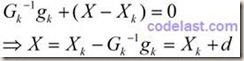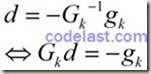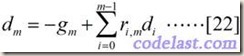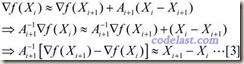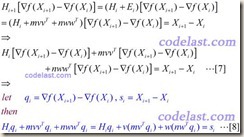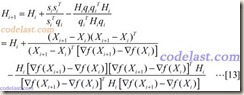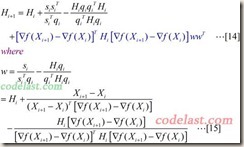最优化之路

进入算法研发部，在大致了解部门的项目构成，主要职责之后，我意识到最优化算法在各个项目组中都具有重要的作用，例如CTR预估、排序等。然而，由于自己在读博期间除了“逻辑回归”以外，没有系统参与过涉及最优化的项目，因此在还没有分配到具体任务的情况下，首先自发地对最优化算法的发展历程进行了调研。心得体会如下：

最优化领域中的方法虽然“多如牛毛”，但是总体上还是沿着一条“主线”发展的。这里按照时间顺序对这条“最优化之路”进行简要介绍：

1.1 最速下降法（梯度法）：

即以负梯度方向作为目标函数极小化方法的下降方向。首先将目标函数进行泰勒展开：

：代表第k个点的自变量（向量）；

:单位方向（向量），即|d|=1；

：步长（实数）；

：目标函数在X_k这一点的梯度（导数向量）；

：α的高阶无穷小。

式[1]中的高阶无穷小可以忽略，因此，要使[1]式取得最小值，应使取到最小，由此可得，取时，目标函数下降得最快，这就是负梯度方向作为“最速下降”方向的由来。

1.2 牛顿法：

最速下降法只用到了目标函数的一阶导数信息，而牛顿法则用到了二阶导数信息。在点处对目标函数进行泰勒展开，并只取二阶导数及其之前的几项（忽略更高阶的导数项），可得：

：目标函数在这一点的梯度；

：目标函数在这一点的Hessian矩阵（二阶导数矩阵）。

由于极小值点必然是驻点，而驻点是一阶导数为0的点，所以，对 r(X) 这个函数来说，要取到极小值，应该分析其一阶导数。对X求一阶导数，并令其等于0：

因此，下一点的计算方法：在方向d上按步长1（1×d = d）移动到点X，方向d的计算方法：

牛顿法的基本步骤：每一步迭代过程中，通过解线性方程组得到搜索方向，然后将自变量移动到下一个点，然后再计算是否符合收敛条件，不符合的话就一直按这个策略（解方程组→得到搜索方向→移动点→检验收敛条件）继续下去。由于牛顿法利用了目标函数的二阶导数信息，其收敛速度为二阶收敛，因此它比最速下降法要快，但是其对一般问题不是整体收敛的，只有当初始点充分接近极小点时，才有很好的收敛性。

1.3 共轭方向法：

最速下降法和牛顿法对前后两次迭代的方向并没有特别的相关要求，而共轭方向法则要求新的搜索方向与前面所有的搜索方向是共轭的。也就是说，这些搜索方向向量是满足以下共轭条件的：

其中，m≠n，dm和dn分别为两个向量（搜索方向），G为对称正定矩阵。共轭方向法只利用了目标函数的一阶导数（梯度）信息，不用计算Hessian矩阵，使得其计算量比牛顿法小很多。在每一步迭代的过程中，可以利用“Powell共轭方向集”方法构造两两共轭的方向。在共轭方向法中，新搜索方向的确定，需要满足“下降”条件，即方向与梯度之积<0：

但是，并不是意味着目标函数值下降量越大，这个方向就越可取。在Powell算法的修正策略中，有一种方法通过放弃目标函数值下降最大的方向而更好地避免了各方向的线性相关。共轭方向法的过程可以总结为：选定搜索方向d，使之满足共轭条件以及下降条件，在此搜索方向上通过精确线性搜索确定移动的步长，然后将当前点移动到下一点，再重新选定搜索方向，周而复始，直到满足终止条件。 共轭方向法的收敛速度比最速下降法快，比牛顿法慢。

1.4 共轭梯度法：

“共轭梯度法”是一种特殊的“共轭方向法”。共轭方向法与梯度的关系是——共轭方向法利用了目标函数的梯度信息（梯度与方向的积满足“下降”条件）。共轭梯度法与此关系有所区别：用当前点的负梯度方向，与前面的搜索方向进行共轭化，以得到新的搜索方向。在推导共轭梯度法的搜索方向的公式之前，我们先假定目标函数是二次函数：

其中G为n阶对称正定矩阵。X为自变量（n维向量）。

[2]式的函数的梯度（即一阶导数）为：

现在，假设初始点为X₀。在每一个迭代点处，新的搜索方向都是用前面的搜索方向与当前点的负梯度方向共轭化得到的。在初始点X₀处，并没有“前面的搜索方向”，因此，初始点处的搜索方向d₀简单地定为负梯度方向：

上面的式子中，将目标函数在X₀点的梯度g(X₀)写为g₀，同理，g(X₁)也记为g₁，等等。

第二个迭代到的点为X1，它与X0满足关系：

这表明，点X₁是在d₀方向上，由X₀点移动一定的距离得到的。移动的步长α₀，则是通过精确线搜索的方法计算得到的，X₁是一个极小值点，在点X₁处，目标函数的一阶导数为零，即：

所以一阶导数再乘以d₀仍然为零：

从共轭梯度法的定义——新的搜索方向是用前面的搜索方向与当前点的负梯度方向共轭化得到的——来看，d₁与d₀（前面的搜索方向）有关，也与-g1（当前点的负梯度方向）有关，因此，假定d₁是-g₁与d₀的线性组合：

其中，r₀是一个实数。此外，由于每一个搜索方向与前面的搜索方向都是共轭的，因此，d₁与d₀还要满足共轭条件：

计算r₀的值:

首先，在同一点处，搜索方向与梯度的点积：

可以看出，在同一点处，搜索方向与梯度的点积等于负梯度与梯度的点积。

其次，在某一点处的梯度与前面所有的梯度的点积：

点X₂，X₃，……均为极小值点，因此，在这些点处，目标函数的梯度为零，即g(X_k)=0，因此[14]，[15]式均为零，得到：

又可以看出，在某一点处的梯度与前面所有梯度的点积为零。

由上面的特例的计算，可以总结出一些规律并用这些规律来得到通用的结论。假设对所有的搜索方向和梯度，有如下规律：

即同一点处的搜索方向与梯度的点积等于该点处的负梯度与梯度的点积，某一点处的梯度与前面所有搜索方向的点积为0，某一点处的梯度与前面所有梯度的点积为0，某一点处的搜索方向与前面所有搜索方向共轭。

设方向d的通用的表达式为：

该式表示的含义是：当前点的搜索方向是当前点的负梯度方向与前面所有方向的线性组合。前文所述的方向d1，也是这样假设之后再求出来的。[22]式的左边是一个方向向量，在共轭梯度法中，要保证某一点的搜索方向与前面所有搜索方向是G共轭的，因此，在[22]式两边均左乘一个式子，形成“G共轭”的表达式：

例如，当m=4时，[22]式就是用来求d₄的，此时：

对n所取的任何值，在[24]式的求和式∑中，除最后一项外，其余所有项的值均为0——这是因为任何一个方向与前面所有方向都是G共轭的（参看G共轭的定义）。所以现在可以写出[24]式的结果了：

完全可以用r_n来代替[25]式中的r的表达式：

[29]式就是r的计算方法。

共轭梯度法同样会有与共轭方向法类似的问题：经过n步迭代之后，产生的新方向不再有共轭性。所以在实际运用中，也有很多修正方向的策略。其中一种策略是：经过n步迭代之后，取负梯度方向作为新的方向。共轭梯度法比最速下降法的收敛性要好得多。

1.5 拟牛顿（Quasi-Newton）法：

拟牛顿法是一种“模拟”的牛顿法，具体来说模拟的是牛顿法中搜索方向的生成方式。牛顿法中，在每一次要得到新的搜索方向的时候，都需要计算Hessian矩阵（二阶导数矩阵）。在自变量维数非常大的时候，这个计算工作是非常耗时的，因此，拟牛顿法的诞生的意义就是：它采用了一定的方法来构造与Hessian矩阵相似的正定矩阵，而这个构造方法计算量比牛顿法小。

1.5.1 DFP算法

假设目标函数可以用二次函数进行近似（实际上很多函数可以用二次函数很好地近似）：

忽略高阶无穷小部分，只看前面3项，其中A为目标函数的Hessian矩阵。此式等号两边对X求导，可得：

于是，当 X=X_i 时，将[2]式两边均左乘A_i+1^-1，有：

上式左右两边近似相等，但如果我们把它换成等号，并且用另一个矩阵H来代替上式中的A^-1，则得到：

方程[4]就是拟牛顿方程，其中的矩阵H，就是Hessian矩阵的逆矩阵的一个近似矩阵.在迭代过程中生成的矩阵序列H0，H1，H2，……中，每一个矩阵H_i+1，都是由前一个矩阵H_i修正得到的。DFP算法的修正方法如下，设：

再设：

其中，m和n均为实数，v和w均为N维向量。将[6]代入[5]式，再将[5]式代入[4]式，可得：

得到的m，n，v，w值如下：

将[8]~[11]代入[6]式，然后再将[6]代入[5]式，就得到了Hessian矩阵的逆矩阵的近似阵H的计算方法：

通过上述描述，DFP算法的流程大致如下：

已知初始正定矩阵H₀，从一个初始点开始（迭代），用式子 来计算出下一个搜索方向，并在该方向上求出可使目标函数极小化的步长α，然后用这个步长，将当前点挪到下一个点上，并检测是否达到了程序终止的条件，如果没有达到，则用上面所说的[13]式的方法计算出下一个修正矩阵H，并计算下一个搜索方向……周而复始，直到达到程序终止条件。

值得注意的是，矩阵H正定是使目标函数值下降的条件，所以，它保持正定性很重要。可以证明，矩阵H保持正定的充分必要条件是：

在迭代过程中，这个条件也是容易满足的。

1.5.2 BFGS算法

BFGS算法和DFP算法有些相似，但是形式上更加复杂一些。BFGS算法目前仍然被认为是最好的拟牛顿算法。BFGS算法中矩阵H的计算公式如下所示：

在[14]式中的最后一项（蓝色部分）就是BFGS比DFP多出来的部分，其中w是一个n×１的向量。

在目标函数为二次型时，无论是DFP还是BFGS——也就是说，无论[14]式中有没有最后一项——它们均可以使矩阵H在n步之内收敛于A^-1。

BFGS算法有一个变种，叫作“Limited-memory BFGS”，简称“L-BFGS”。使用L-BFGS算法来编写程序时，它会比BFGS算法占用的内存小。

另外，还有“面向象限”的OWLQN算法（Orthant-Wise Limited-memory Quai-Newton），这里不再赘述。

以颤抖之身追赶，怀敬畏之心挑战