1. 分类问题
1.1 二分类
-
(f:x ightarrow p(y=1|x))
-
(p(y=1|x)): 解释成给定x,求y=1的概率,如果概率>0.5,预测为1;否则,预测为0
-
(p_{ heta}(y|x)):给定x,输出预测值的概率
-
(p_{r}(y|x)):给定x,真实分布
-
1.2 多分类
-
(f:x ightarrow p(y|x))
- ([p(y=0|x),p(y=1|x),...,p(y=9|x)])
-
(p(y|x)epsilon [0,1])
-
(sum_{i=0}^{9}p(y=i|x)=1)
[p_i = frac{e^{a_i}}{sum_{k=1}^{N} e^{a_k}}
]
2. 交叉熵
2.1 信息熵
- 描述一个随机事件的不确定性。
[H(p)=-sum _{xepsilon X}p(x)logp(x)
]
- 描述一个分布,熵越高,随机变量的信息越多。
import torch
a = torch.full([4],1/4.)
print(-(a*torch.log2(a)).sum()) # tensor(2.)
b = torch.tensor([0.1,0.1,0.1,0.7])
print(-(b*torch.log2(b)).sum()) # tensor(1.3568)
c = b = torch.tensor([0.001,0.001,0.001,0.999])
print(-(c*torch.log2(c)).sum()) # tensor(0.0313)
2.2 交叉熵
- 公式:
[H(p,q)=-sum _{xepsilon X}p(x)logq(x)
]
[H(p)=-sum _{xepsilon X}p(x)logp(x)
]
[D_{KL}(p|q) = H(p,q) - H(p)
]
-
KL散度 = 交叉熵H(p,q) - 信息熵H(p),用 分布q 来模拟 真实分布p 所需的额外信息。
-
p = q,H(p,q) = H(p)
-
对one-hot Encoding来说,entropy = H(p) = 1log1 = 0
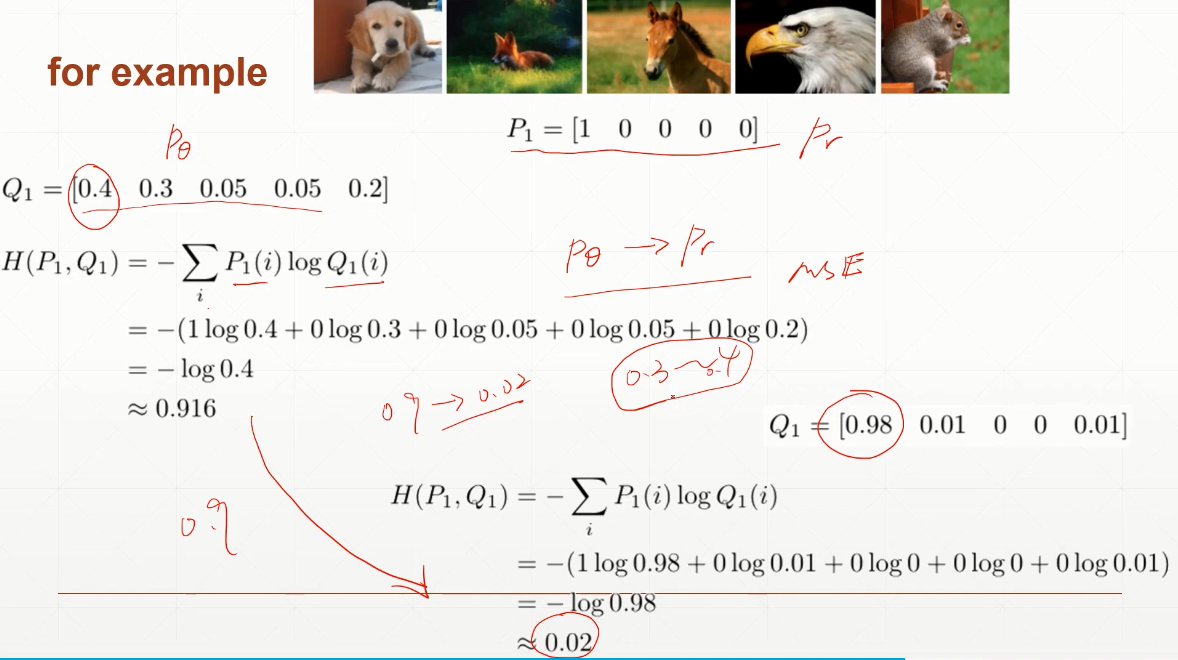
2.3 二分类问题的交叉熵
- P(i)指i的真实值,Q(i)指i的预测值。
(H(p, q) = -sum _{iepsilon cat,dog}P(i)logQ(i))
(H(p, q) = -P(cat)logQ(cat) - P(dog)logQ(dog))
(H(p, q) = -sum _{i=1}^{n}y_ilog(p_i)+(1-y_i)log(1-p_i))
import torch
from torch.nn import functional as F
x = torch.randn(1,784)
w = torch.randn(10,784)
logits = x@w.t() # shape=torch.Size([1,10])
# 方法1:推荐
# pytorch中cross_entropy已经经过了softma+log+nll_loss,所以这里传入logits
# 参数: (predict, label)
print(F.cross_entropy(logits, torch.tensor([3]))) # tensor(77.1405)
# 方法2:容易计算错
# 如果一定要自己计算softmax+log
pred = F.softmax(logits,dim=1) # shape=torch.Size([1,10])
pred_log = torch.log(pred)
print(F.nll_loss(pred_log, torch.tensor([3]))) # tensor(77.1405)
3. 多分类实战
- 识别手写数据集
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
#超参数
batch_size=200
learning_rate=0.01
epochs=10
#获取训练集
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True, #train=True则得到的是训练集
transform=transforms.Compose([ #transform进行数据预处理
transforms.ToTensor(), #转成Tensor类型的数据
transforms.Normalize((0.1307,), (0.3081,)) #进行数据标准化(减去均值除以方差)
])),
batch_size=batch_size, shuffle=True) #按batch_size分出一个batch维度在最前面,shuffle=True打乱顺序
#获取测试集
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
#设定参数w和b
w1, b1 = torch.randn(200, 784, requires_grad=True),
torch.zeros(200, requires_grad=True) #w1(out,in)
w2, b2 = torch.randn(200, 200, requires_grad=True),
torch.zeros(200, requires_grad=True)
w3, b3 = torch.randn(10, 200, requires_grad=True),
torch.zeros(10, requires_grad=True)
torch.nn.init.kaiming_normal_(w1)
torch.nn.init.kaiming_normal_(w2)
torch.nn.init.kaiming_normal_(w3)
def forward(x):
x = x@w1.t() + b1
x = F.relu(x)
x = x@w2.t() + b2
x = F.relu(x)
x = x@w3.t() + b3
x = F.relu(x)
return x
#定义sgd优化器,指明优化参数、学习率
optimizer = optim.SGD([w1, b1, w2, b2, w3, b3], lr=learning_rate)
criteon = nn.CrossEntropyLoss()
for epoch in range(epochs):
for batch_idx, (data, target) in enumerate(train_loader):
data = data.view(-1, 28*28) #将二维的图片数据摊平[样本数,784]
logits = forward(data) #前向传播
loss = criteon(logits, target) #nn.CrossEntropyLoss()自带Softmax
optimizer.zero_grad() #梯度信息清空
loss.backward() #反向传播获取梯度
optimizer.step() #优化器更新
if batch_idx % 100 == 0: #每100个batch输出一次信息
print('Train Epoch: {} [{}/{} ({:.0f}%)] Loss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
test_loss = 0
correct = 0 #correct记录正确分类的样本数
for data, target in test_loader:
data = data.view(-1, 28 * 28)
logits = forward(data)
test_loss += criteon(logits, target).item() #其实就是criteon(logits, target)的值,标量
pred = logits.data.max(dim=1)[1] #也可以写成pred=logits.argmax(dim=1)
correct += pred.eq(target.data).sum()
test_loss /= len(test_loader.dataset)
print('
Test set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)
'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
view result
Train Epoch: 0 [0/60000 (0%)] Loss: 2.551489
Train Epoch: 0 [20000/60000 (33%)] Loss: 0.937205
Train Epoch: 0 [40000/60000 (67%)] Loss: 0.664578
Test set: Average loss: 0.0030, Accuracy: 8060/10000 (81%)
Train Epoch: 1 [0/60000 (0%)] Loss: 0.594552
Train Epoch: 1 [20000/60000 (33%)] Loss: 0.534821
Train Epoch: 1 [40000/60000 (67%)] Loss: 0.676503
Test set: Average loss: 0.0026, Accuracy: 8277/10000 (83%)
Train Epoch: 2 [0/60000 (0%)] Loss: 0.393263
Train Epoch: 2 [20000/60000 (33%)] Loss: 0.424480
Train Epoch: 2 [40000/60000 (67%)] Loss: 0.560588
Test set: Average loss: 0.0024, Accuracy: 8359/10000 (84%)
Train Epoch: 3 [0/60000 (0%)] Loss: 0.559309
Train Epoch: 3 [20000/60000 (33%)] Loss: 0.547236
Train Epoch: 3 [40000/60000 (67%)] Loss: 0.537494
Test set: Average loss: 0.0023, Accuracy: 8423/10000 (84%)
Train Epoch: 4 [0/60000 (0%)] Loss: 0.549808
Train Epoch: 4 [20000/60000 (33%)] Loss: 0.405319
Train Epoch: 4 [40000/60000 (67%)] Loss: 0.368419
Test set: Average loss: 0.0022, Accuracy: 8477/10000 (85%)
Train Epoch: 5 [0/60000 (0%)] Loss: 0.371384
Train Epoch: 5 [20000/60000 (33%)] Loss: 0.409493
Train Epoch: 5 [40000/60000 (67%)] Loss: 0.354021
Test set: Average loss: 0.0021, Accuracy: 8523/10000 (85%)
Train Epoch: 6 [0/60000 (0%)] Loss: 0.448938
Train Epoch: 6 [20000/60000 (33%)] Loss: 0.439384
Train Epoch: 6 [40000/60000 (67%)] Loss: 0.476088
Test set: Average loss: 0.0020, Accuracy: 8548/10000 (85%)
Train Epoch: 7 [0/60000 (0%)] Loss: 0.401981
Train Epoch: 7 [20000/60000 (33%)] Loss: 0.405808
Train Epoch: 7 [40000/60000 (67%)] Loss: 0.492355
Test set: Average loss: 0.0020, Accuracy: 8575/10000 (86%)
Train Epoch: 8 [0/60000 (0%)] Loss: 0.385034
Train Epoch: 8 [20000/60000 (33%)] Loss: 0.367822
Train Epoch: 8 [40000/60000 (67%)] Loss: 0.333447
Test set: Average loss: 0.0020, Accuracy: 8593/10000 (86%)
Train Epoch: 9 [0/60000 (0%)] Loss: 0.349438
Train Epoch: 9 [20000/60000 (33%)] Loss: 0.390028
Train Epoch: 9 [40000/60000 (67%)] Loss: 0.390438
Test set: Average loss: 0.0019, Accuracy: 8604/10000 (86%)