要得到某个结果,可以有很多种方式,算法就是为了寻找一条最快的方式。
而评判其好坏的标准就是时间复杂度。
O(1):
我们把执行一次的时间复杂度定义为O(1)
sum = a +b;
cout << sum <<endl;
O(n):
for(int i = 0; i < n ;++n)
{
//do something.
}
O(n2):
for(int i = 0; i < n ;++n)
{
for(int j = 0; j < n ;++n)
{
//do something.
}
}
我们会碰到这样的需求,从一个主字符串中找到一个子串,首先我们想到的是这种方法:
#include "stdafx.h"
#include<iostream>
#include<string>
using namespace std;
int findString(string S,string T)
{
int i = 0;
int j = 0;
while(i<S.length() && j < T.length())
{
if(T[j] == S[i])
{
i++;
j++;
}
else
{
j=0;
i = i-j+1;
}
}
if(j = T.length())
{
return i-j;
}
else
{
return -1;
}
}
void main()
{
int a = findString("adsfdjfxdf","xdf");
cout << a <<endl;
cin.get();
cin.get();
}
时间复杂度为O(n*m)这个好理解,每比较m次,主字符串位置加1,最坏的情况就是比较n*m次
而实际上,我们不需要这样做,例如如果要在主字符串中找abcd,那每次i可以加4,下次直接从第5个开始比较。这样的时间复杂度是O(n/m*m) = O(n),而实际上我们要找的子串有可能会重复,于是一种更通用的算法就产生了, 克努特一莫里斯一普拉特算法, 简称 KMP 算法。
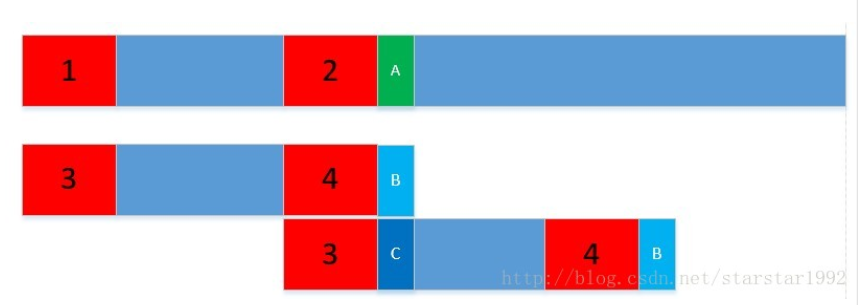
主要思想基于上图,找到的比较便于理解的图,上图中1,2,3,4为相同内容,中间蓝色为相同内容,当我们第一次比较时,发现A和B不同,那么下一次比较时,我们主串仍从A开
始,而子串则从C处开始,3和2相同的内容便不再需要比较。具体解释百度,其实一看就能感觉应该是这样,而i从上次比较失败的地方继续开始在代码上逻辑也不混乱。
因此KMP算法比较关键的便是如何得到子串失败后开始的这个点C,为了得到这个C的位置i,KMP这3个人设计了一个中间数组,来保存子串的若比较失败应该开始的下一个比较点。
next数组, 含义就是一个固定字符串的最长前缀和最长后缀相同的长度。
比如:abcjkdabc,那么这个数组的最长前缀和最长后缀相同必然是abc。
cbcbc,最长前缀和最长后缀相同是cbc。 这个子串的next数组是[0,0,1,2,0]
#include "stdafx.h"
#include<iostream>
#include<string>
using namespace std;
void get_next(string T,int* next)
{
next[0] = -1;
int i = 0;
int j = -1;
while(i<T.length())
{
if((j == (-1)) || (T[i] == T[j]))
{
next[++i] = ++j;
}
else
{
j = next[j]; //可以想象两个子串如上图一样的比较
}
}
}
int KMP(string S , string T)
{
int * next = new int[T.length()+1];
int i = 0;
int j = 0;
get_next(T, next);
while(i < int(S.length()) && j < int(T.length()))
{
if((-1 == j) || S[i] == T[j])
{
i++;
j++;
}
else
{
j=next[j]; //如上图4区域刚好是next[j]不需要比较,从c处开始比较
}
}
delete []next;
if(j == T.length())
{
return i-j;
}
else
{
return -1;
}
}
void main()
{
string S;
string T;
cout<<"please input the Mstring:"<<endl;
cin>>S;
cout<<endl<<"please input the Cstring:"<<endl;
cin >>T;
cout<<S.length()<<endl;
cout<<T.length()<<endl;
cout<<"the child String in the M number is: "<< KMP(S,T);
system("pause");
}
这个时间复杂度是O(m+n),因为是两个单循环相加。
写这个的时候 while(i < int(S.length()) && j < int(T.length())) 这句没有强转化int,导致j = -1时while循环只执行了一次未继续下去,后来看了一下length返回的并不是int,而是一个抽象的size,被这个错误搞得有点心态崩了。
O(1)