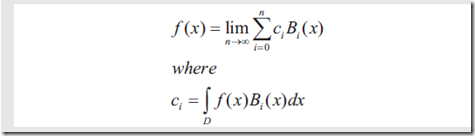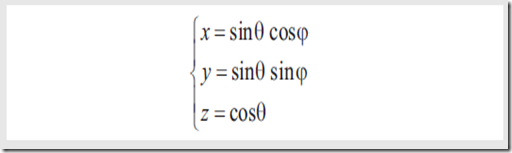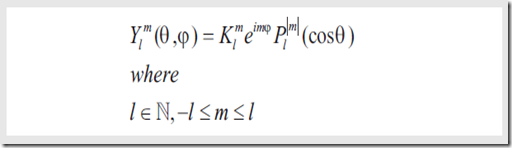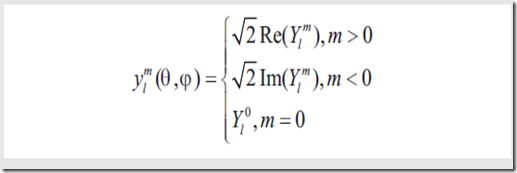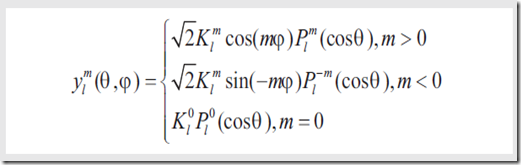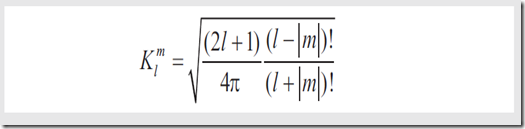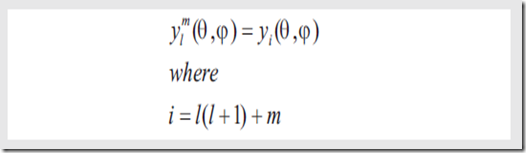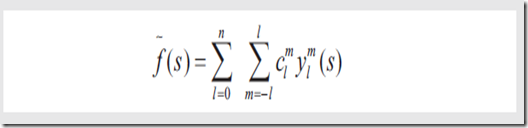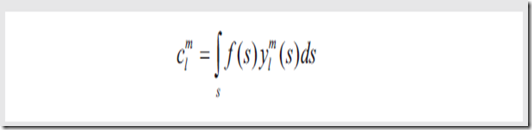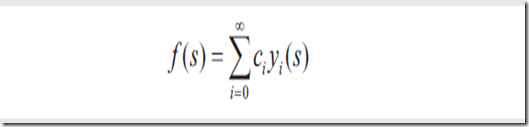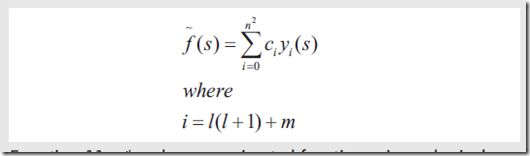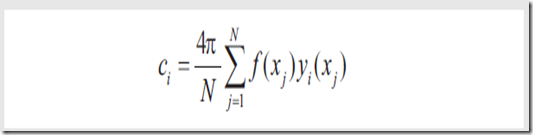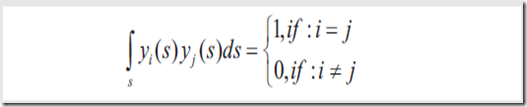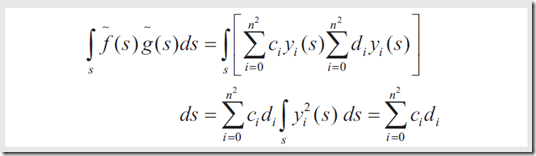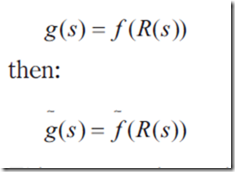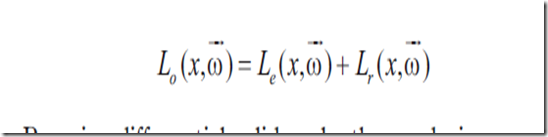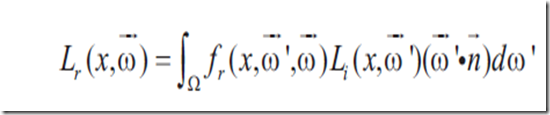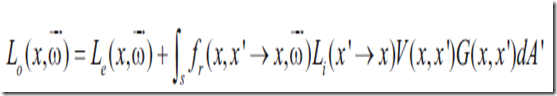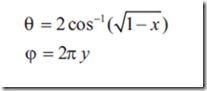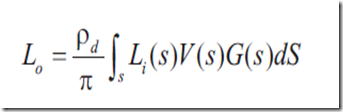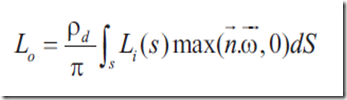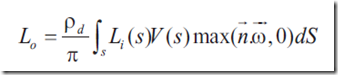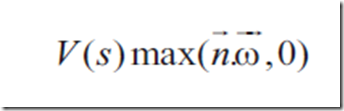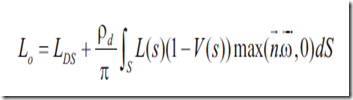【转自:http://www.cnblogs.com/daniagger/archive/2012/05/29/2524133.html】
1、背景知识
1.1 光照表示
之前我们都只考虑光源点和物体表面点的光照作用,而现在,我们考虑物体表面点延伸的微型平面,这个微型平面作为半球形的底部,因此光照射进来的范围就是整个半球形,这也是BRDF的基础。
1.2 数据压缩
对于压缩信号来说,很多压缩技术基于这样一个思路:使用不同基函数的不同组合来组成一个更为复杂的数字信号表示。
保存数字信号的最繁琐方法是保存每一个数据点,然而一个复杂的信号可能有成千上万个点,所以需要找到方法来压缩。对于每一个基函数,我们用频率(frequency),振幅(amplitude)和相位(phase)来表示,这三个数被称为系数(coefficient),这样就大大减小了数据量。
在现实生活中,数字信号并不能很明显的表示成多个基函数的组合,很多例子中,系数的个数和原始数据点的个数相差无几,所以要找寻其他压缩方法。人们要寻找信号中那些信息是最为重要的,有些信息可能是噪声,这些信息需要被剔除出去。
基函数是这样一种函数,可以被裁剪和组合,来模拟任何一种数学函数。裁剪因子通常被称为系数(coefficient)。举个例子,如果要通过基函数组Bi(x)来模拟函数f(x),ci是对应的系数。
公式如下图:
这也就是傅里叶变换。
1.3 光照信息的压缩
对于diffuse lighting来说,高频率的部分需要被剔除。
2、SH的定义
Spherical harmonics是可以重构任何函数的基函数,研究二维函数的单位球。
SH是定义在单位球表面的基函数,表示在球面坐标下。
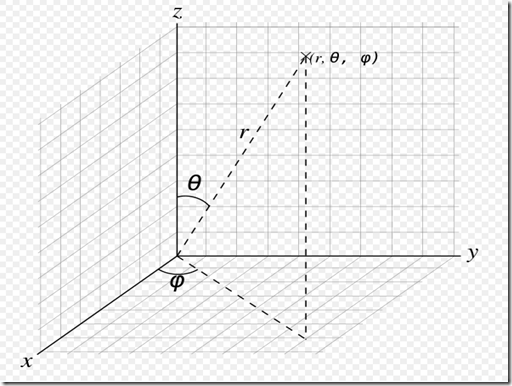
球坐标系
其中r=1。
SH的一般形式是
实际形式,也就是接下来会用到的形式是
最终形式是
公式中的项:
Plm是勒让德多项式,定义在[-1,1]范围内,递归式是
Klm是用来将函数规范化的裁剪因子,定义式是
SH的简化形式为(二维变一维)
3、构造
由SH基函数模拟的函数是
其中
上面的函数是原始函数的限制带宽版,原始函数表示为
使用SH的简化形式,则模拟的函数为
使用Monte Carlo积分算法,可以求出系数为
对于用SH构造的函数,你需要将单位球划分为n x n个样品,对于每一个系数,遍历所有的样品,应用上面的公式。最终可以得到所有系数的表达式。
4、SH的性质
4.1 正交性
4.2
4.3
5、SH应用到光照上
5.1 光照方程
最常用的光照方程是
Lo是表面顶点x在w方向上发出的光照度,其中w'是入射光线,由自发光部分(Le)和反射部分(Lr)组成,Lr的积分是对半球范围内所有的光线进行积分。
通过使用differential solid angle,光照方程可表示为
反射分量是对S中所有点的积分,入射光线从x’到x,V是x和x’之间可见度方程,G是几何项。V返回布尔值(如果x和x’相互可见,则返回1),几何项则依赖于表面点x和x’之间的几何关系。
该积分不能实时计算出来,所以需要预处理这个积分,利用性质2。
预处理步骤:
a、将入射光线投影到SH基上。入射光线需要表示成球坐标方程。
b、对于物体上的每一个点,将BRDF项、可见项、几何项的乘积投影到SH基上。该乘积也被当做转移方程。
实时积分项可以通过计算转移方程的SH系数和入射光线的SH系数的点积而得到,即利用性质2,将入射光线当成复合函数,BRDF项可见项几何项的乘积当做另一个复合函数,原始积分也就是两个复合函数乘积的积分。
同时,取样点分布在n x n的方形网格上,投影到球坐标系
现在我们需要简化光照方程,我们不考虑自发光,并且反射光线均匀分布在所有方向,BRDF是一个常量,最终我们得到
6、SH Diffuse Lighting
不考虑阴影的情况下(V项恒为1),特定点的diffuse lighting为
现在需要求入射光线的SH投影和cosine项(即转移方程)的SH投影,两者都用Monte Carlo积分法,这些都在预处理步完成。运行时,特定点的光照计算使用上述公式(将两个SH系数求点积)。
7、SH Diffuse Shadowed Lighting
现在需要考虑V项
新的转移方程变成了
要确定V项,需要从当前顶点追踪射线到场景中,如果射线和一个三角面片相交,则光线被阻挡。
8、SH Diffuse Shadowed Inter-Reflected Lighting
现在,不仅要考虑从光源发出来的光线,还要考虑在场景中互相作用的光线。也就是全局光照。简化了的光照方程如下