Github地址
https://github.com/Donemeb/SudukuProject
ps:名字好像起错了> <
PSP2.1 估计&实际
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) | |
| Planning | 计划 | 10 | 12 | |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 12 | |
| Development | 开发 | 1610 | 2350 | |
| · Analysis | · 需求分析 (包括学习新技术) | 40 | 30 | |
| · Design Spec | · 生成设计文档 | 20 | 25 | |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 5 | |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 20 | 10 | |
| · Design | · 具体设计 | 20 | 60 | |
| · Coding | · 具体编码 | 1440 | 2100 | |
| · Code Review | · 代码复审 | 30 | 60 | |
| · Test | · 测试(自我测试,修改代码,提交修改) | 30 | 120 | |
| Reporting | 报告 | 95 | 115 | |
| · Test Report | · 测试报告 | 30 | 50 | |
| · Size Measurement | · 计算工作量 | 5 | 5 | |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 60 | 60 | |
| 合计 | 1715 | 2477 |
有很大一部分时间花在调bug上了(捂脸)。一开始没有仔细记录好各个参数的具体含义和范围,过一段时间修改时凭记忆去改那些参数,超容易产生各种小bug。
需求分析
- 命令行形式
- 9*9 数独生成,首位为特定数字
- 9-9 数独求解
设计思路
先说说等价数独。一个数独终局通过各类变换可以生成超大量的等价数独。但是,由于题目中提到了不重复原则,假使要求生成的数独数量大于一个等价数独组,那么查重部分就会消耗大量的时间,反而得不偿失。也没有找到一个能识别不同等价数独的特征。便放弃了这个想法。
不考虑等价数独,数独的生成和求解,在本质上都可归为求解数独的过程,只不过生成相对于全0的数独求解,且不会因得出一个解答停止。
第一个想到的方法,大约也是最简单粗暴的方法,就是无脑递归遍历,输出可行解。通过每次检查插入是否可行来决定往下一层or继续尝试,但同时想到,检查插入的可行性本身是一个极占运行比重的部分,即使可以一次计算出一个递归过程中的所有可填入值,单纯通过数独局来遍历仍会占去大量运行时间。于是开始考虑如何存储每次递归过程冲突信息,以快速检查插入的可行性。
由于也是一个回溯算法,加之判断冲突,便联想到了N皇后问题。在查找资料的过程中,这篇博客给了我很大启发。通过划分冲突种类,以0|1方式表示冲突与否,很大程度上减少了建立、回溯冲突表本身,以及冲突表使用所花费的时间。同时这个方法特别适合在一次填完一个数字的回溯方法中使用。这也就是我之后程序的基本思路。
最终的设计思路:一次填完一个数字,每个数字按第一行往第九行的顺序填入,冲突表有三个:列冲突表[每个数字],九宫格冲突表[每个数字],整体的数独冲突表
具体实现
建立一个suduku类,提供生成、解数独方法。
- sudu_generation 生成的入口方法
- sudu_gene_init 初始化开局(决定回溯顺序、确定首位为5)
- sudu_gene_loop 递归函数
- sudu_insert_0 冲突表插入
- sudu_delete_0 冲突表回退
- sudu_solve 解答的入口方法
- sudu_solve_new
- sudu_solve_init初始化开局
- sudu_solve_loop 递归函数
- sudu_insert_0 冲突表插入
- sudu_delete_0 冲突表回退
- sudu_to_file 数独写入文件
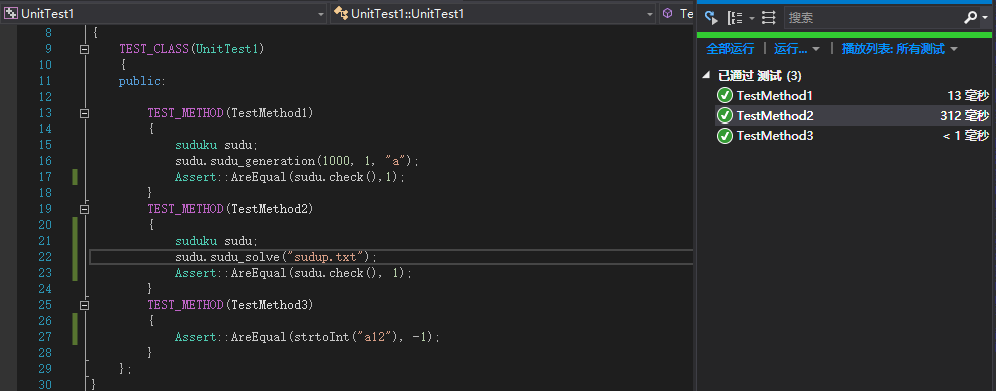
单元测试
有很多是private方法,难以从外部调用。测试函数采用调用入口函数,检查数独终局的正确性的方式来进行测试。另有命令行输入的数字的合法性的检测。
代码优化
生成部分的代码写完后,迫不及待的试了一试——1s、10s、100s...当我终于忍不下去了强制结束程序时,不过输出了20w个数独。问题很快就发现了:文件IO。当时采用的是一个数字一个数字输出到文件的方式,极其拖慢性能。之后我为其申请了一个输出到文件的buf,每次调用sudu_to_file时先将输出暂存在buf中,等buf快满了,一次性输出到文件。在程序结束前再调一次sudu_to_file_flush来将还在buf中的数据输出到文件。
接下来做了一些小优化。删去了代码中的一些多余的计算等。
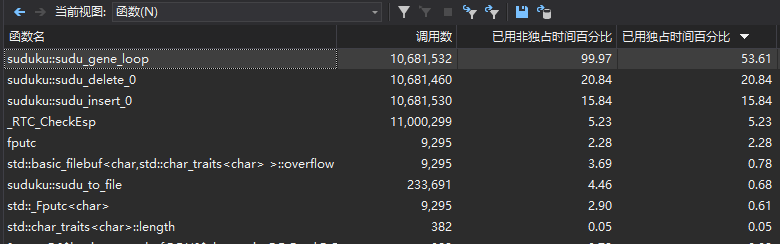
- 代码性能图
数独生成
数独求解
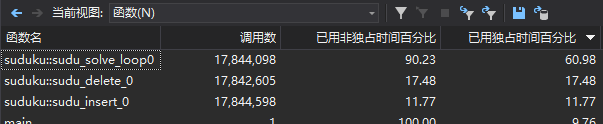
可以发现函数消耗的比例很相似,因为解答时基本使用的是同一个算法。
-
100w生成测试
在我的电脑上,release版本,生成100w数独的时间在6s上下。 -
消耗最大的函数
即回溯过程
void sudu_gene_loop(int order, int & now_num, int target_num) {
int canset = 0;
int depth = order % 9;
int order_num = order / 9;
int num = rand_num_order[order_num];//ATTENTION 是否可以直接除
int i;
if (order == 0) {
sudu[0] = num + 1;
gene_row[num] = gene_row[num] | 0400;
gene_hasput[depth] = gene_hasput[depth] | 0400;
gene_33[0] = 0700;
sudu_gene_loop(order + 1, now_num, target_num);
}
else {
if (now_num == target_num) return;
canset = gene_row[num] | gene_hasput[depth] | gene_33[order_num * 9 + depth / 3];
for (int i1 = 1; i1 < 10; i1++) {
i = rand_posi_order[order * 9 + i1 - 1]; //change the name of i
if (!(canset & x1[i])) {
//放入数据表
if (order == 80) {
sudu[depth * 9 + i] = num + 1;
sudu_to_file();
sudu[depth * 9 + i] = 0;
now_num++;
return;
// sudu_out << now_num;
//输出到文件 //ATTENTION 考虑缓存、效率
}
//更新冲突表
sudu_insert_0(i, num, depth, order_num);
sudu_gene_loop(order + 1, now_num, target_num);
if (now_num == target_num) return;
sudu_delete_0(i, num, depth, order_num);
}
}
}
}
- 代码覆盖率

代码说明
回溯中判断可行操作的关键代码(即冲突表的使用):
canset = gene_row[num] | gene_hasput[depth] | gene_33[order_num * 9 + depth / 3];
for (int i1 = 1; i1 < 10; i1++) {
i = rand_posi_order[order * 9 + i1 - 1]; //change the name of i
if (!(canset & x1[i])) {
//放入数据表
…………
冲突表的插入:
num是当前插入的数字(0-8),i是列数,depth是行数,order_num是总回溯中的顺序(0-80)
ps:由于在一开始随机了各种顺序参数(下面的其他会说到,所以记录了回溯顺序)
void sudu_insert_0(int i, int num, int depth, int order_num) {
sudu[depth * 9 + i] = num + 1;
gene_row[num] = gene_row[num] | x1[i];
gene_hasput[depth] = gene_hasput[depth] | x1[i];
if (depth < 3) {
if (i <= 2) {
gene_33[order_num * 9 + 0] |= 0700;
}
else if (i <= 5) {
gene_33[order_num * 9 + 0] |= 0070;
}
else if (i <= 8) {
gene_33[order_num * 9 + 0] |= 0007;
}
}
else if (depth < 6) {
if (i <= 2) {
gene_33[order_num * 9 + 1] |= 0700;
}
else if (i <= 5) {
gene_33[order_num * 9 + 1] |= 0070;
}
else if (i <= 8) {
gene_33[order_num * 9 + 1] |= 0007;
}
}
else if (depth < 8) {
if (i <= 2) {
gene_33[order_num * 9 + 2] |= 0700;
}
else if (i <= 5) {
gene_33[order_num * 9 + 2] |= 0070;
}
else if (i <= 8) {
gene_33[order_num * 9 + 2] |= 0007;
}
}
}
冲突表的回退:
插入的逆过程
void sudu_delete_0(int i, int num, int depth, int order_num) {
//ATTENTION 是否考虑回退模式?栈存储? 而不是再计算一遍
sudu[depth * 9 + i] = 0;//放入数据表
//更新冲突表
gene_row[num] = gene_row[num] & (~x1[i]);
gene_hasput[depth] = gene_hasput[depth] & (~x1[i]);
if (depth < 3) {
if (i <= 2) {
gene_33[order_num * 9 + 0] &= 0077;
}
else if (i <= 5) {
gene_33[order_num * 9 + 0] &= 0707;
}
else if (i <= 8) {
gene_33[order_num * 9 + 0] &= 0770;
}
}
else if (depth < 6) {
if (i <= 2) {
gene_33[order_num * 9 + 1] &= 0077;
}
else if (i <= 5) {
gene_33[order_num * 9 + 1] &= 0707;
}
else if (i <= 8) {
gene_33[order_num * 9 + 1] &= 0770;
}
}
else if (depth < 9) {
if (i <= 2) {
gene_33[order_num * 9 + 2] &= 0077;
}
else if (i <= 5) {
gene_33[order_num * 9 + 2] &= 0707;
}
else if (i <= 8) {
gene_33[order_num * 9 + 2] &= 0770;
}
}
sudu[depth * 9 + i] = 0;
}
数独、冲突表的初始化:
void sudu_solve_init() {
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (sudu[i * 9 + j] != 0) {
sudu_insert_0(j, sudu[i * 9 + j] - 1, i, sudu[i * 9 + j] - 1);
}
}
}
}
其他
- 一个无聊的功能。因为之前以为要生成随机数独,所以给写了些rand函数随机了一下回溯顺序。后来发现没必要,它也只是在开始时运行一次,并不耗什么时间,也就一直留了下来。所以每次生成数独时得到的数独基本是不一样的(同次的数独仍是由一个回溯顺序生成)
- 一开始时求解数独时使用了最简单的回溯法,后来改成类似生成的算法后,在测试中却发现仍是最开始的方法性能较优。暂时未找到原因。