treeMap

1.二叉树：树中的任何节点的值大于它的左子节点，且小于它的右子节点。

2.平衡二叉树：一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

3.红黑树：节点是红色或者黑色的平衡二叉树，它通过颜色的约束来维持着二叉树的平衡。

规则：每个节点都只能是红色或者黑色；根节点是黑色；每个叶节点（NIL节点，空节点）是黑色的；如果一个结点是红的，则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点；从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

4.treeMap是红黑树算法的实现。

5,。红黑树增加节点：插入新节点总是红色节点 ；如果插入节点的父节点是黑色, 能维持性质 ；如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质 。

6.插入节点：

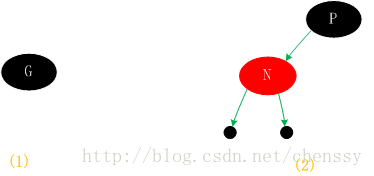
一.为根节点：若新插入的节点N没有父节点，则直接当做根据节点插入即可，同时将颜色设置为黑色。（如图一（1））

二.父节点为黑色:这种情况新节点N同样是直接插入，同时颜色为红色，由于根据规则四它会存在两个黑色的叶子节点，值为null。同时由于新增节点N为红色，所以通过它的子节点的路径依然会保存着相同的黑色节点数，同样满足规则5。（如图一（2））

三.若父节点P和P的兄弟节点U都为红色： 对于这种情况若直接插入肯定会出现不平衡现象。怎么处理？P、U节点变黑、G节点变红。这时由于经过节点P、U的路径都必须经过G所以在这些路径上面的黑节点数目还是相同的。但是经过上面的处理，可能G节点的父节点也是红色，这个时候我们需要将G节点当做新增节点递归处理。

四.若父节点P为红色，叔父节点U为黑色或者缺少，且新增节点N为P节点的右孩子： 对于这种情况我们对新增节点N、P进行一次左旋转。这里所产生的结果其实并没有完成，还不是平衡的（违反了规则四），这是我们需要进行情况5的操作。

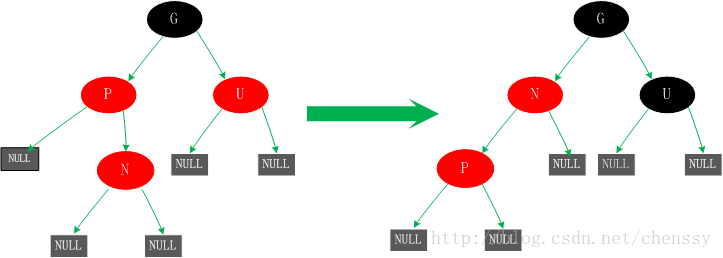
五.父节点P为红色，叔父节点U为黑色或者缺少，新增节点N为父节点P左孩子: 这种情况有可能是由于情况四而产生的，也有可能不是。对于这种情况先已P节点为中心进行右旋转，在旋转后产生的树中，节点P是节点N、G的父节点。但是这棵树并不规范，它违反了规则4，所以我们将P、G节点的颜色进行交换，使之其满足规范。开始时所有的路径都需要经过G其他们的黑色节点数一样，但是现在所有的路径改为经过P，且P为整棵树的唯一黑色节点，所以调整后的树同样满足规范5。

TreeMap put()方法实现分析：第一：构建排序二叉树，第二：平衡二叉树。

 对于排序二叉树的创建，其添加节点的过程如下：

•        1、以根节点为初始节点进行检索。

•        2、与当前节点进行比对，若新增节点值较大，则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。

•        3、循环递归2步骤知道检索出合适的叶子节点为止。

•        4、将新增节点与3步骤中找到的节点进行比对，如果新增节点较大，则添加为右子节点；否则添加为左子节点。

参考文献：http://blog.csdn.net/chenssy/article/details/26668941