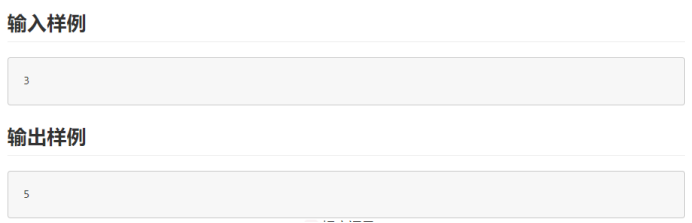
题目描述:
样例:
实现解释:
一道看似复杂但实际既是斐波那契变形的题目
知识点:递推,斐波那契
通过问题的描述,可以得到以下规律:(除了座位数为一时)男生坐最后时,倒数第二个一定是女生;女生坐最后,倒数第二个均可。转化:i个位置时男生结尾的情况数等于i-1个位置时女生结尾的情况数,i个位置时女生结尾的情况数等于i-1个位置时的总情况数。
于是便可得出两种解决方案:斐波那契变形和直接循环递推
斐波那契变形:
i位置男生结尾的情况 = i-1位置女生结尾情况数 = i-2位置总情况数
i位置女生结尾的情况 = i-1位置总情况数
则有num(i) = num(i-1)+num(i-2); num(1) = 2; num(0) = 1;
编写递归程序即可。
直接循环递推:
直接按转化后的递推关系编写程序即可:利用temp储存前一次男生结尾情况,男生结尾数 = 前一次的女生结尾数,女生结尾数 = 前一次女生结尾数加上存储好的前一次男生结尾数即可。
最后的代码还包括一个没事儿干的时候进行代码缩减后的递推代码,省去了temp变量。
坑点:
斐波那契方法时注意特殊值0和1的判断输出
递推方法时注意两种选择情况的重置
完整代码:
斐波那契变形:
//斐波那契变形 直接斐波那契
#include<iostream>
using namespace std;
int fi(int n)
{
if(n == 0) return 1;
if(n == 1) return 2;
return fi(n-1)+fi(n-2);
}
int main()
{
ios::sync_with_stdio(false);
int n;
while(cin >> n)
{
cout << fi(n) << '\n';
}
return 0;
}
直接循环递推:
#include<iostream>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
int n;
long long temp,choiceMan,choiceWoman;
//分别为中间值,男生坐最后的情况总数,女生坐最后的情况总数
while(cin >> n)
{
//一个座位时,男女最后的情况分别为1
choiceMan = choiceWoman = 1;
for(int i = 1;i<n;i++)
{
//记录
temp = choiceMan;
//座位增多后,男生只能坐在女生结尾的座位后
choiceMan = choiceWoman;
//女生可以女生最后也可以男生最后,求和
choiceWoman += temp;
//注意交换赋值的顺序
}
cout << choiceMan+choiceWoman << endl;
}
return 0;
}
无聊压缩代码:
#include<cstdio>
int main()
{
int n,m,w;
while(~scanf("%d",&n))
{
m=w=1;
while(n-->1)
{
w+=m;
m=w-m;
}
printf("%d\n",m+w);
}
}