感觉十分厉害的题,记录一下(
有个很显然的 (mathcal{O}(nmax a)) 的 dp,设 (f_{i,j}) 为 (a_i) 变为 (j),考虑原序列 ([1,i]) 的最小代价。
显然有:
结论1:(f_{i,j}) 关于 (j) 的点相邻两个连起来是一个下凸壳。
证明:
(f_{1,j}=|a_1-j|),是一个绝对值函数,顶点在 (a_1)。
考虑 (f_{i-1} o f_{i}) 会发生怎样的变化。
分类讨论一下,具体可以看这里的证明,我认为写得非常地好,无需多补充,不过请务必看懂有关下凸壳的证明,后面的做法会涉及到加入 (a_i) 对下凸壳线段的影响。
下凸壳的斜率肯定是递增的。先钦定线段的斜率是不断 (+1) 的,如果中间出现了断层的现象就当作这个断的地方有长度为 (0) 的线段,这些线段的斜率补充了中间断层的地方。
再设 (op_i) 为 (f_i) 的斜率为 (0) 的那一条线段的左端点,也是斜率为 (1) 的那一条线段的右端点。
我们需要明确一点,最终答案是 (f_{n,op_n}),换句话说,我们只关心 (f_{n,op_n}) 的纵坐标,不关心 (op_n) 具体是几,因为问题只要求输出最小的代价。
现在可以完全不管斜率 (>1) 的线段了,它们怎么变和求答案没有关系。
考虑维护这些斜率 (leq 0) 的线段,设计一个可重元素的由大到小的优先队列(或者说大根堆),其元素为线段的右端点,一个右端点可以重复多次,其线段的斜率为其需要完全 pop 出的次数的相反数。
举个栗子,大根堆为 ({3,2,2,1,1}),那么右端点为 (2) 的线段的斜率为 (-3),因为弹出全部的 (2) 需要把一个 (3),两个 (2) 全部弹出。
现在惊奇地发现,这个优先队列恰好对上了我们前面钦定的斜率不断 (+1) 递增"的"暴论"。
关于要用到的结论上面给出的链接已经证明,我现在重新叙述一遍。
-
线段单降且在 (a_i) 左侧,斜率 (-1)(其斜率的数值减去 (1));
-
线段单降且在 (a_i) 右侧,斜率 (+1);
-
线段不单降且在 (a_i) 左侧,斜率变为 (-1);
-
线段不单降且在 (a_i) 右侧,斜率变为 (1);
考虑从 (f_{i-1}) 到 (f_i),一个 (a_i) 会对答案造成怎样的影响。
设答案为 (ans),也就是考虑 (i) 增加时 (ans) 如何改变。
Case1: (a_igeq op_{i-1})
这个时候 (a_i) 前面的线段斜率都 (<0) 了,而 (op_{i-1}) 又是 (f_{i-1,j}) 取到最小值时的 (j),又在 (a_i) 前面,所以可以从 (op_{i-1}) 转移而来。答案变为 (f_{i,a_i}) 处的取值即为 (f_{i-1,op_{i-1}}+|a_i-a_i|),(ans) 不变。
由于前面的线段斜率都会 (-1),要维护堆的意义,就把 (a_i) push 进堆中,这样堆中所有元素其 pop 完的次数都 (+1),则斜率就 (-1)。

Case2: (a_i<op_{i-1})
首先考虑答案改变成什么样子,注意到新的决策点 (op_i) 即为图中红点和 (op_{i-1}) 之间的斜率变为了 (0),所以 (f_{i,op_i}=f_{i,op_{i-1}}=f_{i-1,op_{i-1}}+op_{i-1}-a_i)。例如图中,这个时候每部分的线段的斜率由图中黑色的变成红色的,中间有一段 (-3,-1) 中间断开了,少了 (-2),换句话说,由于我们 push 进去了 (a_i),还想要维护堆的意义,就要把 (op_{i-1}) 弹出,再把 (a_i) 压进去,使其拥有斜率为 (-2) 的段。
我们要维护堆能够以 (1) 递增实际上是让每次 (a_i<top) 的时候保证加进去 (a_i) 后 (top) 作为右端点代表的线段斜率变为了 (-1),保证它一定是需要弹出的点。所以多 push 进去是对的。
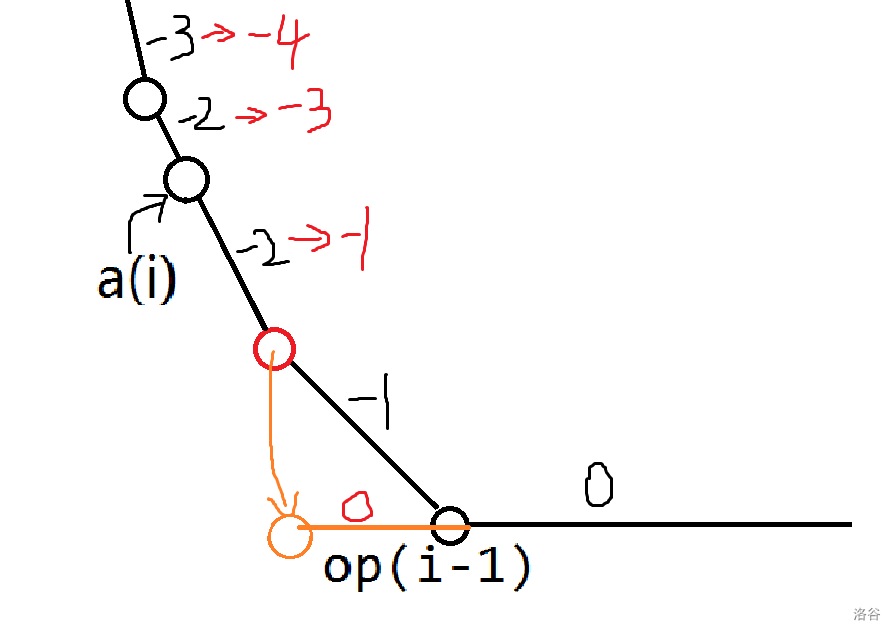
图中为一个栗子,值得注意的是两条线段之间的长度可能为 (0),但这不影响答案。
综上所述,我们得到了一个很简洁的代码来完成这个过程。
时间复杂度 (mathcal{O}(nlog n))
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
template <typename T> T Max(T x, T y) { return x > y ? x : y; }
template <typename T> T Min(T x, T y) { return x < y ? x : y; }
template <typename T>
T &read(T &r) {
r = 0; bool w = 0; char ch = getchar();
while(ch < '0' || ch > '9') w = ch == '-' ? 1 : 0, ch = getchar();
while(ch >= '0' && ch <= '9') r = (r << 3) + (r << 1) + (ch ^ 48), ch = getchar();
return r = w ? -r : r;
}
const int N = 500010;
int n, a;
std::priority_queue<int>q;
long long ans;
signed main() {
read(n);
for(int i = 1; i <= n; ++i) {
read(a); q.push(a);
if(a < q.top()) {
ans += q.top() - a;
q.pop();
q.push(a);
}
}
printf("%lld
", ans);
return 0;
}
感谢slyz的两位学长的指点以及 Mr_Wu 的题解。
笔者才疏学浅,如有错误欢迎指出,如有疑惑也欢迎提出。