本文提出了使用异构点线特征的slam系统,继承了ORB-SLAM,包括双目匹配、帧追踪、局部地图、回环检测以及基于点线的BA。使用最少的参数对线特征采用标准正交表示,推导了线特征重投影误差的雅克比矩阵,改进了实验结果。因为使用线特征能够提供更多的几何约束,传统的方法只使用了点特征,对光照变化以及位置歧义较为敏感。但是线特征也有两个问题要解决:首先是空间中的线参数太多,图优化时计算量增加,空间中的线只有四个自由度,但是通常被表示成6个自由度(端点表示以及Plucker坐标);其次,由于参数过多,大多数线特征法都采用数值计算雅克比,而本文中推导了了雅克比矩阵,提高精确度。
总之,本文统一了代价函数,将点线重投影误差结合,前端提出改进方法提取并匹配线特征,后端线特征采用标准正交表示,参数最少且解耦合,为了最小化重投影误差,推导了雅克比矩阵。
线特征的检测和表示
A.提取描述线特征
作者改进了使用较多的LSD线段特征检测器,该方法虽然在噪声较大的各种环境都能运行,但是容易将一条线段分为好几段。为了改进这一点,作者通过比较前一条线的最后一个点和下一条线的第一个点距离,以及两条线段中点之间的距离,如果都比给定的阈值小,且线段方向差异较小。(上面提到的距离都是描述子之间的距离,点特征为ORB特征,线特征为LBD特征(文献[14]) )。
B.线段特征匹配
匹配的线段几何特征要求参考文献[15],本文两条线匹配要满足以下要求:
1)两条线之间的角度不超过一个阈值
2)两条线的长度差不多
3)两条线重合的长度超过一个阈值(这里的重合应该是在两张图片相同区域???)
4)两条线的LBD描述子距离小于阈值
C. 几何表示
三维空间的直线,可以用两个齐次或者非齐次坐标表示,齐次坐标与Plucker坐标之间的转换见公式(1),用一个6维的向量表示:方向向量+法向量。由于三维直线只有四个自由度,而上面的表示为6个自由度,后端优化增加了计算量,因此参考了文献[11]中的标准正交表示。最终只要四个参数的(delta _ heta)表示,具体对直线的几何表示见图(5)。
对点线测量进行图优化
A.点线特征测量模型
(T_{cw})表示世界和相机之间的转换矩阵,直线从世界坐标转换到相机坐标系下见公式(7),参考了文献[16],这里是Plucker坐标,因此与笛卡尔坐标系的公式不一样,再通过内参投影到图像上,见公式(8)。重投影误差即为匹配线段与重投影到图像上的线段之间的端点距离。
相机位姿、3D点位置、3D线位置为图优化中的顶点(即优化变量)。而边则为点和线的重投影误差,见公式(10)和(11)。假设观测遵循高斯分布,使用huber核构建代价函数,见公式(12)。
B.线重投影误差的雅克比
这里推导对位姿变化的雅克比以及四自由度的(delta _ heta)雅克比,使用链式法则求导,误差函数对投影的线(l')的导数见公式(13),投影线对Plucker坐标的导数见公式(14)。Plucker坐标在相机系下的表示对在世界坐标系下的表示见公式(15),后者对(delta _ heta)的导数见公式(16),因此(delta _ heta)的雅克比即可求出来。而Plucker坐标在世界坐标系下的表示对位姿的变化求导较为困难(为什么困难?)。将其分为两个部分求解,平移微小变化和旋转微小变化,对平移增量求导时旋转增量设为0,对旋转矩阵加一个微小量,得到Plucker坐标在世界坐标系下新的表达,则可以得到其对平移量的导数,对旋转量的导数见公式(22),证明见附录。
求出雅克比之后即可使用高斯牛顿法求解图优化问题。
实验:
基于ORB-SLAM2,三个并行线程:追踪、局部地图、回环检测。
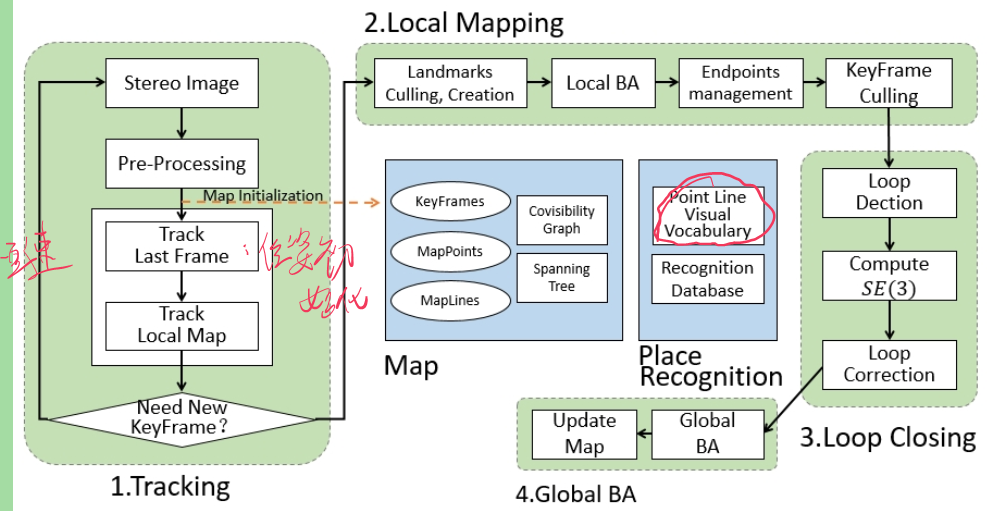
不同之处:
1)追踪
校正过的双目图像作为输入,四个并行线程用于提取左右相机中的特征点(ORB特征)。LSD检测线特征,使用LBD描述子。随后两个线程用于双目匹配,所有的特征都被区分为双目或者单目特征,如图所示
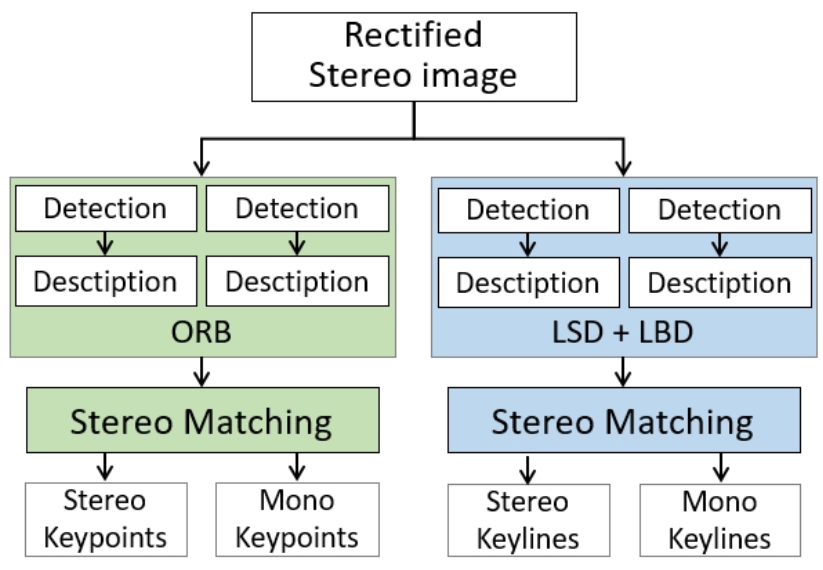
对于单目特征,在其他关键帧中找一个未匹配的特征,一旦找到匹配的特征,进行三角化。
运动估计分两种类型:追踪上一帧以及追踪局部地图。追踪上一帧时,使用恒速模型预测相机位姿作为先验,当位姿先验已知,则地图点和线可以投影到当前帧,建立更多联系。3D线投影时与点投影不一样,可能只有部分被观测到,如图所示,
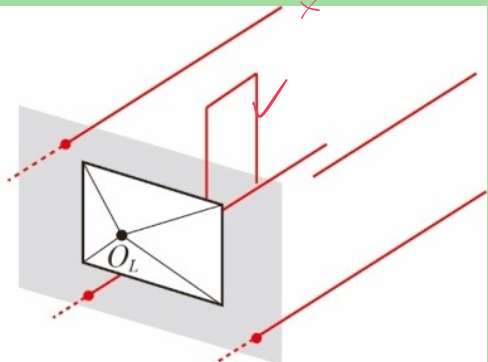
虚线不能被观测到而实线可以观测。为了保证投影的2D线被观测到,使用基于剔除的方法:
-
将3D线从世界坐标投影到当前坐标,计算两个端点(X_{sk})以及(X_{ek})。
-
如果两个点都在相机后面,丢弃该线。如果一个点在相机后面,计算相机面与3D直线之间的交点。
-
将3D点投影到相机平面前方,投影线可能超出相机平面边界,使用Liang-Barsky 进行线修剪,可以保持旋转不变性。
关键帧的选取在ORB-SLAM2的基础上添加了线特征的要求。
2)局部地图:新的关键帧增加是,当前帧和其他帧的共视信息将被更新,局部地图三角化更多的点和线。移除外点,删除冗余帧。相机位姿和路标使用BA进行优化。由于3D线的端点对优化没有影响,但是对匹配和可视化很有用,因此在优化后系统仍然维护3D线的端点。通过反投影2D线到当前帧,并进行修剪。(与SLSLAM类似)
3)回环检测以及全局BA
视觉词袋预先离线训练,用到点特征和线特征,使用ORB特征和LBD特征建立词典,两个单词向量的相似度度量见公式(26)。使用时间一致性完善了匹配的关系,回环时使用SE(3)变换(采用Ransac策略)计算出变换矩阵,如果失败,则使用文献[23]中的方法,采用双目视觉中的匹配直线,最后计算的位姿用于纠正回环。再计算全局BA。
A
面特征行不行?
观测为什么服从高斯分布?
公式(9)怎么理解