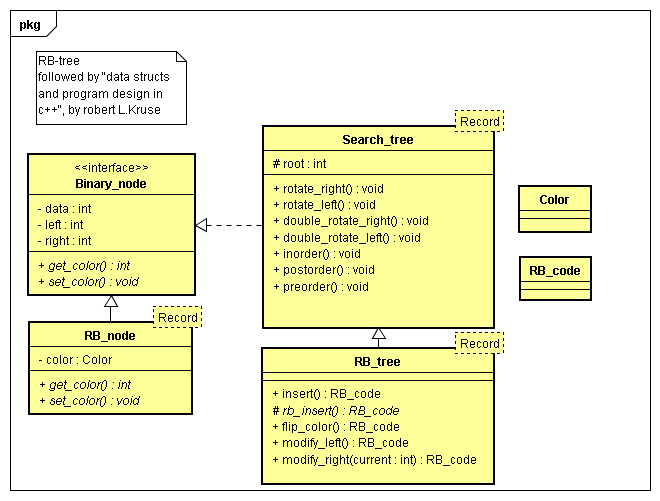
1、二分查找与二叉树:效率、空间、灵活性的权衡
数据与链表的互补:
数组: 查找快(使用二分叉找)->log2N 。插入和删除极为不便。->移动其它数据的开销。要保持数据有序,则必然有大量的插入删除操作。
链表: 为每个元素带上两个指针,分别指向其前结点和后结点。
1)打破了数据对空间相关性的依赖。避免了插入删除时移动数据的开销。
2)不能使用二分查找。
为了能在链表中使用二分叉找,我们将元素的指针做一些改变:不再指向其前后元素。而指向其二分结点元素。
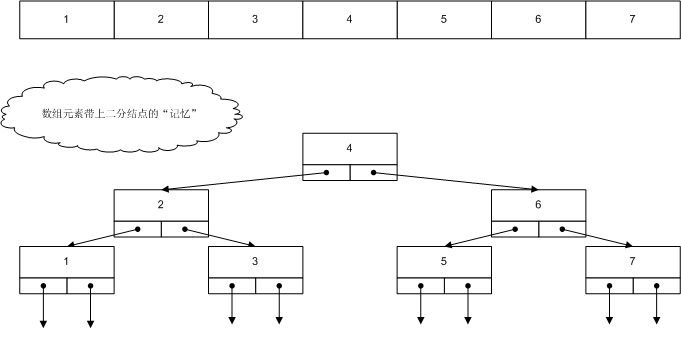
其数据结构定义如下:
template <class Entry>
struct Binary_node
{
Entry data;
Binary_node<Entry> *left;
Binary_node<Entry> *right;
}
插入和删除引起了二叉树的不平衡。struct Binary_node
{
Entry data;
Binary_node<Entry> *left;
Binary_node<Entry> *right;
}
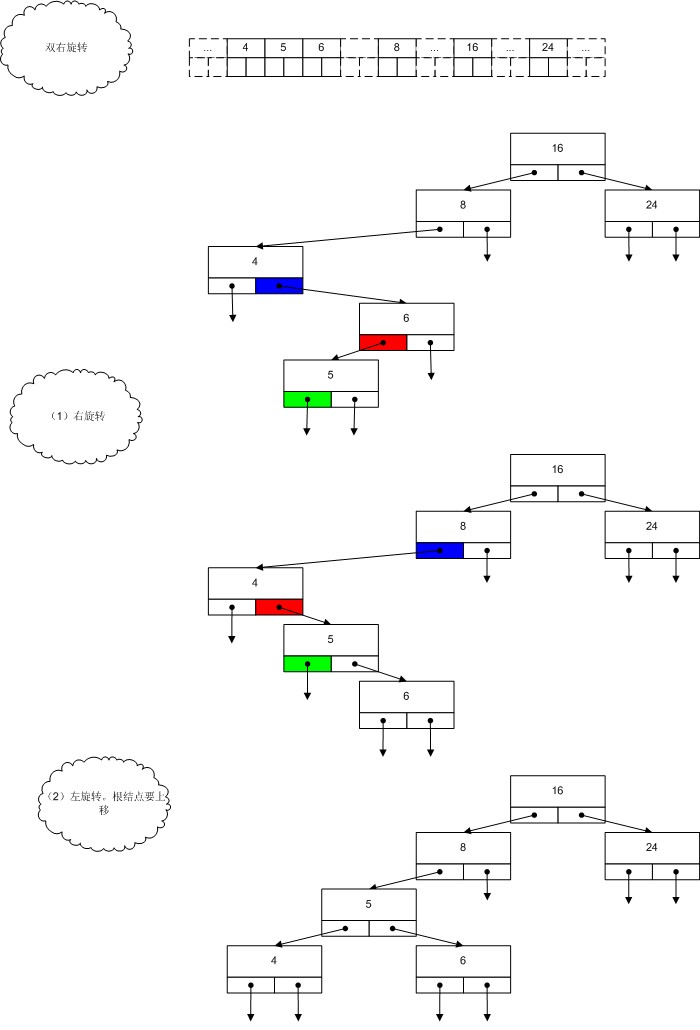
我们将数组的范围扩大到 1-24,而且经过删除操作,只剩下了如下图的7个元素:
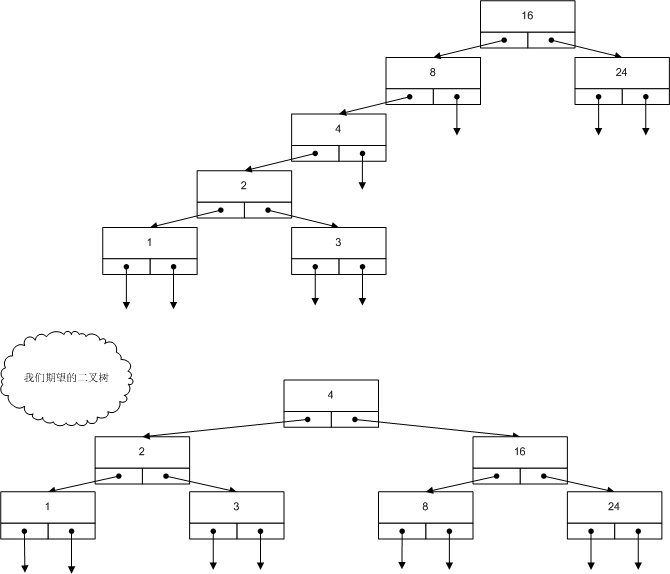
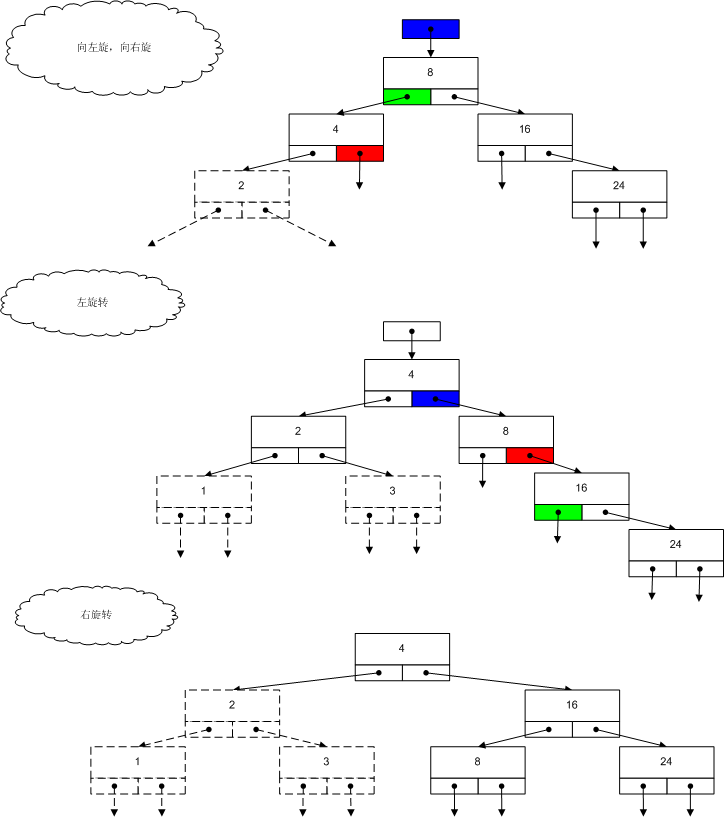
任何的不平衡,可以通过两种旋转操作来完成:左旋转、右旋转。
调整三个结点的关系: 孙子结点、父结点、爷爷结点。
修改三个指针值:指向爷爷结点的指针(当前根结点)、指向父结点的指针、指向叔父结点的指针。
template <class Record>
Error_code Search_tree<Record> :: rotate_right( Binary_node<Record> * ¤t )
{
Binary_node<Record>* reg = current->left;
current->left = reg->right;
reg->right = current;
// 正确地指向当前根结点
current = reg;
return okay;
}
template <class Record>
RB_code Search_tree<Record> :: rotate_left(Binary_node<Record> * ¤t )
{
Binary_node<Record>* reg = current->right;
current->right = reg->left;
reg->left = current;
// 正确地指向当前根结点
current = reg;
return okay;
}
Error_code Search_tree<Record> :: rotate_right( Binary_node<Record> * ¤t )
{
Binary_node<Record>* reg = current->left;
current->left = reg->right;
reg->right = current;
// 正确地指向当前根结点
current = reg;
return okay;
}
template <class Record>
RB_code Search_tree<Record> :: rotate_left(Binary_node<Record> * ¤t )
{
Binary_node<Record>* reg = current->right;
current->right = reg->left;
reg->left = current;
// 正确地指向当前根结点
current = reg;
return okay;
}
Error_code Search_tree<Record> ::double_rotate_left(Binary_node<Record> * ¤t )
{
rotate_right( current );
rotate_left( current );
return okay;
}
template <class Record>
Error_code Search_tree<Record> :: double_rotate_right(Binary_node<Record> * ¤t )
{
rotate_left( current );
rotate_right( current );
return okay;
}
{
rotate_right( current );
rotate_left( current );
return okay;
}
template <class Record>
Error_code Search_tree<Record> :: double_rotate_right(Binary_node<Record> * ¤t )
{
rotate_left( current );
rotate_right( current );
return okay;
}
红黑树--懒汉平衡
红黑树 vs 平衡二叉树
1)性能几乎没有下降
2)减少了开销
基本思想:从根结点开始,层与层红黑相间。直有两层黑的相遇,才旋转。
红黑树的基本操作:
1)着色:flip_color()
2) 旋转:借用 search-tree 的方法。
红黑树结点的四种状态:
enum RB_code { okay, red_node, left_red, right_red };
okey: 合法的红黑树。red_node: 树结构平衡,根结点颜色为红。
left_red: 树结构不平衡,左子结点为红。
right_red:树结构不平衡,右子结点为红。
红黑树的叶子结点:概念上存在而物理上不存在。
最坏情况:
插入操作:
删除操作:
应用:
多数应用中,结点还包含一个父结点:
// Linux-2.6.17/include/linux/rbtree.h
struct rb_node
{
unsigned long rb_parent_color;
#define RB_RED 0
#define RB_BLACK 1
struct rb_node *rb_right;
struct rb_node *rb_left;
} __attribute__((aligned(sizeof(long))));
/* The alignment might seem pointless, but allegedly CRIS needs it */
// stl/stl_tree.h
struct _Rb_tree_node_base
{
typedef _Rb_tree_Color_type _Color_type;
typedef _Rb_tree_node_base* _Base_ptr;
_Color_type _M_color;
_Base_ptr _M_parent;
_Base_ptr _M_left;
_Base_ptr _M_right;
};
template <class _Value>
struct _Rb_tree_node : public _Rb_tree_node_base
{
typedef _Rb_tree_node<_Value>* _Link_type;
_Value _M_value_field;
};
struct rb_node
{
unsigned long rb_parent_color;
#define RB_RED 0
#define RB_BLACK 1
struct rb_node *rb_right;
struct rb_node *rb_left;
} __attribute__((aligned(sizeof(long))));
/* The alignment might seem pointless, but allegedly CRIS needs it */
// stl/stl_tree.h
struct _Rb_tree_node_base
{
typedef _Rb_tree_Color_type _Color_type;
typedef _Rb_tree_node_base* _Base_ptr;
_Color_type _M_color;
_Base_ptr _M_parent;
_Base_ptr _M_left;
_Base_ptr _M_right;
};
template <class _Value>
struct _Rb_tree_node : public _Rb_tree_node_base
{
typedef _Rb_tree_node<_Value>* _Link_type;
_Value _M_value_field;
};
fdfd