摘要: 本文由digging4发表于:http://www.cnblogs.com/digging4/p/5091536.html
统计建模与R软件-第七章 方差分析
7.1 三个工厂生产同一种零件,现从各厂产品中分别抽取4件产品作检测,其检测强度如表7.25所示。
表7.25 产品检测数据
| 工厂 |
零件强度 |
| 甲 |
115 116 98 83 |
| 乙 |
103 107 118 116 |
| 丙 |
73 89 85 97 |
(1)对数据作方差分析,判断三个厂的产品的零件强度是否有显著差异
(2)求每个工厂生产产品零件强度的均值,作出相应的区间估计((alpha=0.05))
(3)对数据作多重检验。
df <- data.frame(X = c(115, 116, 98, 83, 103, 107, 118, 116, 73, 89, 85, 97),
A = gl(3, 4))
fit.aov <- aov(X ~ A, data = df)
summary(fit.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 2 1304 652 4.92 0.036 *
## Residuals 9 1192 132
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 由于P值为0.036,小于0.05,因此认为因素A(三个厂)对零件强度有显著差异。
plot(df$X ~ df$A)
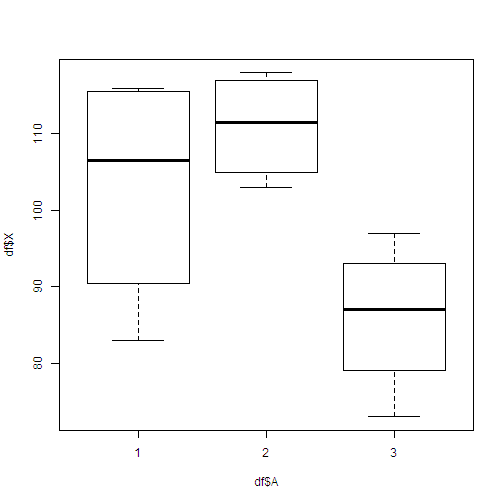
# 从箱线图也可以看出三个工厂的零件强度有显著差异。
# 对三个厂的零件强度求均值及其区间估计
mean.1 <- mean(df$X[df$A == 1])
mean.1.t <- t.test(df$X[df$A == 1], conf.level = 0.95)
mean.2 <- mean(df$X[df$A == 2])
mean.2.t <- t.test(df$X[df$A == 2], conf.level = 0.95)
mean.3 <- mean(df$X[df$A == 3])
mean.3.t <- t.test(df$X[df$A == 3], conf.level = 0.95)
reulst <- data.frame(A = c(1, 2, 3), mean = c(mean.1, mean.2, mean.3), t.test.down = c(mean.1.t[4]$conf.int[1],
mean.2.t[4]$conf.int[1], mean.3.t[4]$conf.int[1]), t.test.up = c(mean.1.t[4]$conf.int[2],
mean.2.t[4]$conf.int[2], mean.3.t[4]$conf.int[2]))
reulst
## A mean t.test.down t.test.up
## 1 1 103 78.04 128.0
## 2 2 111 99.60 122.4
## 3 3 86 70.09 101.9
# 对数据做多重检验
pairwise.t.test(df$X, df$A, p.adjust.method = "none")
##
## Pairwise comparisons using t tests with pooled SD
##
## data: df$X and df$A
##
## 1 2
## 2 0.351 -
## 3 0.066 0.013
##
## P value adjustment method: none
# 可以看到1和2的p值为0.351,可认为两水平无差异。
# 1和3的P值0.066有差异,不显著;2和3的P值0.013,差异显著。
# 结论为工厂丙的零件强度与其他两个厂有显著差异,甲乙两厂无差异。
7.2有四种产品,(A_i,i=1,2,3)分别为国内甲、乙、丙三个工厂生产的产品,(A_4)国外同类产品,现从各厂分别取10,6,6和2个产品做300小时连续磨损老化试验,得变化率如表7.26所示,假定各厂产品试验变化率服从等方差的正态分布。
表7.26 磨损老化试验数据
| 产品 |
变化率 |
| (A_1) |
20 18 19 17 15 16 13 18 22 17 |
| (A_2) |
26 19 26 28 23 25 |
| (A_3) |
24 25 18 22 27 24 |
| (A_4) |
12 14 |
(1)试问四个厂生产的产品的变化率是否有显著差异?
(2)若有差异,请做进一步的检验。i)国内产品与国外产品有无显著差异?ii)国内各厂家的产品有无显著差异?
df <- data.frame(X = c(20, 18, 19, 17, 15, 16, 13, 18, 22, 17, 26, 19, 26, 28,
23, 25, 24, 25, 18, 22, 27, 24, 12, 14), A = factor(rep(1:4, c(10, 6, 6,
2))))
fit.aov <- aov(X ~ A, data = df)
summary(fit.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 3 346 115.3 14.7 2.8e-05 ***
## Residuals 20 157 7.9
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# P值为2.8e-05,可认为四个厂生产的产品的变化率有显著差异
# 国内产品与国外产品有无显著差异? 将国内产品看做一类,国外产品看做另一类
df2 <- data.frame(X = c(20, 18, 19, 17, 15, 16, 13, 18, 22, 17, 26, 19, 26,
28, 23, 25, 24, 25, 18, 22, 27, 24, 12, 14), A = factor(rep(1:2, c(22, 2))))
fit.aov2 <- aov(X ~ A, data = df2)
summary(fit.aov2)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 1 117 117.3 6.69 0.017 *
## Residuals 22 386 17.5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# p值为0.017,可认为国内产品与国外产品有显著差异
# 国内各厂家的产品有无显著差异?
fit.aov3 <- aov(X ~ A, data = df[df$A != 4, ])
summary(fit.aov3)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 2 229 114.3 14 0.00018 ***
## Residuals 19 155 8.2
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# p值为0.00018,可认为国内各厂家的产品有显著差异
7.3某单位在大白鼠营养试验中,随机将大白鼠分为三组,测得每组12只大白鼠尿中氨氮的排出量(X(mg/6d)),数据由表7.27所示,试对该资料做正态性检验和方差齐性检验。
表7.27 白鼠尿中氨氮检测数据
| 白鼠 |
大白鼠营养试验中各组大鼠尿氨氮排出量(X(mg/6d)) |
| 第一组 |
� 30 27 35 35 29 33 32 36 26 41 33 31 |
| 第二组 |
� 43 45 53 44 51 53 54 37 47 57 48 42 |
| 第三组 |
� 82 66 66 86 56 52 76 83 72 73 59 53 |
rat <- data.frame(X = c(30, 27, 35, 35, 29, 33, 32, 36, 26, 41, 33, 31, 43,
45, 53, 44, 51, 53, 54, 37, 47, 57, 48, 42, 82, 66, 66, 86, 56, 52, 76,
83, 72, 73, 59, 53), A = factor(rep(1:3, c(12, 12, 12))))
# 做正态性检验
shapiro.test(rat$X[rat$A == 1])
##
## Shapiro-Wilk normality test
##
## data: rat$X[rat$A == 1]
## W = 0.9731, p-value = 0.9407
shapiro.test(rat$X[rat$A == 2])
##
## Shapiro-Wilk normality test
##
## data: rat$X[rat$A == 2]
## W = 0.9708, p-value = 0.9193
shapiro.test(rat$X[rat$A == 3])
##
## Shapiro-Wilk normality test
##
## data: rat$X[rat$A == 3]
## W = 0.9371, p-value = 0.4613
# 得到三组的p值均大于0.05,可认为数据在三个水平下均是正态分布
# 方差齐性检验,是检验数据在不同水平下方差是否相同
bartlett.test(X ~ A, data = rat) #bartlett.test(rat$x,rat$A) 效果相同
##
## Bartlett test of homogeneity of variances
##
## data: X by A
## Bartlett's K-squared = 12.14, df = 2, p-value = 0.002312
# p-value = 0.002312<0.05,因此可认为各组数据方差是不等的。
7.4 以小白鼠为对象研究正常肝核糖核酸(RNA)对癌细胞的生物作用,试验分别为对照组(生理盐水),水层RNA组和酚层RNA组,分别用此三种不同处理诱导肝癌细胞的果糖二磷酸酯酶(FDP酶)活力,数据如表7.28所示,问三种不同处理的诱导作用是否相同?
表7.28 三种不同处理的诱导结果
| 处理方法 |
诱导结果 |
| 对照组 |
2.79 2.69 3.11 3.47 1.77 2.44 2.83 2.52 |
| 水层RNA |
� 3.83 3.15 4.70 3.97 2.03 2.87 3.65 5.09 |
| 酚层RNA |
� 5.41 3.47 4.92 4.07 2.18 3.13 3.77 4.26 |
rat <- data.frame(X = c(2.79, 2.69, 3.11, 3.47, 1.77, 2.44, 2.83, 2.52, 3.83,
3.15, 4.7, 3.97, 2.03, 2.87, 3.65, 5.09, 5.41, 3.47, 4.92, 4.07, 2.18, 3.13,
3.77, 4.26), A = factor(rep(1:3, c(8, 8, 8))))
fit.aov <- aov(X ~ A, data = rat)
summary(fit.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 2 6.44 3.22 4.28 0.028 *
## Residuals 21 15.78 0.75
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 可认为三组的作用不相同
plot(rat$X ~ rat$A)

# 从图中可以可以看出,第一组显著低于第二和第三组
7.5 为研究人们在催眠状态下对各种情绪的反应十分有差异,选取了8个受试者,在催眠状态下,要求每人按任意次序作出恐惧、愉快、忧虑和平静4中反映。表7.29给出了各受试者在处于这4中清醒状态下皮肤的电位变化值,试在(alpha=0.05)下,检验受试者在催眠状态下对这4种情绪的反应力是否有显著差异。
表7.29:4种情绪状态下皮肤的电位变化值(单位: (mV))
| 情绪状态 |
受试者 |
|
1 2 3 4 5 6 7 8 |
| 恐惧 |
23.1 57.6 10.5 23.6 11.9 54.6 21.0 20.3 |
| 愉快 |
22.7 53.2 9.7 19.6 13.8 47.1 13.6 23.6 |
| 忧虑 |
22.5 53.7 10.8 21.1 13.7 39.2 13.7 16.3 |
| 平静 |
22.6 53.1 8.3 21.6 13.3 37.0 14.8 14.8 |
X = c(23.1, 57.6, 10.5, 23.6, 11.9, 54.6, 21, 20.3, 22.7, 53.2, 9.7, 19.6, 13.8,
47.1, 13.6, 23.6, 22.5, 53.7, 10.8, 21.1, 13.7, 39.2, 13.7, 16.3, 22.6,
53.1, 8.3, 21.6, 13.3, 37, 14.8, 14.8)
g <- gl(4, 8) #分为三组,每组8个
b <- gl(8, 1, 32) #每组内又有8个人,有顺序
friedman.test(X, g, b)
##
## Friedman rank sum test
##
## data: X, g and b
## Friedman chi-squared = 6.45, df = 3, p-value = 0.09166
# p-value = 0.09166>0.05,接受原假设,可认为四种情绪的反应力无显著差异
7.6 为了提高化工厂的产品质量,需要寻求最优反应温度与反应压力的配合,为此选择如下水平:
A:反应温度((^0C)) 60 70 80
B:反应压力(公斤) 2 2.5 3
在每个(A_iB_j)条件下做两次试验,其产量如表7.30所示
(1)对数据作方差分析(应考虑交互作用)
(2)求最优条件下平均产量的点估计和区间估计
(3)对(A_iB_j)条件下平均产量作多重比较。
表7.30 试验数据
|
(A_1) |
(A_2) |
(A_3) |
| (B_1) |
4.6 4.3 |
6.1 6.5 |
6.8 6.4 |
| (B_2) |
6.3 6.7 |
3.4 3.8 |
4.0 3.8 |
| (B_3) |
4.7 4.3 |
3.9 3.5 |
6.5 7.0 |
product <- data.frame(X = c(4.6, 4.3, 6.1, 6.5, 6.8, 6.4, 6.3, 6.7, 3.4, 3.8,
4, 3.8, 4.7, 4.3, 3.9, 3.5, 6.5, 7), A = gl(3, 2, 18), B = gl(3, 6, 18))
# 首先应该对数据做不同水平下的正态性检验,和各水平的方差齐性检验
# 对数据作方差分析(应考虑交互作用)
product.aov <- aov(X ~ A + B + A:B, data = product)
summary(product.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 2 4.44 2.22 29.8 0.00011 ***
## B 2 3.97 1.99 26.7 0.00016 ***
## A:B 4 21.16 5.29 71.1 8.3e-07 ***
## Residuals 9 0.67 0.07
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 可以看出,因素A和B,及其交互因素对产品质量有显著影响
# 求最优条件下平均产量的点估计和区间估计 计算两个因素在不同条件下的均值
tapply(product$X, product$A, mean)
## 1 2 3
## 5.150 4.533 5.750
tapply(product$X, product$B, mean)
## 1 2 3
## 5.783 4.667 4.983
# 可以看到在A3和B1条件,为最优条件
product.best <- c(6.8, 6.4)
# 均值的点估计为
mean(product.best)
## [1] 6.6
# 均值的区间估计为
t.test(product.best, alternative = c("two.sided"))
##
## One Sample t-test
##
## data: product.best
## t = 33, df = 1, p-value = 0.01929
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 4.059 9.141
## sample estimates:
## mean of x
## 6.6
# 对$A_iB_j$条件下平均产量作多重比较
TukeyHSD(product.aov)
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = X ~ A + B + A:B, data = product)
##
## $A
## diff lwr upr p adj
## 2-1 -0.6167 -1.0565 -0.1768 0.0089
## 3-1 0.6000 0.1602 1.0398 0.0104
## 3-2 1.2167 0.7768 1.6565 0.0001
##
## $B
## diff lwr upr p adj
## 2-1 -1.1167 -1.5565 -0.6768 0.0002
## 3-1 -0.8000 -1.2398 -0.3602 0.0017
## 3-2 0.3167 -0.1232 0.7565 0.1653
##
## $`A:B`
## diff lwr upr p adj
## 2:1-1:1 1.85 0.7706 2.9294 0.0015
## 3:1-1:1 2.15 1.0706 3.2294 0.0005
## 1:2-1:1 2.05 0.9706 3.1294 0.0007
## 2:2-1:1 -0.85 -1.9294 0.2294 0.1557
## 3:2-1:1 -0.55 -1.6294 0.5294 0.5677
## 1:3-1:1 0.05 -1.0294 1.1294 1.0000
## 2:3-1:1 -0.75 -1.8294 0.3294 0.2502
## 3:3-1:1 2.30 1.2206 3.3794 0.0003
## 3:1-2:1 0.30 -0.7794 1.3794 0.9600
## 1:2-2:1 0.20 -0.8794 1.2794 0.9965
## 2:2-2:1 -2.70 -3.7794 -1.6206 0.0001
## 3:2-2:1 -2.40 -3.4794 -1.3206 0.0002
## 1:3-2:1 -1.80 -2.8794 -0.7206 0.0019
## 2:3-2:1 -2.60 -3.6794 -1.5206 0.0001
## 3:3-2:1 0.45 -0.6294 1.5294 0.7612
## 1:2-3:1 -0.10 -1.1794 0.9794 1.0000
## 2:2-3:1 -3.00 -4.0794 -1.9206 0.0000
## 3:2-3:1 -2.70 -3.7794 -1.6206 0.0001
## 1:3-3:1 -2.10 -3.1794 -1.0206 0.0006
## 2:3-3:1 -2.90 -3.9794 -1.8206 0.0000
## 3:3-3:1 0.15 -0.9294 1.2294 0.9995
## 2:2-1:2 -2.90 -3.9794 -1.8206 0.0000
## 3:2-1:2 -2.60 -3.6794 -1.5206 0.0001
## 1:3-1:2 -2.00 -3.0794 -0.9206 0.0008
## 2:3-1:2 -2.80 -3.8794 -1.7206 0.0001
## 3:3-1:2 0.25 -0.8294 1.3294 0.9857
## 3:2-2:2 0.30 -0.7794 1.3794 0.9600
## 1:3-2:2 0.90 -0.1794 1.9794 0.1219
## 2:3-2:2 0.10 -0.9794 1.1794 1.0000
## 3:3-2:2 3.15 2.0706 4.2294 0.0000
## 1:3-3:2 0.60 -0.4794 1.6794 0.4737
## 2:3-3:2 -0.20 -1.2794 0.8794 0.9965
## 3:3-3:2 2.85 1.7706 3.9294 0.0001
## 2:3-1:3 -0.80 -1.8794 0.2794 0.1980
## 3:3-1:3 2.25 1.1706 3.3294 0.0003
## 3:3-2:3 3.05 1.9706 4.1294 0.0000
# 3-2 0.3167 -0.1232 0.7565 0.1653 表示因素B的3和2差异不显著 A:B
# 的比较类似,p值大于0.05的均可以认为扎伊不显著
7.7 某良种繁殖场为了提高水稻产量,指定试验的因素如表7.31所示。试选择(L_9(3^4))正交表安排试验,假定相应的产量为(单位:(kg/100m^2))62.925,57.075,51.6,55.05,58.05,56.55,63.225,50.7, 54.45。试对试验结果进行方差分析,并给出一组较好的种植条件
表7.31 水稻的试验因素水平表
| 因素 |
|
水平 |
|
|
1 |
2 |
3 |
| 品种 |
窄叶青8号 |
南二矮5号 |
珍珠矮11号 |
| 密度 |
4.50棵/100(m^2) |
3.75棵/100(m^2) |
3.00棵/100(m^2) |
| 施肥量 |
0.75(kg/100m^2) |
0.375(kg/100m^2) |
1.125(kg/100m^2) |
设三个因素为A(品种),B(密度),C(施肥量),采用(L_9(3^4))正交表安排试验,将ABC放到前三列,得到试验结果表
| 试验号 |
A(品种) |
B(密度) |
C(施肥量) |
产量 |
| 1 |
1 |
1 |
1 |
62.925 |
| 2 |
1 |
2 |
2 |
57.075 |
| 3 |
1 |
3 |
3 |
51.6 |
| 4 |
2 |
1 |
2 |
55.05 |
| 5 |
2 |
2 |
3 |
58.05 |
| 6 |
2 |
3 |
1 |
56.55 |
| 7 |
3 |
1 |
3 |
63.225 |
| 8 |
3 |
2 |
1 |
50.7 |
| 9 |
3 |
3 |
2 |
54.45 |
rice <- data.frame(A = gl(3, 3), B = gl(3, 1, 9), C = factor(c(1, 2, 3, 2, 3,
1, 3, 1, 2)), Y = c(62.925, 57.075, 51.6, 55.05, 58.05, 56.55, 63.225, 50.7,
54.45))
# 计算三个因素下产量的均值
tapply(rice$Y, rice$A, mean)
## 1 2 3
## 57.20 56.55 56.12
tapply(rice$Y, rice$B, mean)
## 1 2 3
## 60.40 55.27 54.20
tapply(rice$Y, rice$C, mean)
## 1 2 3
## 56.73 55.52 57.62
#
# 可见,A取2,B取1,C取3时,达到最优条件。即最有种植条件为,品种:南二矮5号;密度:4.50棵/100$m^2$;施肥量:1.125$kg/100m^2$
# 做无交互作用方差分析
rice.aov <- aov(Y ~ A + B + C, data = rice)
summary(rice.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 2 1.8 0.9 0.02 0.98
## B 2 65.9 32.9 0.84 0.54
## C 2 6.7 3.3 0.08 0.92
## Residuals 2 78.8 39.4
# 发现ABC对结果的影响均不显著
7.8 某单位研究四种因素对钉螺产卵数(Y)的影响,制定试验的因素如表7.32所示,试选择(L_8(2^7))正交表安排试验,假定相应的钉螺产卵数为(单位:个),86,95,91,94,91,96,83,88,试对试验结果进行方差分析,并给出一组较好的灭螺方案(考虑有交互作用)。
表7.32 钉螺产卵影响试验因素的水平表
| 因素 |
|
水平 |
|
1 |
2 |
| 温度(A) |
5(^0C) |
10(^0C) |
| 含氧量(B) |
0.5 |
5.0 |
| 含水量(C) |
10% |
30% |
| pH值(D) |
6.0 |
8.0 |
设四个因素为温度(A),含氧量(B),含水量(C),pH值(D),采用(L_8(2^7))两列间交互作用的正交表安排试验,第1列放A,第2列放B,第3列放A×B,第4列放C,第5列A×C,第6列B×C,第7列D,得到试验结果表
| 试验号 |
温度(A) |
含氧量(B) |
A×B |
含水量(C) |
A×C |
B×C |
pH值(D) |
钉螺产卵数 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
86 |
| 2 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
95 |
| 3 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
91 |
| 4 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
94 |
| 5 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
91 |
| 6 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
96 |
| 7 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
83 |
| 8 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
88 |
insect <- data.frame(A = gl(2, 4), B = gl(2, 2, 8), C = gl(2, 1, 8), D = factor(c(1,
2, 2, 1, 2, 1, 1, 2)), Y = c(86, 95, 91, 94, 91, 96, 83, 88))
# 计算四个个因素下钉螺产卵数的均值
tapply(insect$Y, insect$A, mean)
## 1 2
## 91.5 89.5
tapply(insect$Y, insect$B, mean)
## 1 2
## 92 89
tapply(insect$Y, insect$C, mean)
## 1 2
## 87.75 93.25
tapply(insect$Y, insect$D, mean)
## 1 2
## 89.75 91.25
#
# 温度(A)取水平2,含氧量(B)取水平2,含水量(C)取水平1,pH值(D)取水平1,此时钉螺产卵数最少
# 做有交互作用方差分析
insect.aov <- aov(Y ~ A + B + A:B + C + A:C + B:C + D, data = insect)
summary(insect.aov)
## Df Sum Sq Mean Sq
## A 1 8.0 8.0
## B 1 18.0 18.0
## C 1 60.5 60.5
## D 1 4.5 4.5
## A:B 1 50.0 50.0
## A:C 1 0.5 0.5
## B:C 1 4.5 4.5
# 发现ABCD及其交互作用,对结果的影响均不显著,去掉Sum
# Sq最大的三个因素B,C,A:B
insect.aov <- aov(Y ~ A + A:C + B:C + D, data = insect)
summary(insect.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 1 8.0 8.0 0.16 0.76
## D 1 4.5 4.5 0.09 0.81
## A:C 2 61.0 30.5 0.61 0.67
## C:B 2 22.5 11.3 0.23 0.83
## Residuals 1 50.0 50.0
# 可看出各因素及其交互因素对钉螺产卵数无显著影响
7.9 某工厂为了提高零件内孔研磨工序质量进行工艺的参数优选试验,考察孔的锥度值,希望其越小越好,在试验中考察因子的水平表7.33,试选择(L_8(2^7))正交表安排试验,其表头设计如表7.34所示,在每一条件下加工了四个零件,测量其锥度,试验结果如表7.35所示,试对试验结果进行方差分析,并给出一组较好的工艺参数指标。
表7.33 因子水平表
| 因素 |
水平 |
|
|
1 |
2 |
| 研孔工艺设备(A) |
通用夹具 |
专用夹具 |
| 生铁研圈材质(B) |
特殊铸铁 |
一般灰铸铁 |
| 留研量(mm)(C) |
0.01 |
0.015 |
表7.34 试验结果
|
|
|
|
|
|
|
|
| 表头设计 |
A |
B |
--- |
C |
--- |
--- |
--- |
| 列号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
表7.35 试验结果
| 试验号 |
试验值 |
| 1 |
1.5 1.7 1.3 1.5 |
| 2 |
1.0 1.2 1.0 1.0 |
| 3 |
2.5 2.2 3.2 2.0 |
| 4 |
2.5 2.5 1.5 2.8 |
| 5 |
1.5 1.8 1.7 1.5 |
| 6 |
1.0 2.5 1.3 1.5 |
| 7 |
1.8 1.5 1.8 2.2 |
| 8 |
1.9 2.6 2.3 2.0 |
选择(L_8(2^7))正交表安排试验,ABC分别放到124列
| 试验号 |
A |
B |
C |
试验值 |
| 1 |
1 |
1 |
1 |
1.5 1.7 1.3 1.5 |
| 2 |
1 |
1 |
2 |
1.0 1.2 1.0 1.0 |
| 3 |
1 |
2 |
1 |
2.5 2.2 3.2 2.0 |
| 4 |
1 |
2 |
2 |
2.5 2.5 1.5 2.8 |
| 5 |
2 |
1 |
1 |
1.5 1.8 1.7 1.5 |
| 6 |
2 |
1 |
2 |
1.0 2.5 1.3 1.5 |
| 7 |
2 |
2 |
1 |
1.8 1.5 1.8 2.2 |
| 8 |
2 |
2 |
2 |
1.9 2.6 2.3 2.0 |
# 有重复试验的方差分析
hole <- data.frame(A = gl(2, 4, 32), B = gl(2, 2, 32), C = gl(2, 1, 32), Y = c(1.5,
1, 2.5, 2.5, 1.5, 1, 1.8, 1.9, 1.7, 1.2, 2.2, 2.5, 1.8, 2.5, 1.5, 2.6, 1.3,
1, 3.2, 1.5, 1.7, 1.3, 1.8, 2.3, 1.5, 1, 2, 2.8, 1.5, 1.5, 2.2, 2))
hole.aov <- aov(Y ~ A + B + C, data = hole)
summary(hole.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## A 1 0.01 0.01 0.04 0.84
## B 1 4.73 4.73 24.06 3.6e-05 ***
## C 1 0.04 0.04 0.19 0.66
## Residuals 28 5.50 0.20
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 可以看出因素B对实验结果影响显著 计算三个因素下钉螺产卵数的均值
tapply(hole$Y, hole$A, mean)
## 1 2
## 1.837 1.806
tapply(hole$Y, hole$B, mean)
## 1 2
## 1.438 2.206
tapply(hole$Y, hole$C, mean)
## 1 2
## 1.856 1.788
# 因此最优的工艺参数指标为A1,B2,C1

