最近在备战软考,复习到计算机组成原理的时候,看到书中关于原码、反码、补码和移码的定义如下(n是机器字长):
原码:
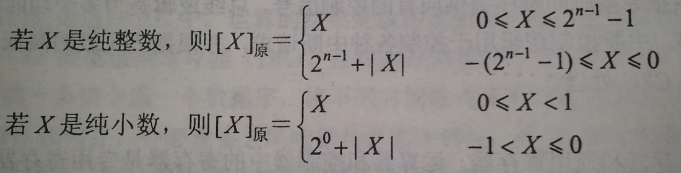
反码:
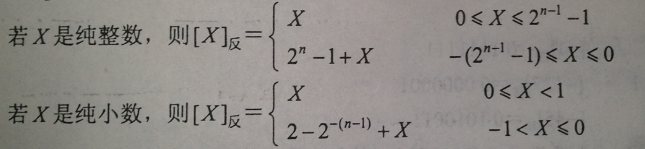
补码:
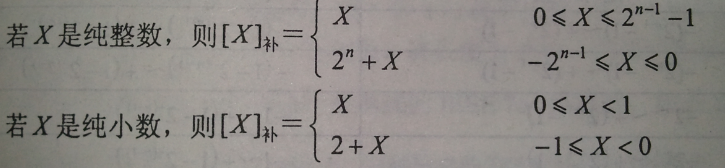
移码:
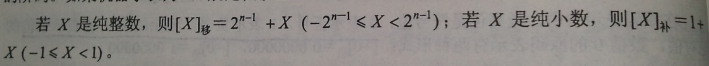
看完这些定义以后,我的脑袋瞬间膨胀到原来的二倍!这样变态的公式不管你记不记得住,反正我是记不住!还好以前对它们有所了解,否则看到这一堆公式恐怕我早就放弃参加软考的念头喽。
其实没必要弄得这么麻烦,它们完全可以用一两句话就描述的很清楚。
原码:
如果机器字长为n,那么一个数的原码就是用一个n位的二进制数,其中最高位为符号位:正数为0,负数为1。剩下的n-1位表示概数的绝对值。
例如: X=+101011 , [X]原= 00101011 X=-101011 , [X]原= 10101011
位数不够的用0补全。
PS:正数的原、反、补码都一样:0的原码跟反码都有两个,因为这里0被分为+0和-0。
反码:
知道了什么是原码,那反码就更是张飞吃豆芽——小菜一碟了。知道了原码,那么你只需要具备区分0跟1的能力就可以轻松求出反码,为什么呢?因为反码就是在原码的基础上,符号位不变其他位按位取反(就是0变1,1变0)就可以了。
例如:X=-101011 , [X]原= 10101011 ,[X]反=11010100
补码:
补码也非常的简单就是在反码的基础上按照正常的加法运算加1。
例如:X=-101011 , [X]原= 10101011 ,[X]反=11010100,[X]补=11010101
PS:0的补码是唯一的,如果机器字长为8那么[0]补=00000000。
移码:
移码最简单了,不管正负数,只要将其补码的符号位取反即可。
例如:X=-101011 , [X]原= 10101011 ,[X]反=11010100,[X]补=11010101,[X]移=01010101