- SleepyBag的回答 - 知乎 https://www.zhihu.com/question/30269898/answer/1374596782
链接:https://www.zhihu.com/question/30269898/answer/1374596782
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
假如你在做一个抛硬币实验。硬币朝上的概率是 p,但是你不知道具体是多少,你想通过实验确定 p。
你做了 A + B 次实验,抛出 A 次正面,B 次反面。请问 p 是多少?
什么?你说 ?
太不专业了吧,我们是统计科学家,什么事情都要看个概率。
最符合我们的实验结果,固然可能性最大,但是我们也不能忽略其他取值的可能性。
比如说吧,如果说 ,那我们能不能扔出 A 次正面,B 次反面?可能啊,而且可能性很大,如果
,那我们的实验结果也几乎完全符合预期。再比如说,就算
,那我们扔出 10 次正面,0 次反面,有没有可能?好像也有可能,只是可能性很小。
看到没有,这个 p 始终有可能是 0 到 1 当中的任何一个值。而当我们观测到 A 次正面,B 次反面之后,能做的只是给它一个概率分布,就像上面说的, 的可能性很大,而
的可能性很小。
那么,这个概率分布到底是什么呢?有的同学可能知道了,就是贝塔分布。
但是先别急着看结论。这个问题其实并不难,我们先来自己动手算一下,实践出真知:
我们在对这个硬币一无所知的情况下,认为 是 0 到 1 的任何值都是等可能的。因此,在观测到一些实验结果之后,我们可以按照极大似然估计的思想 —— 参数
下我的实验结果的可能性,就是参数
的靠谱程度——得到参数
的分布。
假设这个硬币出正面的概率是 ,我们一共做了 A + B 次实验,那么我们得到 A 次正面的概率可以简单地算出来,从 A + B 次实验里面有 A 个正面的情况数量是
,每个情况的出现概率是
。综合起来,A 次正面的概率是:
这个概率 就是所谓“参数
下我的实验结果的可能性”,同时也是
的靠谱程度,也就是似然。
那么我们把 的靠谱程度做成函数,其实就是把上面等号左边的形式改一下:
然后我们把这个靠谱程度的函数归一化一下,让它的积分为 1,变成一个概率分布。直观上看,要把一个正函数变成一个概率分布,就是要让函数的图像面积为 1. 所以做法就是给这个函数除以它的图像面积,也就是这个函数的积分。于是就有:
你如果知道 Beta 分布的公式的话,相信你已经看出来怎么回事了。我们得到的,其实就是 Beta 分布的概率密度函数。下面我把维基百科的 Beta 分布密度函数粘贴过来,同学们可以对比一下:
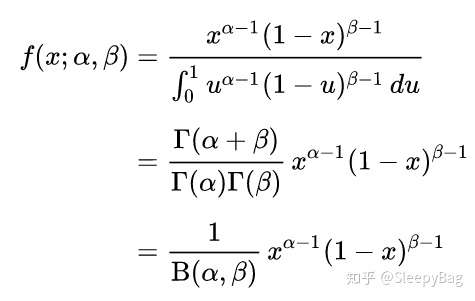
Beta 分布的 x,就是我们要估计的 ,也就是这枚硬币正面朝上的概率。
就是我们的 A + 1,
就是我们的 B + 1,也就是代表我们已经观测到的正面/背面朝上的次数。至于为什么差个 1,可能只是为了
与
函数的简洁。
那么我们总结一下,什么叫 Beta 分布?
所谓的以 为参数的 Beta 分布
,其实描述的就是我们在做抛硬币实验的过程中,我们当前如果已经观测到
次正面,
次反面,那么此时硬币正面朝上的真实概率的可能性分布。