一、定义
左式堆是为了有效的支持合并操作(merge),将2个堆进行合并,不只是合并2个数组,还要维护其中的堆结构。左式堆像二叉堆那样具有结构性和有序性。也有堆序性质,也是二叉树,但它不是平衡的,而是趋向于非常不平衡。
1.1 一些特点和定义
我们为左式堆做如下定义:
-
零路径长(npl):任意节点X到一个不具有2个儿子的节点的最短路径长;
-
具有0个儿子或1个儿子的节点的npl为0;
-
npl(null)= -1;
根据以上定义可知,任意节点的npl比它各个儿子节点的npl的最小值大1,这个节点也是用少于2个儿子的节点,因为null的npl定义为-1。
二、性质
对于堆中的每一个节点X,左儿子的零路径长至少与右儿子的零路径长相等。
图解: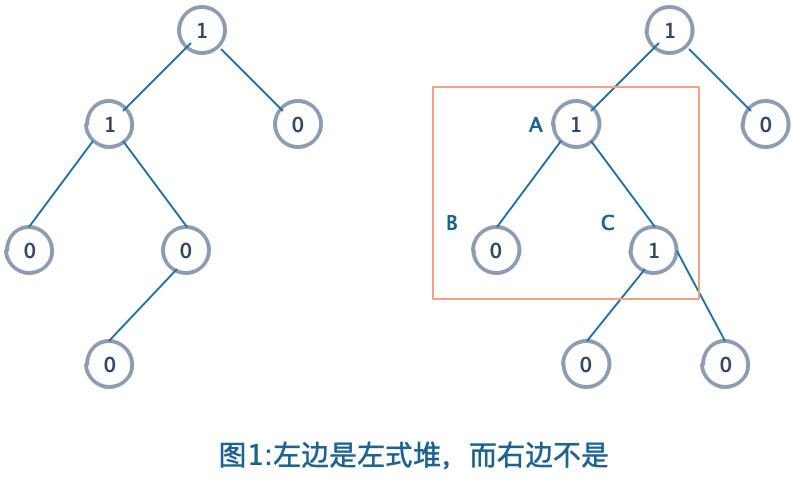
如上图1,在右图中,红色框中的子节点B和子节点C,作为左儿子的B节点的npl是0,而作为右儿子的C节点npl是1,并不满足左式堆的性质。
左式堆的性质趋向于加深左路径,所以右路径应该短,事实上,沿着左式堆的右侧的右路径确实是该堆中最短的路径。否则就会破坏左式堆的性质。
左式堆的性质,就是不平衡的,显然它就是为了让树往左边加深。这样做更利于合并,正因如此,我们定义它为左式堆。
定理一:在右路径上有r个节点的左式树必定有(2^r -1) 个节点。
右路径:节点的右儿子的右儿子的右儿子的右儿子的右儿子组成的路径….就是一只往右儿子下去。
数学归纳法:
r = 1时,必然存在一个节点,至少存在根节点,也许有左节点。
r = 2时,右一个右儿子,那么根据左式堆性质,必然存在一个左儿子。节点(N ge 3)(根节点+左儿子+右儿子)。
r = 3时,r = 4时…..只要满足二叉堆的性质。那么子树必定大于右子树的节点数目。很容易就能得到规律。
三、操作
对左式堆最基础也是最重要的操作就是合并
3.1 合并(merge)
说明:
- 插入是简单的合并,看作一个左式堆与另一个节点数等于1的左式堆的合并。
- 合并空堆不需要操作,直接返回非空的堆作为结果。
- 最后得到的堆也是左式堆。
过程图解:
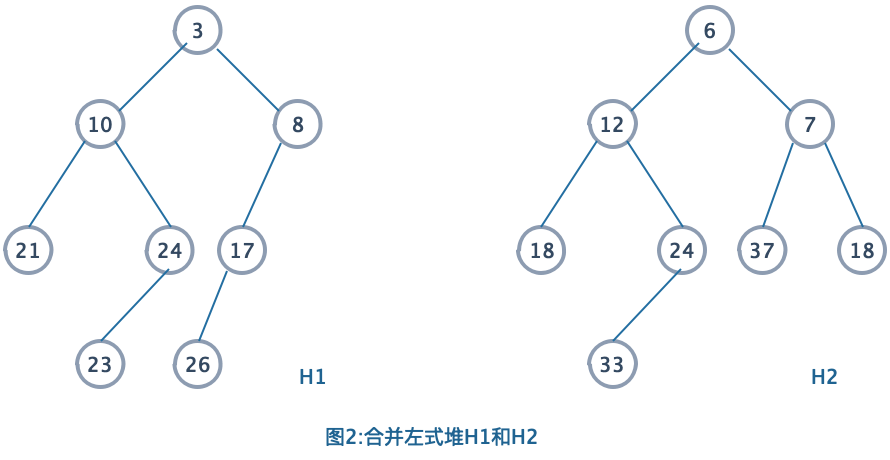

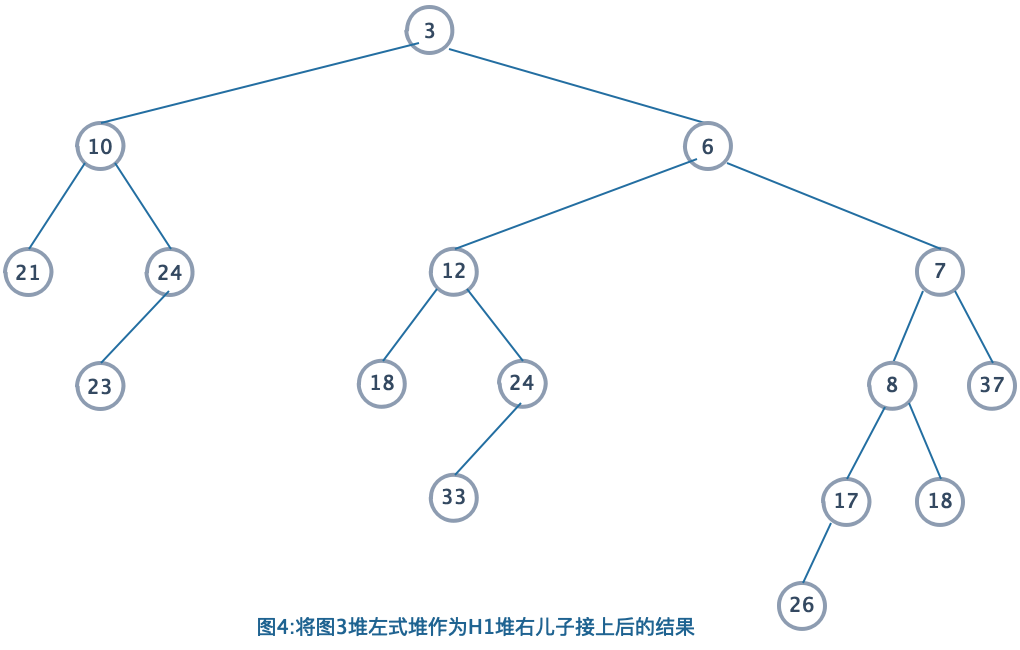
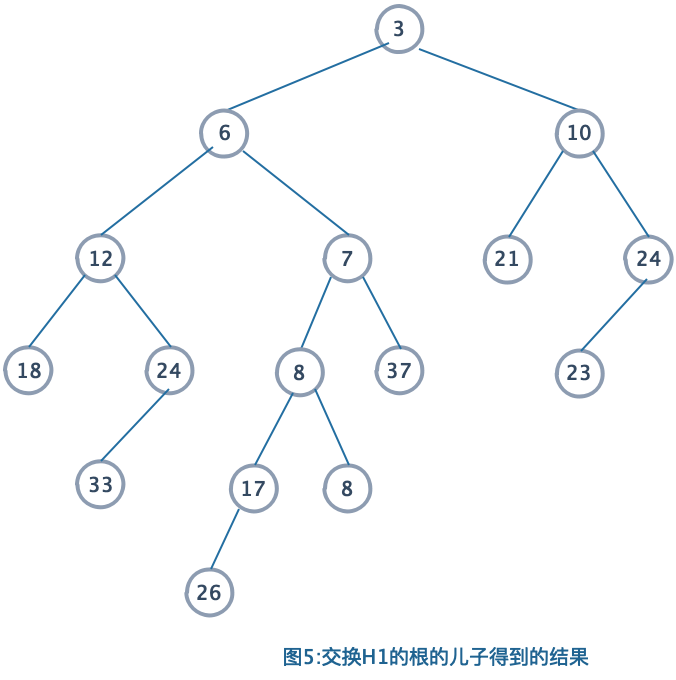
过程描述:
-
我们递归的将H1的右子堆(节点8)和H2合并,得到图3。(根据递归法则,我们把一棵树是空的时候作为基准情形,能处理基准情形自然能递归完成)
-
我们将图3的结果作为H1的右子堆,得到图4。(满足堆序性质,但是不满足左式堆性质)
-
我们将图4的结果的堆的左右子树交换,得到图5,(是个左式堆)
递归法则:
1.基准情形。必须总要有某些基准情形,它无需递归就能解出。
2.不断推进。对于那些需要递归求解的情形,每一次递归调用都必须要使状况朝向一种基准情形推进。
3.设计法则。假设所有的递归调用都能运行。
4.合成效益法则(compound interest rule)。在求解一个问题的同一实例时,切勿在不同的递归调用中做重复性的工作。
结果分析:
执行合并的时间与诸右路径的长的和成正比,因为在递归调用期间对每一个被访问的节点花费的是常数工作量。因此,我们得到合并两个左式堆的时间界为(O(logN))。
关于时间界(O(logN)):
二叉树的访问时间为(O(logN)),这是为什么呢,很明显,(logN)为二叉树的高,二叉树本来就是一层层寻找,所以得到这个时间界。而堆作为二叉树的一种,递归的操作是循环访问树节点,根据递归法则4,不存在重复的情况下, 访问节点时间就是(O(logN))。
代码地址
https://github.com/dhcao/dataStructuresAndAlgorithm/blob/master/src/chapterSix/LeftistHeap.java