python语言绘图：绘制贝叶斯方法中最大后验密度（Highest Posterior Density, HPD）区间图的近似计算

代码源自:

https://github.com/PacktPublishing/Bayesian-Analysis-with-Python

===========================================================

贝叶斯方法中最大后验密度（Highest Posterior Density, HPD）区间，是指包含一定比例概率密度的最小区间。

百科的解释：https://baike.baidu.com/item/%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%8C%BA%E9%97%B4%E4%BC%B0%E8%AE%A1/1498732?fr=aladdin

主要判断所得的区间是否为HPD的依据为：

===========================================================

 

 

 

 

 

 

 

由上述信息可以知道HPD在离散分布时是难以计算的，但是实际上即使是连续分布时也是很难计算的，下面分情况讨论一下。

 

 

 

 

• 当概率分布为单峰分布时，如果分布为左右对称那么这个HPD是很好计算的，其中最典型的代表就是高斯分布。此时的HPD区间就等于频率学派的置信区间。

 

 

 

 

• 当概率分布为单峰分布时，如果分布为左右不是完全对称的那么这个HPD就很难计算，此时我们可以假设这个不对称的分布可以近似于一个对称的分布，其中比较典型的代表就是beta分布，不过这里需要知道既然是近似就一定存在偏差，而这个偏差随着不对称程度的增加而增加。既然我们这里把单峰不对称分布假设近似于单峰对称分布，自然我们采用的HPD方法类似于单峰对称分布。

例子：求beta(5, 11)分布的95%的HPD区间，即计算概率密度函数为2.5%和97.5%的自变量区间

 1. 直接根据密度函数的反函数进行计算

 

from scipy import stats
print(stats.beta(5, 11).ppf(0.025), stats.beta(5, 11).ppf(0.975))

 

 

 2. 根据蒙特卡洛模拟，对分布进行一定数量的采样（如10000次），此时的采样数据可以看做是自变量分布的近似，此时求出这些采样数据的百分位数为2.5%和97.5%时对应的自变量的值，此时所获区间为HPD的近似区间。由于使用beta分布的概率密度函数为2.5%和97.5%的自变量区间本身就是对HPD的一种近似，而采用蒙特卡洛模拟求概率密度函数更是一种近似，这种多次近似的结果要差于前一种方法。

 

 代码：

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns
palette = 'muted'
sns.set_palette(palette); sns.set_color_codes(palette)


def naive_hpd(post):
    sns.kdeplot(post)
    HPD = np.percentile(post, [2.5, 97.5])
    plt.plot(HPD, [0, 0], label='HPD {:.2f} {:.2f}'.format(*HPD),
             linewidth=8, color='k')
    plt.legend(fontsize=16);
    plt.xlabel(r"$\theta$", fontsize=14)
    plt.gca().axes.get_yaxis().set_ticks([])


np.random.seed(1)
post = stats.beta.rvs(5, 11, size=1000)
naive_hpd(post)
plt.xlim(0, 1)
plt.savefig('B04958_01_07.png', dpi=300, figsize=(5.5, 5.5))

plt.show()

 绘图：

 

 

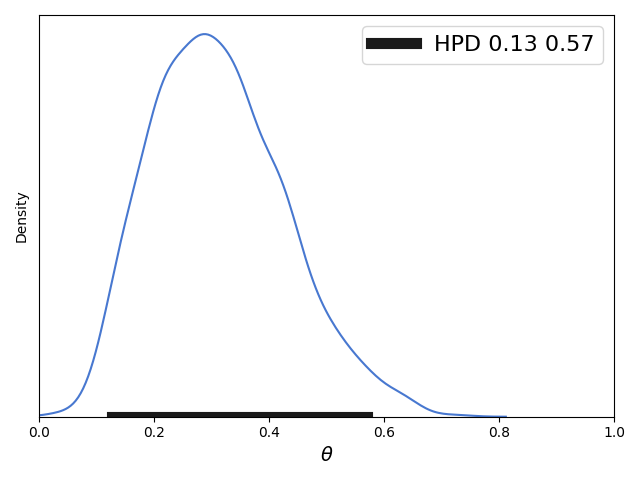
可以看到此时的区间[0.13, 0.57]距离[0.11824110336688091,  0.5510032410369705]还是存在一点偏差的，而这个偏差随着蒙特卡洛采样数据量的增加而减少，对此尝试代码如下：

import numpy as np
from scipy import stats
import seaborn as sns
palette = 'muted'
sns.set_palette(palette); sns.set_color_codes(palette)


np.random.seed(1)
for n in [10**3, 10**4, 10**5, 10**6, 10**7, 10**8, 10**9,]:
    post = stats.beta.rvs(5, 11, size=n)
    HPD = np.percentile(post, [2.5, 97.5])
    print(HPD)
    print(stats.beta(5,11).cdf(HPD[0]), stats.beta(5,11).cdf(HPD[1]))

运行结果：

 

 

 

 

==================================================================

 

 

 

 

 

 

 

以上的方法都是基于近似的，那么有没有精度更好的求解HPD的办法呢，给出下面的代码：

 

 

from scipy import stats
import seaborn as sns
palette = 'muted'
sns.set_palette(palette); sns.set_color_codes(palette)


a_per = 0.025
b_per = 0.975
ab_per = 0.95
alpha = 5
beta = 11

a = stats.beta(alpha, beta).ppf(a_per)
b = stats.beta(alpha, beta).ppf(b_per)

for i in range(10**8):
    a_p = stats.beta(alpha, beta).pdf(a)
    b_p = stats.beta(alpha, beta).pdf(b)

    print("{:6d} \t {:8f} {:8f} \t\t {:8f} {:8f}".format(i, a, b, a_p, b_p))

    if abs(a_p - b_p)<0.0001:
        break

    if a_p > b_p:
        a = a - 0.000001
    else:
        a = a + 0.000001
    b = stats.beta(alpha, beta).ppf( stats.beta(alpha, beta).cdf(a)+ab_per )

 

 

 

 

 

 

运行结果：

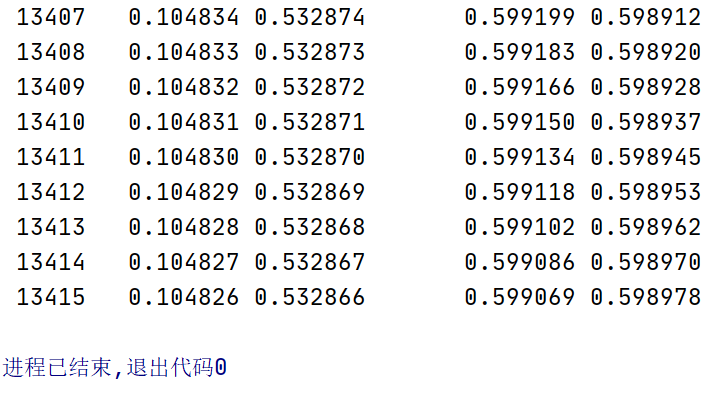
通过运行结果我们得到最后的区间为：

[0.104826, 0.532866]

可以看到这个区间结果与第一种方法的结果还是有一定差距的。

 

 

 

 

 

 

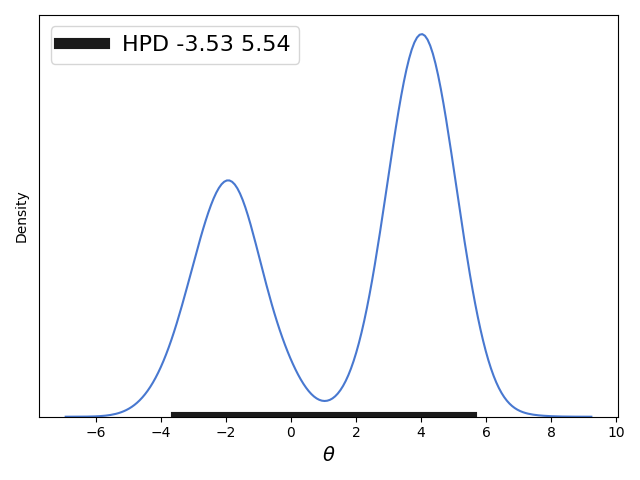
• 当概率分布为双峰分布时，并且HPD的区间包括在双峰的大部分并且双峰的外侧分布相似那么上面的第二种近似求解HPD区间的方式同样适用，但是其他的近似求解方式已经不适应了，因为对于很多双峰分布我们是难以写出具体的概率分布函数的。给出相应代码：

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns
palette = 'muted'
sns.set_palette(palette); sns.set_color_codes(palette)

def naive_hpd(post):
    sns.kdeplot(post)
    HPD = np.percentile(post, [2.5, 97.5])
    plt.plot(HPD, [0, 0], label='HPD {:.2f} {:.2f}'.format(*HPD),
      linewidth=8, color='k')
    plt.legend(fontsize=16);
    plt.xlabel(r"$\theta$", fontsize=14)
    plt.gca().axes.get_yaxis().set_ticks([])

np.random.seed(1)
gauss_a = stats.norm.rvs(loc=4, scale=0.9, size=3000)
gauss_b = stats.norm.rvs(loc=-2, scale=1, size=2000)
mix_norm = np.concatenate((gauss_a, gauss_b))

naive_hpd(mix_norm)
plt.savefig('B04958_01_08.png', dpi=300, figsize=(5.5, 5.5))

plt.show()

 

 

===============================================================