原地址:https://www.jiqizhixin.com/graph/technologies/56dbb21e-c3f9-4e06-b16a-2e28f25b26c8
===========================================
人机博弈是人工智能的重要分支,人们在这一领域探索的过程中产生了大量的研究成果,而极小化极大算法(minimax)是其中最基础的算法,它由Shannon在1950年正式提出。Alpha-beta剪枝的本质就是一种基于极小化极大算法的改进方法。在人机博弈中,双方回合制地进行走棋,己方考虑当自己在所有可行的走法中作出某一特定选择后,对方可能会采取的走法,从而选择最有利于自己的走法。这种对弈过程就构成了一颗博弈树,双方在博弈树中不断搜索,选择对自己最为有利的子节点走棋。在搜索的过程中,将取极大值的一方称为max,
===========================================
人机博弈是人工智能的重要分支,人们在这一领域探索的过程中产生了大量的研究成果,而极小化极大算法(minimax)是其中最基础的算法,它由Shannon在1950年正式提出。Alpha-beta剪枝的本质就是一种基于极小化极大算法的改进方法。
在人机博弈中,双方回合制地进行走棋,己方考虑当自己在所有可行的走法中作出某一特定选择后,对方可能会采取的走法,从而选择最有利于自己的走法。这种对弈过程就构成了一颗博弈树,双方在博弈树中不断搜索,选择对自己最为有利的子节点走棋。在搜索的过程中,将取极大值的一方称为max,取极小值的一方称为min。max总是会选择价值最大的子节点走棋,而min则相反。这就是极小化极大算法的核心思想。
极小化极大算法最大的缺点就是会造成数据冗余,而这种冗余有两种情况:①极大值冗余;②极小值冗余。相对应地,alpha剪枝用来解决极大值冗余问题,beta剪枝则用来解决极小值冗余问题,这就构成了完整的Alpha-beta剪枝算法。接下来对极大极小值冗余和具体剪枝过程作简要介绍。
极大值冗余如图1所示,这是一颗博弈树的某一部分,节点下的数据为该节点的值,节点B的值为20,节点D的值为15,这里,C为取极小值的min节点,因此节点C的值将小于等于15;而节点A为取最大值max的节点,因此A只可能取到B的值,也是就说不再需要搜索C的其他子节点E和F的值就可以得出节点A的值。这样将节点D的后继兄弟节点减去称为Alpha剪枝。
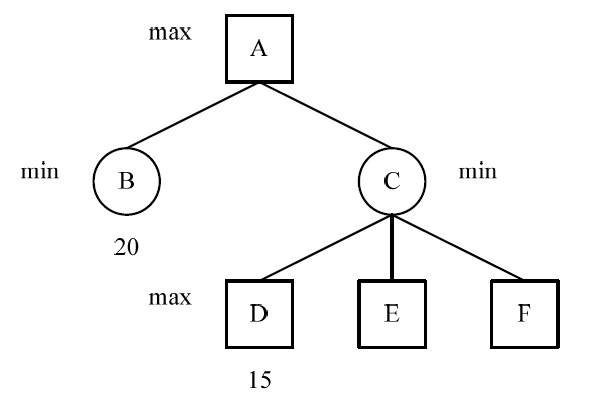
图 1 极大值冗余的Alpha剪枝
极小值冗余如图2所示,这也是一颗博弈树的某一部分,节点B的值为10,节点D的值为19,这里,C节点为取最大值max节点。因此,C的值将大于等于19;节点A为取极小值的min节点,因此A的值只能取B的值10,也就是说不再需要求节点C的子节点E和F的值就可以得出节点A的值。这样将节点D的后继兄弟节点减去称为Beta剪枝。
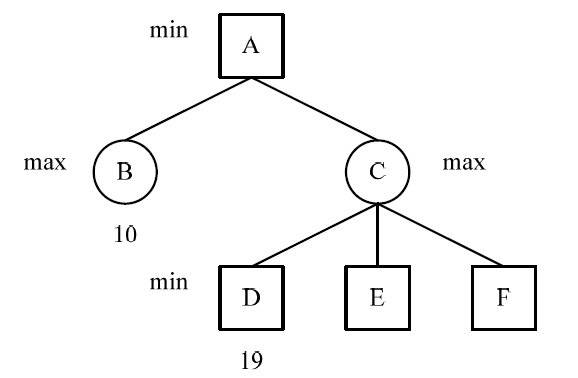
图2 极小值冗余的Beta剪枝
[描述来源:Shannon, C. E. (1950). XXII. Programming a computer for playing chess. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 41(314), 256-275.
URL:http://www.tandfonline.com/doi/pdf/10.1080/14786445008521796
描述来源:Knuth, D. E., & Moore, R. W. (1975). An analysis of alpha-beta pruning. Artificial intelligence, 6(4), 293-326.
URL:http://www.sciencedirect.com/science/article/pii/0004370275900193
描述来源:Su, Y. J. F. (2009). IMPROVEMENT ON ALPHA-BETA SEARCH ALGORITHM IN CHINESE CHESS [J]. Journal of Beijing Normal University (Natural Science), 2, 013.
URL:http://en.cnki.com.cn/Article_en/CJFDTotal-BSDZ200902013.htm]
===========================================
发展历史
Shannon在1950年提出了极小化极大算法,奠定了计算机博弈的理论基础。1955年,MacCarthy提出了类似Alpha-beta剪枝算法。此后,多名学者先后独立发现Alpha-beta算法并发表相关论文,比如Richards、Kotok和Brudno等人。Knuth等人在1975年优化了算法,提出了负极大值(negamax)概念,这一概念的原理本质上与极小化极大值算法并无不同,但是却不需要系统区分取极大值者和极小值者,使得算法更加统一。此外,Knuth等人也对alpha-beta剪枝算法的搜索效率进行了深入的研究,Pearl也在1982年证明了alpha-beta剪枝原理的最优性。
主要事件
| 年份 | 事件 | 相关论文 |
| 1950 | Shannon提出了极小化极大算法(minimax),奠定了计算机博弈的理论基础 | Shannon, C. E. (1950). XXII. Programming a computer for playing chess. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 41(314), 256-275. |
| 1955 | MacCarthy提出了类似Alpha-beta剪枝算法的思想 | McCarthy, J. (1955). Human-Level Ai Is Harder Than It Seemed. |
| 1961 | Richards和Hart独立提出alpha-beta剪枝原理 | Richards, D. J., & Hart, T. P. (1961). The alpha-beta heuristic. |
| 1975 | Knuth提出了负极大值(negamax)概念,并深入研究了alpha-beta算法的效率问题 | Knuth, D. E., & Moore, R. W. (1975). An analysis of alpha-beta pruning. Artificial intelligence, 6(4), 293-326. |
| 1976 | Newell和Simon使用了经过多次改造的alpha-beta剪枝算法 | Newell, A., & Simon, H. A. (1976). Computer science as empirical inquiry: Symbols and search. Communications of the ACM, 19(3), 113-126. |
| 1982 | Pearl证明了alpha-beta剪枝原理的最优性 | Pearl, J. (1982). The solution for the branching factor of the alpha-beta pruning algorithm and its optimality. Communications of the ACM, 25(8), 559-564. |
| 2012 | Saffidine等人提出了alpha-beta剪枝在博弈游戏中的一揽子解决方案。论文中首先对这类博弈游戏进行了泛化抽象,定义了这类游戏的一般框架,然后基于这些框架提出了通用的(general)解决方案。 | Saffidine, A., Finnsson, H., & Buro, M. (2012, July). Alpha-Beta Pruning for Games with Simultaneous Moves. In <i>AAAI</i>. |
发展分析
瓶颈
Alpha-beta剪枝本质是alpha剪枝和beta剪枝的结合,这两种剪枝的发生条件不同,因此在博弈中总是首先需要区分取极小值和取极大值方,这在一定程度上让算法的效率打了折扣。
未来发展方向
Alpha-beta剪枝是对极小化极大算法的一种改进,但是在实际应用过程中,alpha-beta剪枝首先要区分出博弈双方谁是取极大值者,谁是取极小值者,达到剪枝条件时才会进行剪枝。这一优化方法虽然简洁明了,但在一定程度上让算法的效率打了折扣。因此在具体的博弈中,结合博弈的特定规则进行优化,比如说,将一些先验知识(prior knowledge)纳入剪枝条件中,这种基于具体应用的优化将是alpha-beta剪枝的重要发展方向。
Contributor: Keyu Qi
===========================================
注明:个人补充
一个比较详细介绍具体过程的文章,个人感觉不错,易懂:
一图流解释 Alpha-Beta 剪枝(Alpha-Beta Pruning)
Alpha-Beta剪枝用于裁剪搜索树中不需要搜索的树枝,以提高运算速度。它基本的原理是:
- 当一个 Min 节点的 β值≤任何一个父节点的α值时 ,剪掉该节点的所有子节点
- 当一个 Max 节点的 α值≥任何一个父节点的β值时 ,剪掉该节点的所有子节点
下略,具体见: https://www.7forz.com/3211/
===========================================