【转载】 强化学习（一）模型基础

原文地址：

https://www.cnblogs.com/pinard/p/9385570.html

----------------------------------------------------------------------------------------

从今天开始整理强化学习领域的知识，主要参考的资料是Sutton的强化学习书和UCL强化学习的课程。这个系列大概准备写10到20篇，希望写完后自己的强化学习碎片化知识可以得到融会贯通，也希望可以帮到更多的人，毕竟目前系统的讲解强化学习的中文资料不太多。

　　　　第一篇会从强化学习的基本概念讲起，对应Sutton书的第一章和UCL课程的第一讲。

1.  强化学习在机器学习中的位置

强化学习的学习思路和人比较类似，是在实践中学习，比如学习走路，如果摔倒了，那么我们大脑后面会给一个负面的奖励值，说明走的姿势不好。然后我们从摔倒状态中爬起来，如果后面正常走了一步，那么大脑会给一个正面的奖励值，我们会知道这是一个好的走路姿势。那么这个过程和之前讲的机器学习方法有什么区别呢？

　　　　强化学习是和监督学习，非监督学习并列的第三种机器学习方法，从下图我们可以看出来。

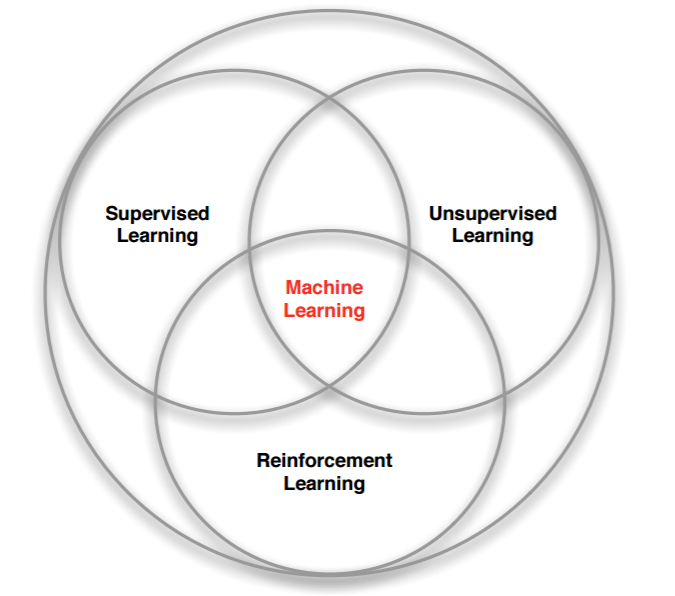
强化学习来和监督学习最大的区别是它是没有监督学习已经准备好的训练数据输出值的。强化学习只有奖励值，但是这个奖励值和监督学习的输出值不一样，它不是事先给出的，而是延后给出的，比如上面的例子里走路摔倒了才得到大脑的奖励值。同时，强化学习的每一步与时间顺序前后关系紧密。而监督学习的训练数据之间一般都是独立的，没有这种前后的依赖关系。

再来看看强化学习和非监督学习的区别。也还是在奖励值这个地方。非监督学习是没有输出值也没有奖励值的，它只有数据特征。同时和监督学习一样，数据之间也都是独立的，没有强化学习这样的前后依赖关系。

2. 强化学习的建模

　　　　我们现在来看看强化学习这样的问题我们怎么来建模，简单的来说，是下图这样的：

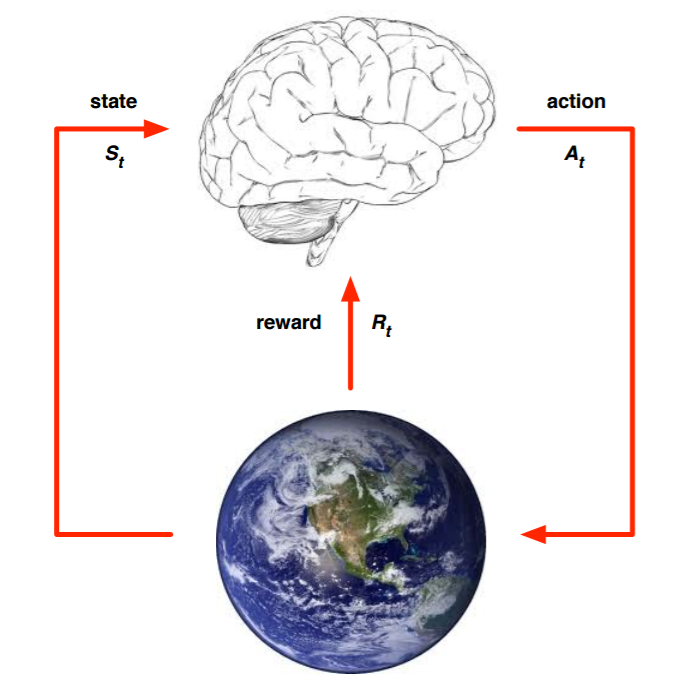
上面的大脑代表我们的算法执行个体，我们可以操作个体来做决策，即选择一个合适的动作（Action）A_tAt。下面的地球代表我们要研究的环境,它有自己的状态模型，我们选择了动作A_tAt后，环境的状态(State)会变，我们会发现环境状态已经变为S_t+1St+1, 同时我们得到了我们采取动作 A_tAt的延时奖励(Reward) R_{t+1Rt+1Tt+1fff}。然后个体可以继续选择下一个合适的动作，然后环境的状态又会变，又有新的奖励值。。。这就是强化学习的思路。

3. 强化学习的简单实例

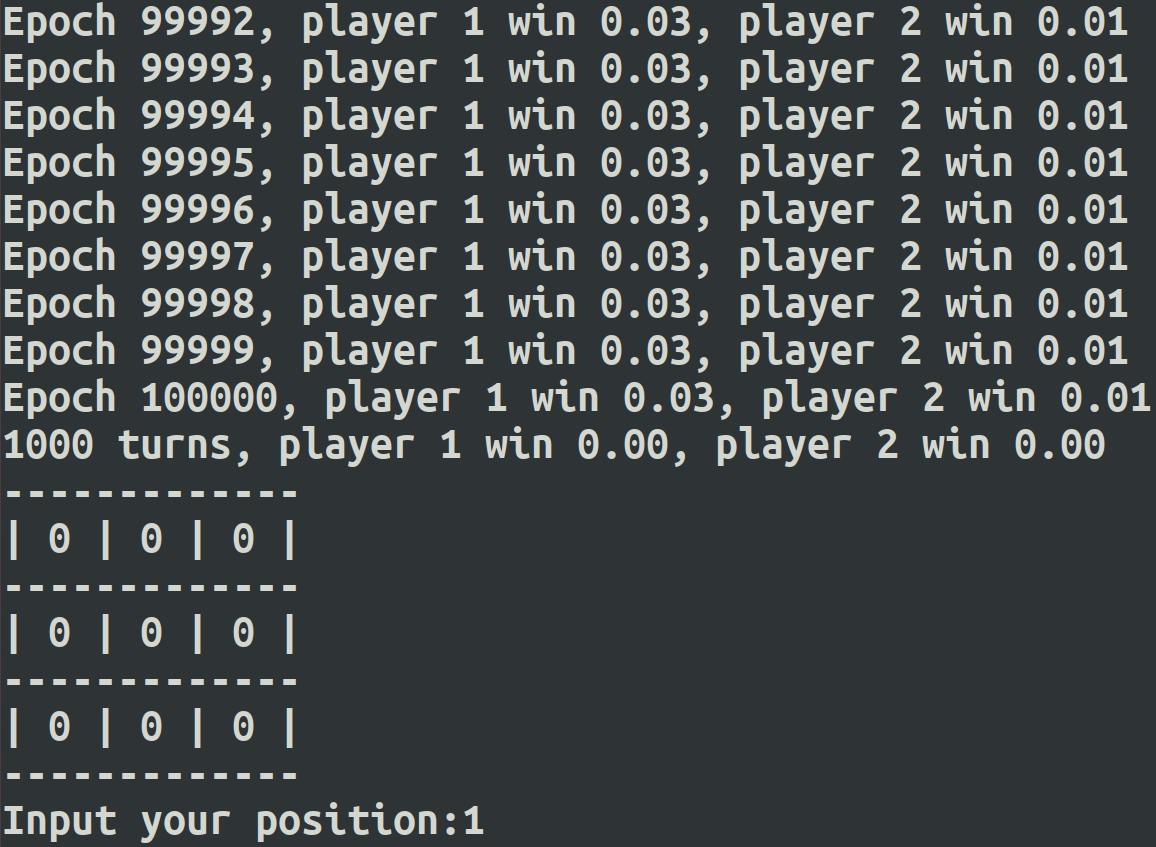
这里给出一个简单的强化学习例子Tic-Tac-Toe。这是一个简单的游戏，在一个3x3的九宫格里，两个人轮流下，直到有个人的棋子满足三个一横一竖或者一斜，赢得比赛游戏结束，或者九宫格填满也没有人赢，则和棋。

这个例子的完整代码在我的github。例子只有一个文件，很简单，代码首先会用两个电脑选手训练模型，然后可以让人和机器对战。当然，由于这个模型很简单，所以只要你不乱走，最后的结果都是和棋，当然想赢电脑也是不可能的。

我们重点看看这个例子的模型，理解上面第二节的部分。如何训练强化学习模型可以先不管。代码部分大家可以自己去看，只有300多行。

 

# give reward to two players
    def giveReward(self):
        if self.currentState.winner == self.p1Symbol:
            self.p1.feedReward(1)
            self.p2.feedReward(0)
        elif self.currentState.winner == self.p2Symbol:
            self.p1.feedReward(0)
            self.p2.feedReward(1)
        else:
            self.p1.feedReward(0.1)
            self.p2.feedReward(0.5)

 

# determine next action
    def takeAction(self):
        state = self.states[-1]
        nextStates = []
        nextPositions = []
        for i in range(BOARD_ROWS):
            for j in range(BOARD_COLS):
                if state.data[i, j] == 0:
                    nextPositions.append([i, j])
                    nextStates.append(state.nextState(i, j, self.symbol).getHash())
        if np.random.binomial(1, self.exploreRate):
            np.random.shuffle(nextPositions)
            # Not sure if truncating is the best way to deal with exploratory step
            # Maybe it's better to only skip this step rather than forget all the history
            self.states = []
            action = nextPositions[0]
            action.append(self.symbol)
            return action

        values = []
        for hash, pos in zip(nextStates, nextPositions):
            values.append((self.estimations[hash], pos))
        np.random.shuffle(values)
        values.sort(key=lambda x: x[0], reverse=True)
        action = values[0][1]
        action.append(self.symbol)
        return action

# update estimation according to reward
    def feedReward(self, reward):
        if len(self.states) == 0:
            return
        self.states = [state.getHash() for state in self.states]
        target = reward
        for latestState in reversed(self.states):
            value = self.estimations[latestState] + self.stepSize * (target - self.estimations[latestState])
            self.estimations[latestState] = value
            target = value
        self.states = []

　　　　第七个是环境的状态转化模型, 这里由于每一个动作后，环境的下一个模型状态是确定的，也就是九宫格的每个格子是否有某个选手的棋子是确定的，因此转化的概率都是1，不存在某个动作后会以一定的概率到某几个新状态，比较简单。

　　　　从这个例子，相信大家对于强化学习的建模会有一个初步的认识了。　　　　　　　　

　　　　以上就是强化学习的模型基础，下一篇会讨论马尔科夫决策过程。

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）

--------------------------------------------------------------------------------------------------------------------------------

#######################################################################
# Copyright (C)                                                       #
# 2016 - 2018 Shangtong Zhang(zhangshangtong.cpp@gmail.com)           #
# 2016 Jan Hakenberg(jan.hakenberg@gmail.com)                         #
# 2016 Tian Jun(tianjun.cpp@gmail.com)                                #
# 2016 Kenta Shimada(hyperkentakun@gmail.com)                         #
# Permission given to modify the code as long as you keep this        #
# declaration at the top                                              #
#######################################################################
##https://www.cnblogs.com/pinard/p/9385570.html ##
## 强化学习（一）模型基础 ##

import numpy as np
import pickle

BOARD_ROWS = 3
BOARD_COLS = 3
BOARD_SIZE = BOARD_ROWS * BOARD_COLS

class State:
    def __init__(self):
        # the board is represented by an n * n array,
        # 1 represents a chessman of the player who moves first,
        # -1 represents a chessman of another player
        # 0 represents an empty position
        self.data = np.zeros((BOARD_ROWS, BOARD_COLS))
        self.winner = None
        self.hash_val = None
        self.end = None

    # compute the hash value for one state, it's unique
    def hash(self):
        if self.hash_val is None:
            self.hash_val = 0
            for i in self.data.reshape(BOARD_ROWS * BOARD_COLS):
                if i == -1:
                    i = 2
                self.hash_val = self.hash_val * 3 + i
        return int(self.hash_val)

    # check whether a player has won the game, or it's a tie
    def is_end(self):
        if self.end is not None:
            return self.end
        results = []
        # check row
        for i in range(0, BOARD_ROWS):
            results.append(np.sum(self.data[i, :]))
        # check columns
        for i in range(0, BOARD_COLS):
            results.append(np.sum(self.data[:, i]))

        # check diagonals
        results.append(0)
        for i in range(0, BOARD_ROWS):
            results[-1] += self.data[i, i]
        results.append(0)
        for i in range(0, BOARD_ROWS):
            results[-1] += self.data[i, BOARD_ROWS - 1 - i]

        for result in results:
            if result == 3:
                self.winner = 1
                self.end = True
                return self.end
            if result == -3:
                self.winner = -1
                self.end = True
                return self.end

        # whether it's a tie
        sum = np.sum(np.abs(self.data))
        if sum == BOARD_ROWS * BOARD_COLS:
            self.winner = 0
            self.end = True
            return self.end

        # game is still going on
        self.end = False
        return self.end

    # @symbol: 1 or -1
    # put chessman symbol in position (i, j)
    def next_state(self, i, j, symbol):
        new_state = State()
        new_state.data = np.copy(self.data)
        new_state.data[i, j] = symbol
        return new_state

    # print the board
    def print(self):
        for i in range(0, BOARD_ROWS):
            print('-------------')
            out = '| '
            for j in range(0, BOARD_COLS):
                if self.data[i, j] == 1:
                    token = '*'
                if self.data[i, j] == 0:
                    token = '0'
                if self.data[i, j] == -1:
                    token = 'x'
                out += token + ' | '
            print(out)
        print('-------------')

def get_all_states_impl(current_state, current_symbol, all_states):
    for i in range(0, BOARD_ROWS):
        for j in range(0, BOARD_COLS):
            if current_state.data[i][j] == 0:
                newState = current_state.next_state(i, j, current_symbol)
                newHash = newState.hash()
                if newHash not in all_states.keys():
                    isEnd = newState.is_end()
                    all_states[newHash] = (newState, isEnd)
                    if not isEnd:
                        get_all_states_impl(newState, -current_symbol, all_states)

def get_all_states():
    current_symbol = 1
    current_state = State()
    all_states = dict()
    all_states[current_state.hash()] = (current_state, current_state.is_end())
    get_all_states_impl(current_state, current_symbol, all_states)
    return all_states

# all possible board configurations
all_states = get_all_states()

class Judger:
    # @player1: the player who will move first, its chessman will be 1
    # @player2: another player with a chessman -1
    # @feedback: if True, both players will receive rewards when game is end
    def __init__(self, player1, player2):
        self.p1 = player1
        self.p2 = player2
        self.current_player = None
        self.p1_symbol = 1
        self.p2_symbol = -1
        self.p1.set_symbol(self.p1_symbol)
        self.p2.set_symbol(self.p2_symbol)
        self.current_state = State()

    def reset(self):
        self.p1.reset()
        self.p2.reset()

    def alternate(self):
        while True:
            yield self.p1
            yield self.p2

    # @print: if True, print each board during the game
    def play(self, print=False):
        alternator = self.alternate()
        self.reset()
        current_state = State()
        self.p1.set_state(current_state)
        self.p2.set_state(current_state)
        while True:
            player = next(alternator)
            if print:
                current_state.print()
            [i, j, symbol] = player.act()
            next_state_hash = current_state.next_state(i, j, symbol).hash()
            current_state, is_end = all_states[next_state_hash]
            self.p1.set_state(current_state)
            self.p2.set_state(current_state)
            if is_end:
                if print:
                    current_state.print()
                return current_state.winner

# AI player
class Player:
    # @step_size: the step size to update estimations
    # @epsilon: the probability to explore
    def __init__(self, step_size=0.1, epsilon=0.1):
        self.estimations = dict()
        self.step_size = step_size
        self.epsilon = epsilon
        self.states = []
        self.greedy = []

    def reset(self):
        self.states = []
        self.greedy = []

    def set_state(self, state):
        self.states.append(state)
        self.greedy.append(True)

    def set_symbol(self, symbol):
        self.symbol = symbol
        for hash_val in all_states.keys():
            (state, is_end) = all_states[hash_val]
            if is_end:
                if state.winner == self.symbol:
                    self.estimations[hash_val] = 1.0
                elif state.winner == 0:
                    # we need to distinguish between a tie and a lose
                    self.estimations[hash_val] = 0.5
                else:
                    self.estimations[hash_val] = 0
            else:
                self.estimations[hash_val] = 0.5

    # update value estimation
    def backup(self):
        # for debug
        # print('player trajectory')
        # for state in self.states:
        #     state.print()

        self.states = [state.hash() for state in self.states]

        for i in reversed(range(len(self.states) - 1)):
            state = self.states[i]
            td_error = self.greedy[i] * (self.estimations[self.states[i + 1]] - self.estimations[state])
            self.estimations[state] += self.step_size * td_error

    # choose an action based on the state
    def act(self):
        state = self.states[-1]
        next_states = []
        next_positions = []
        for i in range(BOARD_ROWS):
            for j in range(BOARD_COLS):
                if state.data[i, j] == 0:
                    next_positions.append([i, j])
                    next_states.append(state.next_state(i, j, self.symbol).hash())

        if np.random.rand() < self.epsilon:
            action = next_positions[np.random.randint(len(next_positions))]
            action.append(self.symbol)
            self.greedy[-1] = False
            return action

        values = []
        for hash, pos in zip(next_states, next_positions):
            values.append((self.estimations[hash], pos))
        np.random.shuffle(values)
        values.sort(key=lambda x: x[0], reverse=True)
        action = values[0][1]
        action.append(self.symbol)
        return action

    def save_policy(self):
        with open('policy_%s.bin' % ('first' if self.symbol == 1 else 'second'), 'wb') as f:
            pickle.dump(self.estimations, f)

    def load_policy(self):
        with open('policy_%s.bin' % ('first' if self.symbol == 1 else 'second'), 'rb') as f:
            self.estimations = pickle.load(f)

# human interface
# input a number to put a chessman
# | q | w | e |
# | a | s | d |
# | z | x | c |
class HumanPlayer:
    def __init__(self, **kwargs):
        self.symbol = None
        self.keys = ['q', 'w', 'e', 'a', 's', 'd', 'z', 'x', 'c']
        self.state = None
        return

    def reset(self):
        return

    def set_state(self, state):
        self.state = state

    def set_symbol(self, symbol):
        self.symbol = symbol
        return

    def backup(self, _):
        return

    def act(self):
        self.state.print()
        key = input("Input your position:")
        data = self.keys.index(key)
        i = data // int(BOARD_COLS)
        j = data % BOARD_COLS
        return (i, j, self.symbol)

def train(epochs):
    player1 = Player(epsilon=0.01)
    player2 = Player(epsilon=0.01)
    judger = Judger(player1, player2)
    player1_win = 0.0
    player2_win = 0.0
    for i in range(1, epochs + 1):
        winner = judger.play(print=False)
        if winner == 1:
            player1_win += 1
        if winner == -1:
            player2_win += 1
        print('Epoch %d, player 1 win %.02f, player 2 win %.02f' % (i, player1_win / i, player2_win / i))
        player1.backup()
        player2.backup()
        judger.reset()
    player1.save_policy()
    player2.save_policy()

def compete(turns):
    player1 = Player(epsilon=0)
    player2 = Player(epsilon=0)
    judger = Judger(player1, player2)
    player1.load_policy()
    player2.load_policy()
    player1_win = 0.0
    player2_win = 0.0
    for i in range(0, turns):
        winner = judger.play()
        if winner == 1:
            player1_win += 1
        if winner == -1:
            player2_win += 1
        judger.reset()
    print('%d turns, player 1 win %.02f, player 2 win %.02f' % (turns, player1_win / turns, player2_win / turns))

# The game is a zero sum game. If both players are playing with an optimal strategy, every game will end in a tie.
# So we test whether the AI can guarantee at least a tie if it goes second.
def play():
    while True:
        player1 = HumanPlayer()
        player2 = Player(epsilon=0)
        judger = Judger(player1, player2)
        player2.load_policy()
        winner = judger.play()
        if winner == player2.symbol:
            print("You lose!")
        elif winner == player1.symbol:
            print("You win!")
        else:
            print("It is a tie!")


if __name__ == '__main__':
    train(int(1e5))
    compete(int(1e3))
play()