原文地址:
http://gameinstitute.qq.com/article/detail/10043
最近在学A* 算法, 在网上看到了这么一个博客,感觉有些意思,虽然看不太懂,但是感觉这个idea还是很不错的,最主要的是出来没有见过这么个法子来处理问题的,这个 分层A* 算法有种要人眼前一亮的感觉, 但是一细看发现这个算法好像还是有很多不足和缺点,但是不管怎么说这个方法还是很值得借鉴的,于是转载如下:
=======================================================
本来经过优化的Normal A*算法已经足以应付最大1024*1024(单位:阻挡格,每个阻挡格大小为:520mm*520mm)的地图了。然而当策划提出野外地图尺寸将达到4096*4096时,Normal A*算法在长距离寻路时就显得力不从心了。在Normal A*算法代码已经没什么优化空间的前提下,我们开始尝试从算法本身着手做一些优化。在参考了《Near Optimal Hierarchical Path-Finding》中提出的一种层次A*算法后,我们给出了优化的思路:
1)预处理:将地图按N*N大小划分区块,其中N为阻挡格数。找出每个区块与周围四个区块在边界上的互通点,然后在区块内使用Normal A*对找出的点做连通性测试并将结果保存下来;
2)层次A*:如果我们将预处理步骤中的区块作为Normal A*算法中搜索的一个阻挡格,那么4096*4096大小的地图,当N=32时的搜索域将会降到128*128。在客户端执行寻路请求时,寻路线程使用预处理得到的数据,在区块一级做一次A*找出路径经过的区块互通点,再在每个区块内使用Normal A*得到互通点之间的路径,最终得到完整路径。
其中,预处理步骤是离线完成的,可在每次变更地图阻挡时执行。如果预处理步骤中预存了区块内的互通点路径,那么在进行层次A*时便可避免在区块内使用Normal A*。
下面详细阐述一下该优化方案的关键算法。
一、预处理
1.1 区块间互通点查找算法
每个相邻区块(C1和C2)都有一条由公共边,该边两侧的格子组成L1和L2,则互通点集E满足下列条件:
o E ⊂ L1 ∪ L2
o ∀t ∈ L1 ∪ L2 : t ∈ E ⇔ symm(t) ∈ E ,其中symm(t)为对称关系
o E不含不可行走点
对在E中且同边的连续格子取其中点,如下图所示:

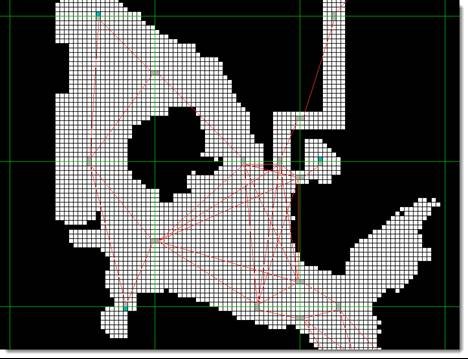
1.2 区块内的路径搜索
一个区块如果与周围区块存在互通点,必定在其内部有一个与之对称的点,通过在区块内执行Normal A*可以得到这些点之间的连通性,该连通关系实际上反映了该区块周围的上下左右区块的连通性。
1.3 预存路径
为了避免客户端在执行层次A*时再耗时去搜索区块内的路径,我们在预处理步骤中将其保存下来。由于A*算法输出的原始结果包含了路径经过的所有格子,为了减少存储消耗,需要对路径进行简化,假设P为A*算法输出的原始路径点集合,O为简化路径点集合:

其中,IsLineConnectivity为直线连通判定,get_back为取集合最尾元素操作,push_back将元素放入集合最尾。
1.4 预处理结果的存储格式
区块尺寸
区块1:
连通点:
UP方向互通点信息:数量,点1索引、点2索引...
DOWN方向互通点信息:...
LEFT方向互通点信息: ...
RIGHT方向互通点信息: …
连通性:
通路数
通路1:两连通点索引,权重,路径长度,路径
通路2:...
区块2:
…
其中,索引均为全局索引。
二、层次A*
2.1 启发式函数
在Normal A*中,启发式函数为F = G + H。在层次A*中,我们沿用这一公式来计算每个搜索节点的权重,只是G与H的计算方法不同了:
- o G:从起点到当前区块边界上互通点路径点的个数
- o H:当前区块到终点所在区块的直线距离
2.2 起点和终点的处理
因为起点与终点是在游戏过程中动态给出的,需要计算它们所处的区块索引,然后先在起点所处区块内以起点到各互通点(区块内部分)做一次Normal A*,将可达互通点对称的点所在的区块放入OpenList并用路径长度作为该区块的G值,如果有多条路径可达同一区块,选取G值最小者。针对终点也做同样处理,但并不放入OpenList,而是将其作为判定是否可达终点所处区块的依据。
三、优化结论及评价
我们对一张1024*1024的地图分别采用32*32、64*64、128*128划分区块,随机产生50个不在阻挡内的起点-终点对,分别使用Normal A*、层次A*、预存路径的层次A*进行测试,结论如下:
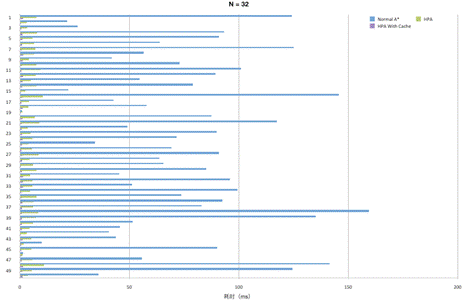
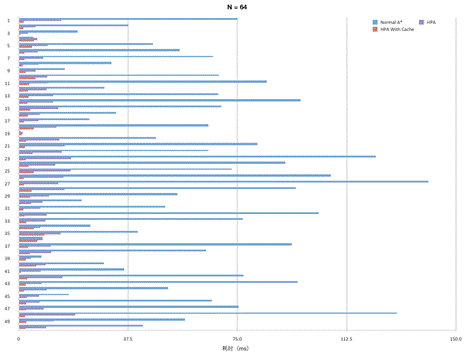
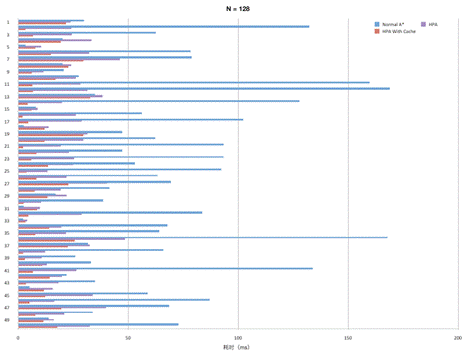
从对比数据可以看出,采用层次A*算法在寻路效率上有很大提升,而且针对不同尺寸的地图N值的选择也需要考虑。此外,该算法也有一定的局限性,主要表现在下面两个方面:
1)不能处理阻挡动态改变的情况;
2)由于区块间的互通点固定,形成的路径可能不是最优的,如下图所示。

由于这两方面的限制,我们主要将其应用在了超过(包括)1024*1024尺寸的主城和野外地图的中远距离寻路中。
参考资料
• A* Pathfinding for Beginners
http://theory.stanford.edu/~amitp/GameProgramming/
• Amit’s A* Pages
http://www.policyalmanac.org/games/aStarTutorial.htm
• Near Optimal Hierarchical Path- Finding
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.72.7041&rep=rep1&type=pdf