题目来源:http://poj.org/problem?id=1062
题目大意:
一个探险家来到一个部落里,想娶部落酋长的女儿,便向酋长求亲。酋长要求10000个金币作为聘礼,同时给出条件:如果探险家能从大祭司处拿到物品A则可以只要8000个金币,如果能要到物品B则可以减至5000个金币。探险家去找大祭司,大祭司也要他用金币来换或者替他获得别的物品来获得优惠,于是探险家又去其它地方找其他人。探险家不需要用多件东西去换取一件东西,因为这样不会得到更低的价格。现在需要你帮助探险家以最少的金币娶到酋长的女儿。需要说明的是,在这个部落里有严格的等级观念,地位差距超过一定限度的两个人之间不能进行直接接触或间接的物品交换。探险家是外来人,所以第一次交易时不用考虑等级约束,但是一旦他开始了第一次交易,他所能接触的人的等级差就不允许超过限制了。(注意,酋长不一定是最高级)。考虑所有的情况为他提供一个最省金币的方案。
为了方便起见,把所有的物品从1开始进行编号,酋长的允诺也看作一个物品,并且编号总是1。每个物品都有对应的价格P,主人的地位等级L,以及一系列的替代品Ti和该替代品所对应的"优惠"Vi。如果两人地位等级差距超过了M,就不能"间接交易"。你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。
输入:输入第一行是两个整数M,N(1 <= N <= 100),依次表示地位等级差距限制和物品的总数。接下来按照编号从小到大依次给出了N个物品的描述。每个物品的描述开头是三个非负整数P、L、X(X < N),依次表示该物品的价格、主人的地位等级和替代品总数。接下来X行每行包括两个整数T和V,分别表示替代品的编号和"优惠价格"。
Sample Input
1 4 10000 3 2 2 8000 3 5000 1000 2 1 4 200 3000 2 1 4 200 50 2 0
Sample Output
5250
本题可转化为求有向图的单源点最短路径问题,然后用经典的Dijkstra算法求解。图的顶点记录物品的原始价格和对应的等级,有向边记录物品替换价格。sample对应的图如下:

若我们求出从酋长对应的顶点出发到其它各顶点的最短路径,再加上该顶点对应的价格,在所得结果中再取最小值,即可得到所需总金币最少的策略。
但到这里还没有结束,因为我们还没有考虑等级限制的问题。最初的想法是在每一次求最短路径的时候都把约束条件加进去,但是这样要考虑的问题比较复杂容易出错,实际上可以用简单的遍历所有可行等级区间的方法来做。由于探险家必须与酋长进行交易才可能达到目的,所以,设酋长的顶级为L1,等级限制为lim,我们可以计算[L1-lim, L1], [L1-lim+1, L1+1]...,[L1, L1+lim]这些可行的区间限制下的解,然后取最小即可。
好了,以上解释了如何把问题转化到单源点最短路径问题上来,接下来讨论该问题的解法:Dijkstra算法。
Dijkstra是一种贪心算法,算法大致流程:每个顶点到源点的路程初始化为其到源点的最短路径,每次把找到的离源点最近的顶点加入已确定最短路径长度的点集中,再从该点沿连边向外扩展,更新各未确定最短路径的顶点到源点的距离,再进行下一次循环直到所有的顶点都加入“已确定的”集合。
维基上给出的伪代码:
1 function Dijkstra(G, w, s) 2 for each vertex v in V[G] // 初始化 3 d[v] : = infinity 4 previous[v] : = undefined 5 d[s] : = 0 6 S : = empty set 7 Q : = set of all vertices 8 while Q is not an empty set // Dijkstra演算法主體 9 u : = Extract_Min(Q) 10 S : = S union { u } 11 for each edge(u, v) outgoing from u 12 if d[v] > d[u] + w(u, v) // 拓展边(u,v) 13 d[v] : = d[u] + w(u, v) 14 previous[v] : = u
运行过程示意动图如下:
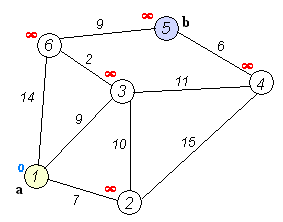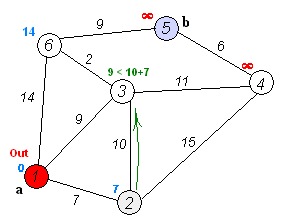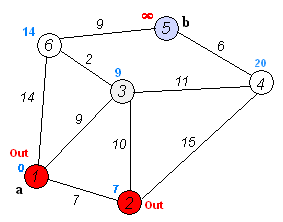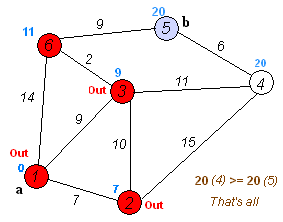
以下是基于上面算法的本题实现:

1 //////////////////////////////////////////////////////////////// 2 // POJ1062 The expensive betrothal presents 3 // Memory: 256K Time: 16MS 4 // Language: C++ Result : Accepted 5 //////////////////////////////////////////////////////////////// 6 7 #include <iostream> 8 #include <algorithm> 9 10 using namespace std; 11 struct Item { 12 int price, level, v; 13 bool confirmed, flag; 14 }; 15 16 int graph[101][101]; 17 Item items[101]; 18 int item_num, level_lim, min_level, max_level; 19 20 int main(void) { 21 cin >> level_lim >> item_num; 22 23 //依据输入构造图 24 memset(graph, -1, sizeof(graph)); 25 for (int i = 1; i <= item_num; ++i) { 26 cin >> items[i].price >> items[i].level >> items[i].v; 27 for (int j = 0; j < items[i].v; ++j) { 28 int item_id, price; 29 cin >> item_id >> price; 30 graph[i][item_id] = price; 31 } 32 items[i].v = 10000; //初始化以该物品为兑换终点的路径总共需要的金钱 33 } 34 35 items[0].v = 10000; 36 //加限制的Dijkstra算法求单源点最短路径 37 int min_v = 10000; 38 //遍历各可行区间 39 for (min_level = items[1].level - level_lim; min_level <= items[1].level; ++min_level) { 40 max_level = min_level + level_lim; 41 items[1].v = 0; 42 items[1].confirmed = true; 43 for (int i = 2; i <= item_num; ++i) { 44 if (items[i].level >= min_level && items[i].level <= max_level) { 45 items[i].flag = true; 46 items[i].v = graph[1][i] != -1 ? graph[1][i] : 10000; 47 items[i].confirmed = false; 48 } else { 49 items[i].flag = false; 50 } 51 } 52 53 int last_confirmed = 1; 54 for (int i = 2; i <= item_num; ++i) { 55 int min_id = 0; 56 for (int j = 2; j <= item_num; ++j) { 57 if (!items[j].confirmed) { 58 if (items[j].flag == true //等级符合要求 59 && graph[last_confirmed][j] != -1 //与刚才确认最短路径的顶点相连 60 && items[last_confirmed].v + graph[last_confirmed][j] < items[j].v) { //该路径短于之前的最短路径 61 items[j].v = items[last_confirmed].v + graph[last_confirmed][j]; 62 } 63 if (items[j].v < items[min_id].v) { 64 min_id = j; 65 } 66 } 67 } 68 items[min_id].confirmed = true; 69 last_confirmed = min_id; 70 } 71 72 //求价格最小值 73 for (int i = 1; i <= item_num; ++i) { 74 items[i].v += items[i].price; 75 min_v = min(items[i].v, min_v); 76 } 77 } 78 cout << min_v << endl; 79 return 0; 80 }
用堆理论上可以对算法进行优化,但是大概因为本题的数据不大,加了堆优化的没有明显的速度提升。

1 //////////////////////////////////////////////////////////////// 2 // POJ1062 The expensive betrothal presents 3 // Memory: 256K Time: 16MS 4 // Language: C++ Result : Accepted 5 //////////////////////////////////////////////////////////////// 6 7 #include <iostream> 8 #include <algorithm> 9 10 using namespace std; 11 struct Item { 12 int price, level, v, gid; 13 }; 14 15 int graph[101][101]; 16 Item heap[101]; 17 int item_num, heap_size, level_lim, min_level, max_level; 18 19 void heapify(int i) { 20 if (i > heap_size / 2) { 21 return; 22 } 23 int min_i = i; 24 if (2 * i <= heap_size && heap[i].v > heap[2 * i].v) { 25 min_i = 2 * i; 26 } 27 if (2 * i + 1 <= heap_size && heap[min_i].v > heap[2 * i + 1].v) { 28 min_i = 2 * i + 1; 29 } 30 if (min_i != i) { 31 Item t = heap[i]; 32 heap[i] = heap[min_i]; 33 heap[min_i] = t; 34 heapify(min_i); 35 } 36 } 37 38 void Build_Heap(void) { 39 heap_size = item_num - 1; 40 heap[0].v = 0; 41 for (int i = 1; i <= heap_size; ++i) { 42 if (graph[0][heap[i].gid] != -1 && heap[i].level >= min_level 43 && heap[i].level <= max_level) { 44 heap[i].v = graph[0][heap[i].gid]; 45 } else { 46 heap[i].v = 20000; 47 } 48 } 49 for (int i = heap_size / 2; i > 0; --i) { 50 heapify(i); 51 } 52 } 53 54 int Extract_Min(void) { 55 Item ret = heap[1]; 56 heap[1] = heap[heap_size]; 57 heap[heap_size] = ret; 58 --heap_size; 59 heapify(1); 60 return heap_size + 1; 61 } 62 63 void Decrease_Key(int i, int k) { 64 heap[i].v = k; 65 while (i > 1 && heap[i / 2].v > heap[i].v) { 66 Item t = heap[i]; 67 heap[i] = heap[i / 2]; 68 heap[i / 2] = t; 69 i = i / 2; 70 } 71 } 72 73 int main(void) { 74 cin >> level_lim >> item_num; 75 76 //依据输入构造图 77 memset(graph, -1, sizeof(graph)); 78 for (int i = 0; i < item_num; ++i) { 79 cin >> heap[i].price >> heap[i].level >> heap[i].v; 80 heap[i].gid = i; 81 for (int j = 0; j < heap[i].v; ++j) { 82 int item_id, price; 83 cin >> item_id >> price; 84 graph[i][item_id - 1] = price; 85 } 86 } 87 88 //加限制的Dijkstra算法求单源点最短路径(最小堆优化实现) 89 int king_level = heap[0].level; 90 //heap[0].confirmed = true; 91 int min_v = 10000; 92 //遍历各可行区间 93 for (min_level = king_level - level_lim; min_level <= king_level; ++min_level) { 94 max_level = min_level + level_lim; 95 heap[0].v = 0; 96 Build_Heap(); 97 while (heap_size > 0) { 98 int r = Extract_Min(); 99 for (int i = 1; i <= heap_size; ++i) { 100 int lastv = heap[r].gid; 101 int new_v = graph[lastv][heap[i].gid] + heap[r].v; 102 if (graph[lastv][heap[i].gid] != -1 && heap[i].level >= min_level 103 && heap[i].level <= max_level && new_v < heap[i].v) { 104 Decrease_Key(i, new_v); 105 } 106 } 107 } 108 //求价格最小值 109 for (int i = 0; i < item_num; ++i) { 110 heap[i].v += heap[i].price; 111 min_v = min(heap[i].v, min_v); 112 } 113 } 114 cout << min_v << endl; 115 return 0; 116 }
附上Discuss里的几组测试数据:

测试数据1: 1 4 10000 3 2 2 8000 3 5000 1000 2 1 4 200 3000 2 1 4 200 50 2 0 5250 测试数据2: 1 5 10000 3 4 2 3000 3 2000 4 2000 5 9000 8000 2 3 3 5000 4 2000 5 7000 5000 1 0 2000 4 1 5 1900 50 1 0 4000 测试数据3: 3 8 10000 3 6 2 3000 3 2000 4 2000 5 9000 7 1000 8 5008 8000 2 3 3 5000 4 2000 5 7000 5000 1 1 6 1000 2000 4 1 5 1900 50 1 0 5000 1 1 7 4007 2000 4 1 5 1900 80 3 0 2950 测试数据4: 1 10 1324 0 0 1234 0 0 255 0 0 67 0 0 56 0 0 2134 0 0 456 0 0 2345 0 0 67 0 0 6436 0 0 1324 测试数据5: 1 4 10000 3 2 2 1 3 3 1000 2 2 4 1 3 1 1000 3 1 4 2 100 4 0 105 测试数据6: 3 5 10000 3 4 2 3000 3 2000 4 2000 5 9000 8000 2 3 3 5000 4 2000 5 7000 5000 1 0 2000 4 1 5 1900 50 1 0 3950 测试数据7: 0 5 10000 3 4 2 3000 3 2000 4 2000 5 9000 8000 2 3 3 5000 4 2000 5 7000 5000 4 0 2000 3 1 5 1900 50 2 0 4000
