POJ1039 Pipe

题目来源：http://poj.org/problem?id=1039

题目大意：

　　有一条宽度为1(指的是上下管壁纵坐标之差，不是管道真实的宽度)的折线形管道，管道壁不透光不反光，求从管道一头射入一束光线，光线在管道内沿直线传播最远能传播多远(横坐标能到达的最大值)。如图所示：

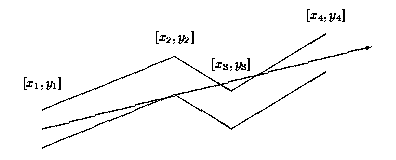
输入：每个测试用例一个数据块，第一个整数为折点数（2到20之间），接下来每行一个折点坐标(即上图中的一个点[x,y]，x互不相等，按增序排列)，表示管道的上边界折点，对应的下边界折点为[x,y-1].折点数位0时表示输入结束。

输出：每次用例输出一行，若光线能穿透整个管道，输出Through all the pipe.否则输出能到达的x值，保留两位小数。

---

Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

---

本题属于计算几何。其实的数学基础只需要于中学解析几何的水准就可以解决了吧。

首先，分析可以发现，能照到最远的x的光线应该是经过一个上管壁折点和一个下管壁折点的。当光线可以穿透全管时，总可以把光线平移或旋转至经过一个上管壁折点和一个下管壁折点，光线不能穿透全管时，若某光线不满足上面的条件，通过旋转和平移，一定能够使得x继续向右延伸。

所以只需要遍历由一个上壁折点和一个下壁折点确定的直线，查找x可到达的最大值即可。（如果只有一段管道，显然可以穿过，不再计算。）

求一条直线能到达的最大x值使用的方法是：

首先，判断这条直线与管道入口截面的交点是否在入口范围内，如不在，则说明从入口处不可能发射出这条直线，淘汰之。

否则，从分别考虑每一段管道，光线通过的情况。接下来实际上就是模拟了。

若直线与这段管道右截面的交点在出口范围内，则这段管道可以被穿透，进入下一段管道；否则，直线一定在管道内与管道壁相交，交点的x值即该条直线能到达的最大x值。

若直线斜率k大于管道斜率kb，则交点在上管壁，求直线与上管壁交点的横坐标。否则，求直线与下管壁交点的横坐标。平行的情况以及被前面的特例处理过了，这里不需再考虑。

由于这道题里的折点x坐标是递增的，各不相等，所以不会出现斜率不存在的情况，所以用直线的斜截式表示比较方便。

因为用的是double类型，精度问题需要注意一下，小菜在这个问题上被折磨的死去活来的..T_T.开始自己写的一个方法，思想和这个是一样的，只是在相交判断等细节上稍有不同的处理，就怎么也过不了，后来选择了浮点乘除运算稍微少一点的方法，开始把代码里的eps设为1e-3提交WA，改为1e-4才通过，果然计算几何什么的好多细节的东西要注意啊。

////////////////////////////////////////////////////////////////////////
//        POJ1039 Pipe
//        Memory: 168K        Time: 32MS
//        Language: C++        Result: Accepted
//////////////////////////////////////////////////////////////////////////

#include <cstdio>
#include<cmath>

using namespace std;

int cnt;
double node[20][2];
double k;    //斜率
double b;    //截距
double xmax;

//精度控制
inline int cmp(const double & p) {
    if (fabs(p) < 1e-4)
        return 0;
    return p > 0 ? 1 : -1;
}

//由两点确定直线方程
void makeLine(double x1, double y1, double x2, double y2) {
    double a0 = y2 - y1;
    double b0 = x1 - x2;
    double c0 = x2 * y1 - y2 * x1;
    k = -1 * a0 / b0;
    b = -1 * c0 / b0;
}

//求直线与管壁交点的x值
double intersect(double x1, double y1, double x2, double y2) {
    return (x1 * (y2 - y1) + (x2 - x1) * (b - y1)) / (y2 - y1 - k * (x2 - x1));
}

double check() {
    double y0 = k * node[0][0] + b;
    //不可能从入口发出这道光线
    if (cmp(y0 - node[0][1]) > 0 || cmp(y0 - node[0][1] + 1) < 0) {
        return node[0][0];
    }
    double ans = node[cnt - 1][0];
    for (int i = 0; i < cnt - 1; ++i) {
        double y1 = k * node[i + 1][0] + b;
        //可以穿过这段管道
        if (cmp(y1- node[i + 1][1] + 1) >= 0 && cmp(y1 - node[i + 1][1]) <= 0) {
            continue;
        }
        //管道斜率
        double kb = (node[i + 1][1] - node[i][1]) / (node[i + 1][0] - node[i][0]);
        int dk = cmp(k - kb);
        if (dk > 0) {
            //与上管壁交点
            return intersect(node[i][0], node[i][1], node[i + 1][0], node[i + 1][1]);
        } else {
            //与下管壁交点
            return intersect(node[i][0], node[i][1] - 1, node[i + 1][0], node[i + 1][1] - 1);
        }
    }
    return ans;
}

int main(void) {
    while (true) {
        scanf("%d", &cnt);
        if (cnt == 0) {
            break;
        }
        for (int i = 0; i < cnt; ++i) {
            scanf("%lf%lf", &node[i][0], &node[i][1]);
        }
        if (cnt == 2) {
            //只有一段管道，一定可以穿过，不用再计算
            printf("Through all the pipe.
");
            continue;
        }
        xmax = node[1][0];
        for (int i = 0; i < cnt - 1; ++i) {
            for (int j = i + 1; j < cnt; ++j) {
                //第i个上顶点与第j个下顶点组成直线
                makeLine(node[i][0], node[i][1], node[j][0], node[j][1] - 1);
                double now = check();
                if (now > xmax) xmax = now;
                //第i个下顶点与第j个上顶点组成直线
                makeLine(node[i][0], node[i][1] - 1, node[j][0], node[j][1]);
                now = check();
                if (now > xmax) xmax = now;
            }
        }
        if (cmp(xmax - node[cnt - 1][0]) == 0) {
            printf("Through all the pipe.
");
        } else {
            printf("%.2lf
", xmax);
        }
    }
    return 0;
}