1、什么是快速排序算法？
快速排序是由东尼·霍尔所发展的一种排序算法，犹如他的名字一样，速度快，效率高，也是实际
中最常用的一种算法，被称为20实际对世界影响最大的算法之一。
基本思想:
1): 从序列中挑出一个元素作为"基准"元素，一般是该序列的第一个元素或者是最后一个元素。
2): 把序列分成2个部分，其数值大于"基准"元素的元素放在"基准"元素的左边，否在放在"基准"元
素的右边，此时"基准"元素所在的位置就是正确的排序位置，这个过程被称为 partition（分区）。
3): 递归将"基准"元素左边的序列和"基准"元素右边的序列进行partition操作。
2、算法的演示
这个就是待排序的数组序列，第一个元素作为"基准"元素
给"基准"元素找到合适的位置，将比"基准"元素小的元素放在其左边，否则放在其右边
至此这个序列就成了这样了，这个过程成为partition
下面来看看partition的具体实现过程:
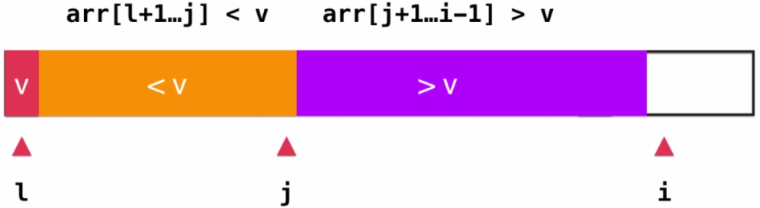
将"基准"元素用v表示，使用i作为遍历序列的索引值，j的位置
表示>v部分和<v部分的分界位置（也就是最后一个小于v的元
素所在位置）。
如果此时i指向的元素大于v，这个好处理，直接将i++即可，
也就表示大于v的元素多了一个
如果此时i指向的元素小于v，那么需要将i指向的元素与大于
v序列的第一个元素交换位置，即swap(arr[i], arr[j+1])，
然后再将i++，再将j++即可，表示小于v的元素多了一个。
如下图所示
进行swap(arr[i], arr[j+1])
j++
i++
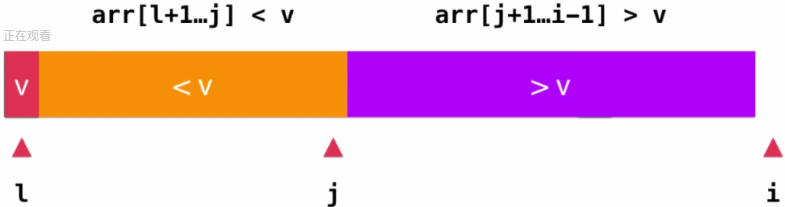由此可知，当遍历完成之后，就会出现这样的效果，然后我
们只需将元素v与j指向的元素交换位置即可
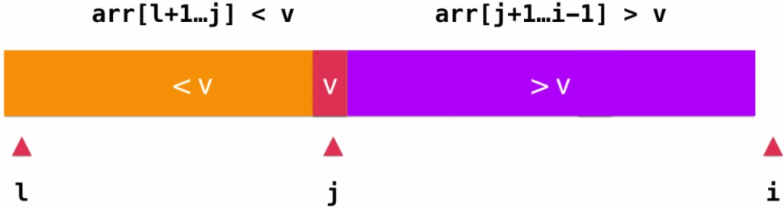此时就出现了小于"基准"元素的元素在其左边，大于"基准"
元素的元素在其右边的分布情况
3、算法实现的动画效果
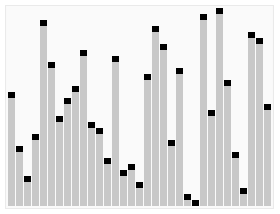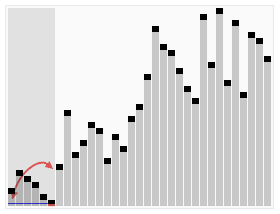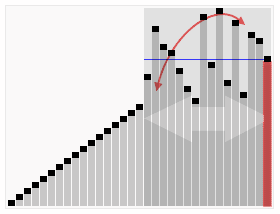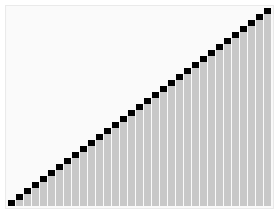
4、算法的实现（基于C++）
1 /*********************************** 随机化快速排序算法实现 ****************************************/ 2 // 对arr[left....right]进行partition操作 3 // 返回p，使得arr[left, p-1] < arr[p]，arr[p+1, right] > arr[p] 4 template<typename T> 5 int __partition (T arr[], int left, int right) 6 { 7 T v = arr[left]; // 将第一个元素作为"基准"元素 8 int j = left; // 将<v部分的分界点位置j初始化为本序列中的第一个元素位置（也就是<v部分的最后一个元素位置） 9 10 // 将遍历序列的索引值i初始为第二个元素位置 11 for (int i = left + 1; i <= right; i++) { 12 if (arr[i] < v) { // 如果i指向的元素<v，那么将此元素与>v部分的第一个元素交换位置，然后j++，表示<v的元素又多了一个 13 j++; 14 std::swap(arr[j], arr[i]); // 这里采用了另一种那写法，因为j++之后指向的就是>v部分的第一个元素，交换位置之后其实类似于将>v的部分整体往右边移动了一个位置 15 } 16 } 17 18 std::swap(arr[left], arr[j]); // 遍历完成之后只需要将"基准"元素（也就是第一个元素）与当前j指向的位置交换位置即可 19 return j; // 因为"基准"元素并不属于<v的部分，所以交换之后此时j指向的元素就是"基准"元素 20 } 21 22 // 对arr[left...right]范围内数组序列进行快速排序操作 23 template<typename T> 24 void __quickSort (T arr[], int left, int right) 25 { 26 int p = __partition<T>(arr, left, right); // 对arr[left...right]区间元素进行partition操作，找到"基准"元素 27 __quickSort<T>(arr, left, p - 1); // 对基准元素之前的序列递归调用__quickSort函数 28 __quickSort<T>(arr, p + 1, right); // 对基准元素之后的序列递归调用__quickSort函数 29 } 30 31 template<typename T> 32 void quickSort (T arr[], int count) 33 { 34 __quickSort<T>(arr, 0, count - 1); // 调用__quickSort函数进行快速排序 35 } 36 /********************************************************************************************/
5、算法性能测试
与前面的2种归并排序算法相比较
测试数据量100000:
测试数据量1000000:
从上面可以知道，很明显快速排序要比归并排序快，这还是在快速排序没有优化的情况下。不同的
电脑由于配置不一样，可能得到的测试结果是不同的。
6、快速排序算法的优化
(1)第一种优化
在前面的学习过程中已经说到了，那就是对于几乎所有的高级算法都可以使用的一种优化方法，
当递归到元素个数很小时可以使用直接插入排序。
(2)第二种优化（随机化快速排序算法）
我们先来看一个例子，当待排序的数组序列接近为一个有序序列的时候，归并排序和快速排序的性能测试
测试数据量500000:
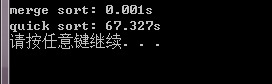
通过上面可以知道，当序列接近为有序状态的时候，快速排序慢得要死，这是为什么呢？请看下面的分析:
对于快速排序，因为我们是将第一个元素作为"基准"元素，但由于序列基本接近为有序，从而导致每一个
"基准"元素的左边没有一个元素，而全部
在他的右边，这样就会导致快速排序算法的高度为n，将退化为O(n^2)级别。
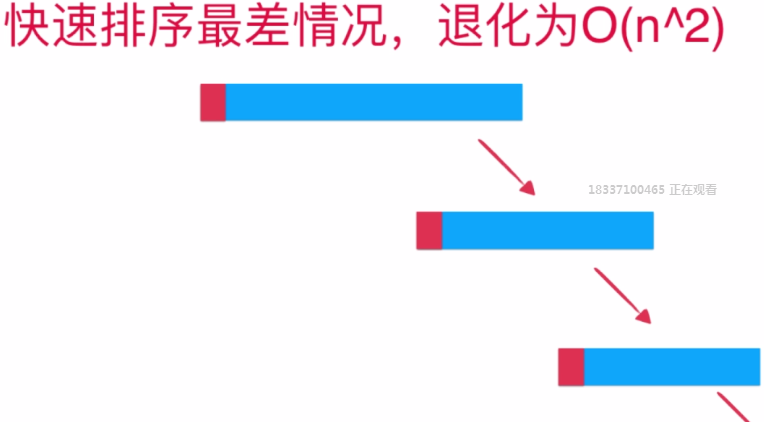
那么这种情况的解决办法就是: 尽可能的别让第一个元素成为"基准"元素，而最好使用中间位置的元素成为
"基准"元素，那如何做到这点呢？
解决办法就是"基准"元素随机产生，而不指定。请看下面的代码:
1 /*********************************** 随机化快速排序算法实现 ****************************************/ 2 // 对arr[left....right]进行partition操作 3 // 返回p，使得arr[left, p-1] < arr[p]，arr[p+1, right] > arr[p] 4 template<typename T> 5 int __partition (T arr[], int left, int right) 6 { 7 std::swap(arr[left], arr[std::rand()%(right-left+1)+left]); // 随机产生"基准"元素所在位置，并与第一个元素交换位置 8 9 T v = arr[left]; // 将第一个元素作为"基准"元素 10 int j = left; // 将<v部分的分界点位置j初始化为本序列中的第一个元素位置（也就是<v部分的最后一个元素位置） 11 12 // 将遍历序列的索引值i初始为第二个元素位置 13 for (int i = left + 1; i <= right; i++) { 14 if (arr[i] < v) { // 如果i指向的元素<v，那么将此元素与>v部分的第一个元素交换位置，然后j++，表示<v的元素又多了一个 15 j++; 16 std::swap(arr[j], arr[i]); // 这里采用了另一种那写法，因为j++之后指向的就是>v部分的第一个元素，交换位置之后其实类似于将>v的部分整体往右边移动了一个位置 17 } 18 } 19 20 std::swap(arr[left], arr[j]); // 遍历完成之后只需要将"基准"元素（也就是第一个元素）与当前j指向的位置交换位置即可 21 return j; // 因为"基准"元素并不属于<v的部分，所以交换之后此时j指向的元素就是"基准"元素 22 } 23 24 // 对arr[left...right]范围内数组序列进行快速排序操作 25 template<typename T> 26 void __quickSort (T arr[], int left, int right) 27 { 28 if (right - left <= 40) { // 对归并到序列中元素个数较小时采用插入排序算法 29 __insertSortMG<T>(arr, left, right); 30 return; 31 } 32 33 int p = __partition<T>(arr, left, right); // 对arr[left...right]区间元素进行partition操作，找到"基准"元素 34 __quickSort<T>(arr, left, p - 1); // 对基准元素之前的序列递归调用__quickSort函数 35 __quickSort<T>(arr, p + 1, right); // 对基准元素之后的序列递归调用__quickSort函数 36 } 37 38 template<typename T> 39 void quickSort (T arr[], int count) 40 { 41 std::srand(std::time(NULL)); // 种下随机种子 42 __quickSort<T>(arr, 0, count - 1); // 调用__quickSort函数进行快速排序 43 } 44 /********************************************************************************************/
这次的改变在于: 在quickSort函数中种下了随机种子，然后在__partition函数中使用rand函数来产生随机的位置，
将此位置的元素作为"基准"元素，从而可以避免使用第一个元素作为"基准"。使用了随机化快速排序之后，虽然在排
序一般的序列时会比之前的快速排序算法要慢，但是之前的快速排序算法对于一个近乎有序的序列时就不行了，而随
机化快速排序就能够很好的解决这样的问题，所以随机化快速排序就能够兼顾这样两种不同的情况，而且还能够快速
的对序列进行排序。来看看与归并排序算法之间的性能比较:
一般序列数据量1000000:
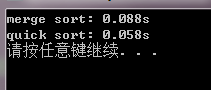
近乎有序的序列数据量1000000:
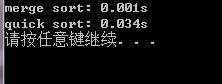
从上面的测试得到的结果可以看出来，对于一般的序列使用随机化快速排序要比归并排序快，而对于近乎有序的序
列明显归并排序要快，这是归并排序的一个优势，之前说过；但是实际中出现近乎有序序列的概率是很低很低的，
所以完全可以认为随机化快速排序在总体上比归并排序快。