B. Count Subrectangles

You are given an array aa of length nn and array bb of length mm both consisting of only integers 00 and 11. Consider a matrix cc of size n×mn×m formed by following rule: ci,j=ai⋅bjci,j=ai⋅bj (i.e. aiai multiplied by bjbj). It's easy to see that cc consists of only zeroes and ones too.

How many subrectangles of size (area) kk consisting only of ones are there in cc?

A subrectangle is an intersection of a consecutive (subsequent) segment of rows and a consecutive (subsequent) segment of columns. I.e. consider four integers x1,x2,y1,y2x1,x2,y1,y2 (1≤x1≤x2≤n1≤x1≤x2≤n, 1≤y1≤y2≤m1≤y1≤y2≤m) a subrectangle c[x1…x2][y1…y2]c[x1…x2][y1…y2] is an intersection of the rows x1,x1+1,x1+2,…,x2x1,x1+1,x1+2,…,x2 and the columns y1,y1+1,y1+2,…,y2y1,y1+1,y1+2,…,y2.

The size (area) of a subrectangle is the total number of cells in it.

Input

The first line contains three integers nn, mm and kk (1≤n,m≤40000,1≤k≤n⋅m1≤n,m≤40000,1≤k≤n⋅m), length of array aa, length of array bb and required size of subrectangles.

The second line contains nn integers a1,a2,…,ana1,a2,…,an (0≤ai≤10≤ai≤1), elements of aa.

The third line contains mm integers b1,b2,…,bmb1,b2,…,bm (0≤bi≤10≤bi≤1), elements of bb.

Output

Output single integer — the number of subrectangles of cc with size (area) kk consisting only of ones.

Examples

input

Copy

3 3 2
1 0 1
1 1 1

output

Copy

4

input

Copy

3 5 4
1 1 1
1 1 1 1 1

output

Copy

14

Note

In first example matrix cc is:

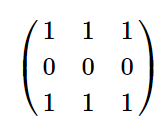
There are 44 subrectangles of size 22 consisting of only ones in it:

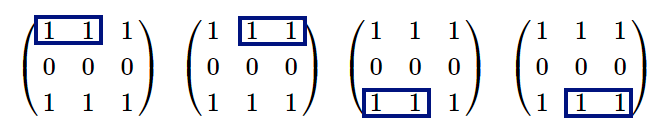
In second example matrix cc is:

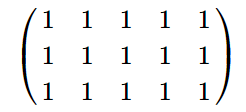
#include <bits/stdc++.h>
#define ll              long long
#define PII             pair<int, int>
#define rep(i,a,b)      for(int  i=a;i<=b;i++)
#define dec(i,a,b)      for(int  i=a;i>=b;i--)
using namespace std;
int dir[4][2] = { { 0,1 } ,{ 0,-1 },{ 1,0 },{ -1,0 } };
const long long INF = 0x7f7f7f7f7f7f7f7f;
const int inf = 0x3f3f3f3f;
const double pi = 3.14159265358979323846;
const int mod = 998244353;
const int N = 1e5+5;
inline ll read()
{
    ll x = 0; bool f = true; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = false; c = getchar(); }
    while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    return f ? x : -x;
}
ll gcd(ll m, ll n)
{
    return n == 0 ? m : gcd(n, m%n);
}
ll lcm(ll m, ll n)
{
    return m*n / gcd(m, n);
}
vector<ll> gao(vector<int> a)
{
    int n=a.size();
    vector<ll> res(n+1);
    int i=0;
    while(i<n)
    {
        if(a[i]==0)
        {
            i++;
            continue;
        }
        int j=i;
        while(j<n&&a[j]==1)
        {
            j++;
        }
        for(int len =1;len<=j-i;len++)
        {
            res[len]+=j-i-len+1;
        }
        i=j;
    }
    return res;
}
int main()
{
    int n,m,k;
    cin>>n>>m>>k;
    vector<int> a(n),b(m);
    for(int i=0;i<n;i++)
        a[i]=read();
    for(int i=0;i<m;i++)
        b[i]=read();
    auto a0=gao(a);
    auto b0=gao(b);
    ll ans=0;
    for(int i=1;i<a0.size();i++)
    {
        if(k%i==0 && k/i<=m)
        {
            ans+=a0[i]*b0[k/i];
        }
    }
    cout<<ans<<endl;
    return 0;
}