题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
解题所需的知识
二叉树的遍历
这个先中后,是根据何时遍历根节点命名的,左的优先级大于后,比如先序就先遍历根结点,再遍历左节点,最后遍历右节点,中序同理,先左中根最后右,后序,先左再右后根。

二叉树的先序遍历
来! 根据上面的的顺序我们来走一遍,先根再左最后右。
首先,显而意见,1是根节点
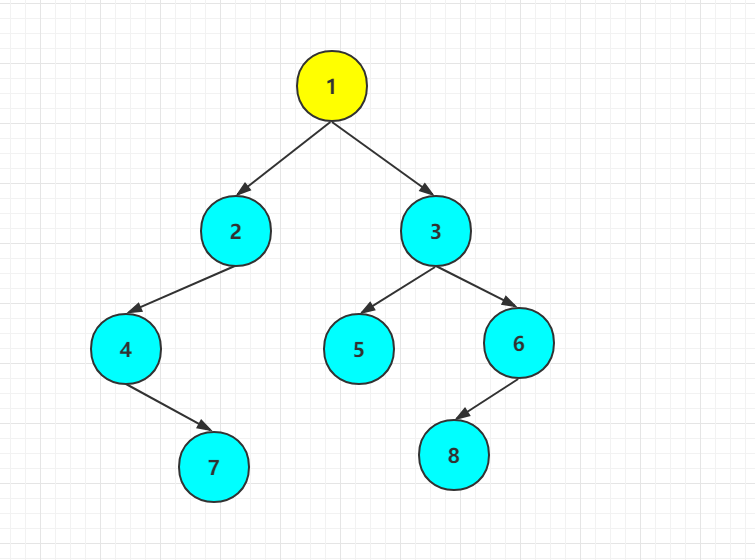
那么现在往左走,发现 2,4,7 也是一棵二叉树,他也是二叉树,我们可不能区别对待,所以理应也满足先序遍历,先根再左最后右。那么2就是这颗小二叉树的根节点啦。

找到了小二叉树的根节点,按照先序再走左,发现4,7也是一棵二叉树,这颗小小二叉树也得满足先序哦,4为根节点,再走左,发现左没了,还记得先序得遍历规则嘛 先根再左后右,左没了那就轮到右啦,所以应该走7了,走完7以后,4,7这棵小小小二叉树算是走完了,走完之后该走2,4,7这颗小二叉树的右节点了,依次类推哦。
先序遍历为 1,2,4,7,3,5,6,8
二叉树的中序遍历
同上 4,7,2,1,5,3,8,6
二叉树的后序遍历
同上 7,4,2,5,8,6,3,1
根据先序,中序构建二叉树
举例 前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
首先,先序先遍历根节点,那么1显然就是最上面的那个根节点,中序是中间遍历根节点,那么显然可以得出如下图

那么继续去前序得数组中找,发现4,7,2最先出现的是2,那显然2是4,7,2的根结点,去中序找,4,7都在2之前,那显然都是2的左子树。

再去先序找,发现4先出现,那么4就是4,7的根节点,去中序找,发现7在4的右边,说明是右子树。

右子树依次类推。。。。。
代码实现
人用迭代,神用递归
我们用递归的思想,首先先序{1,2,4,7,3,5,6,8},中序{4,7,2,1,5,3,8,6},那么我们找到1是根节点:
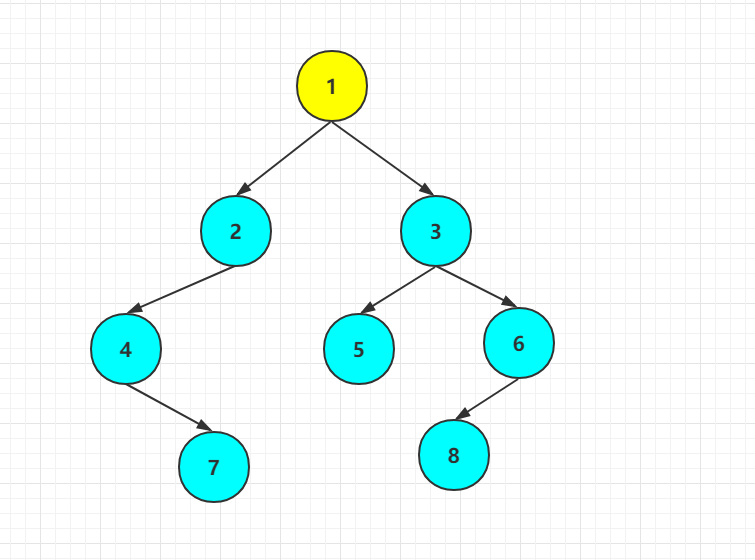
那么现在我们把4,7,2当成一棵二叉树,那么先序从上面知道是{2,4,7} 中序根据上面也知道是{4,7,2},那接下来跟我们找出1是根节点然后分左右是不是一模一样,只不过先序的数组和中序的数组变了
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
//前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
int len = pre.length;
TreeNode root = new TreeNode(pre[0]);
//说明只剩下一个了,表示叶子节点,递归可以退出了
if (pre.length == 1) {
root.left = null;
root.right = null;
return root;
}
//中间值 在{4,7,2,1,5,3,8,6} 这个中间值第一次应该是3
int flag = 0;
for (int i = 0; i < len; i++) {
//在中序中找到
if (pre[0] == in[i]) {
flag = i;
break;
}
}
if (flag > 0) {
//左子树的先序
int[] leftPre = new int[flag];
//左子树的中序
int[] leftIn = new int[flag];
for (int j = 0; j < flag; j++) {
leftPre[j] = pre[j + 1];
}
for (int j = 0; j < flag; j++) {
leftIn[j] = in[j];
}
//左子树递归
root.left = reConstructBinaryTree(leftPre, leftIn);
} else {
root.left = null;
}
if (pre.length - flag - 1 > 0) {
//右子树的先序,长度为 总-根-左子树
int[] rightPre = new int[pre.length - 1 - flag];
//右子树的中序
int[] rightIn = new int[pre.length - 1 - flag];
for (int j = flag + 1; j < len; j++) {
//右子树中序,为什么要j-flag-1呢 因为我的rightIn要从0开始 而j是k+1开始的 ,所以很尴尬,只能用j-flag-1
rightIn[j - flag - 1] = in[j];
rightPre[j - flag - 1] = pre[j];
}
root.right = reConstructBinaryTree(rightPre, rightIn);
} else {
root.right = null;
}
return root;
}
}