1.什么是TSP问题
一个售货员必须访问n个城市,这n个城市是一个完全图,售货员需要恰好访问所有城市的一次,并且回到最终的城市。
城市于城市之间有一个旅行费用,售货员希望旅行费用之和最少。
完全图:完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。
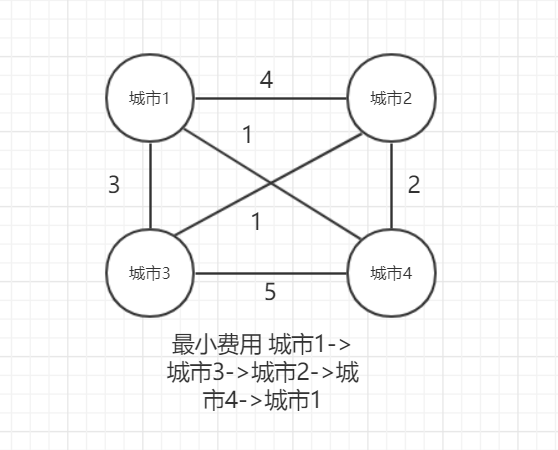
2.TSP问题前提
回朔法:把所有的解列出来,形成一棵树,利用剪枝深度优先进行遍历,遍历的过程记录和寻找最优解。(剪枝就是把一条再深搜下去也不是最优解的分支剪去)。
动态规划:把一个大问题拆分成小问题,把小问题的最优结果通过表保留,在新问题需要用到的时候可以直接获取。
PS:下面的图,文字中出现1,2,3,4分别表示城市1,城市2,城市3,城市4
3.回朔法实现TSP问题
上面提到回朔法就是把所有的解列出来,形成一棵树,上面的例子形成的树如下:我们假设城市1为起点
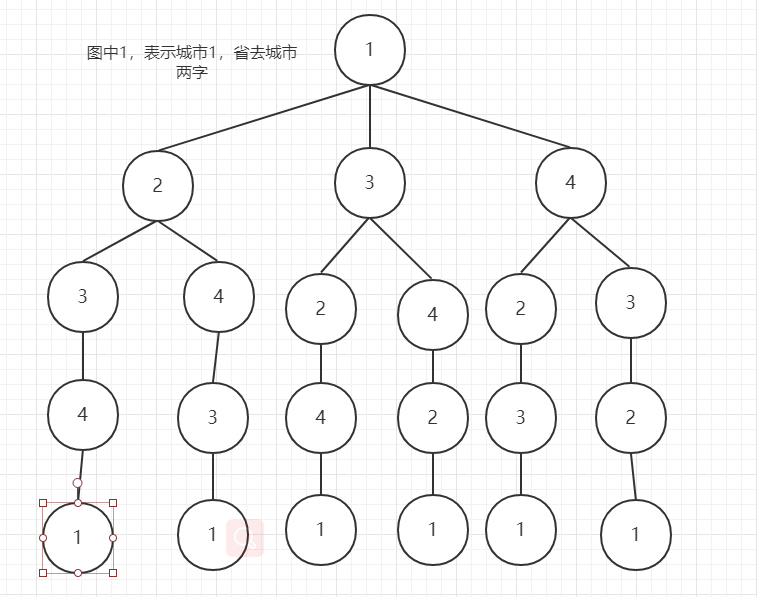
上面介绍回溯法就是把所有解列出来,然后剪枝深搜。那么我们需要解决的就是剪枝深搜了。剪枝深搜中最麻烦的就是找到何时剪枝的条件了。
首先我们假设不知道剪枝条件,先模拟深搜跑一遍。
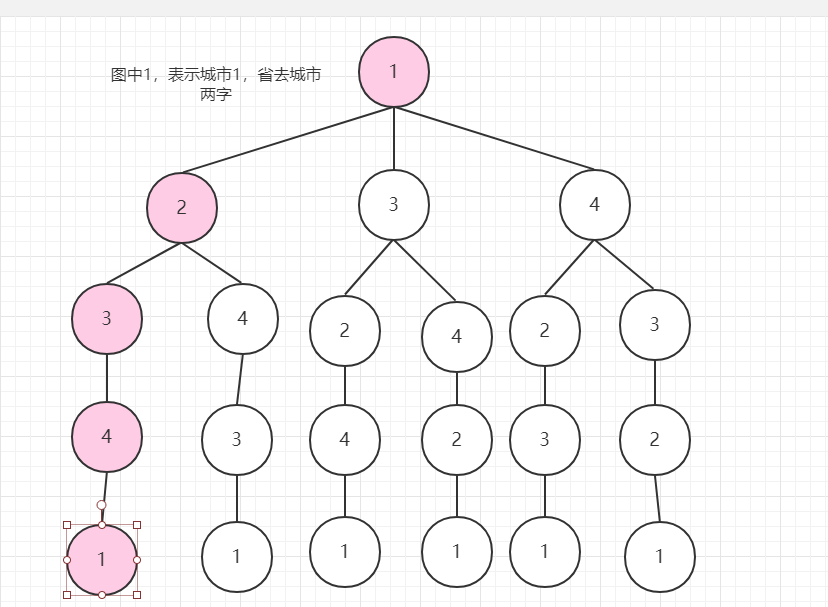
从1深搜到4回到1,花费11,记录这个数值。接下来回溯,继续深搜。一步一步深搜的时候,遇到了一个特殊的时候:
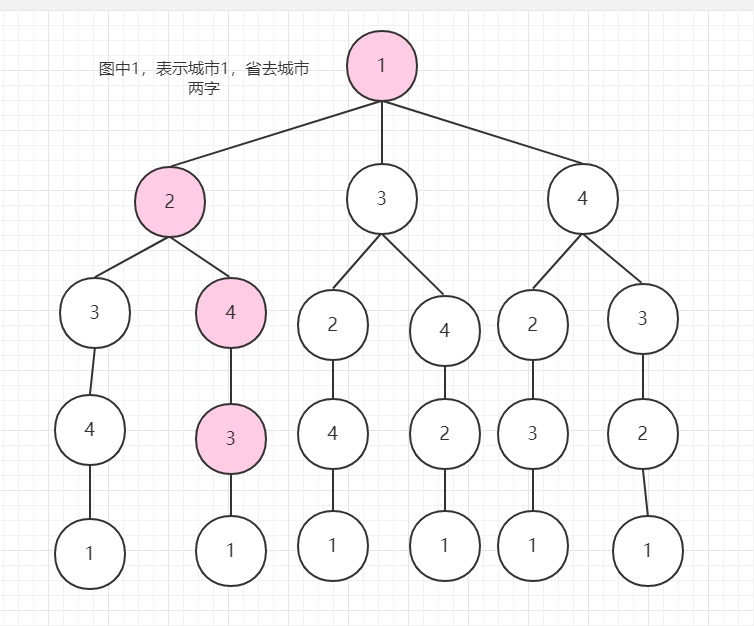
还记得我们之前记录的最短花费为11吗,1->2->4->3 花费已经11了,3回到1,还需要进行花费,不管花费多少,反正已经比我之前找出来的要大了,那这个时候我再深搜下去就没什么意义了,所以可以进行剪枝。我不继续找了,直接回溯。
所以剪枝条件出来了: 走下一步的距离 + 之前已经走过的距离的总和 >之前算出的最短路径 。
4.动态规划实现TSP
上面介绍了动态规划就是把大问题分解成小问题。我们现在的大问题是从1 经过2,3,4 回到1花费最少,那么我们把他分解一下。
我们从1出发有三种方案
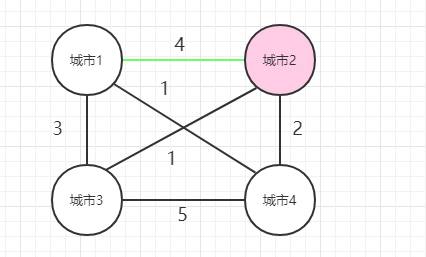
1、 从1出发,到2,然后再从2出发,经过[3,4]这几个城市,然后回到1,使得花费最少。
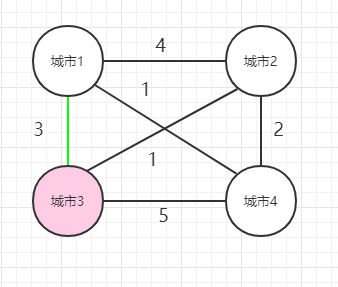
2、 从1出发,到3,然后再从3出发,经过[2,4]这几个城市,然后回到1,使得花费最少。
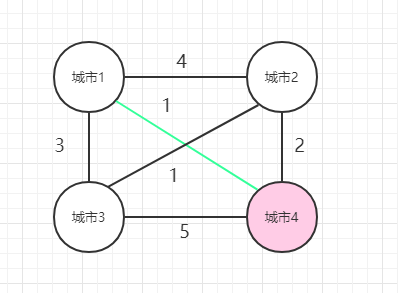
3、 从1出发,到4,然后再从4出发,经过[2,3]这几个城市,然后回到1,使得花费最少。
上面也提到了最优结果通过表来保留:设置一个二维的动态规划表dp , dp[1]{2,3,4}表示从1号城市出发,经过2,3,4 回到1花费最少。
要求上面三个方案的最小值意味:(D12表示1到2的距离,其他同理)
dp[1] [{2,3,4}] = min{ D12+dp[2]{3,4} ,D13+dp[3]{2,4} , D14+dp[4]{2,3}}
由于D12,D13,D14是已知的,那么我们现在的目的就是求dp[2]{3,4},dp[3]{2,4},dp[4]{2,3},
照猫画虎,我们可以列出:(这里只列出dp[2]{3,4} ,其他两个类似)
dp[2]{3,4} = min{ D23+dp[3]{4} ,D24+dp[4][3}}
dp[3]{4}]= D43+dp[4]{}
dp[4]{}=D41
那么经过慢慢的分解,我们知道了我们已知了从4到1的最小花费,那么就可以推出从3出发经过4回到1的花费。。。。。。。从而推出我们所要求的最优解。
5.时间复杂度分析
回溯法:
动态规划法: