题意:
给出一个$R imes C$的棋盘,其中$1$到$N$之间的每个正整数都会在棋盘上出现两次,第$i$个数出现的位置是$(X_{i,1},Y_{i,1})$和$(X_{i,2},Y_{i,2})$,现在目的是把每一对相同的数用线(粗细忽略不计)连起来,且线不能相交也不能越过棋盘边界,求是否能完成。
$1leq R,Cleq 10^8$
$1leq Nleq 10^5$
题解:
看上去是神仙题,实际上很假。。。
大家有没有玩过麻将连连看那种小游戏?题意中的连线意义就差不多。首先如果把这个棋盘扩展到无限大,即没有棋盘边界的限制,显然一定能满足条件。因为棋盘边上的数字连的线肯定可以在向外连足够远之后连回来,而内部的线由于可以跨越每个格子的边界,必定可以满足条件。(正确性感性理解一下?)
那么有了边界限制之后,就只用考虑在两个位置都在边界上的那些数字,把这些数字看成一对括号,如果整个边界上按顺序(顺时针或逆时针)能构成一个合法括号序列,那么就能满足,否则就不行。画个图感受一下:

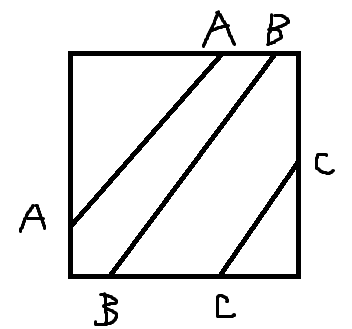
如图,左图是非法的而右图是合法的。那这个东西直接用栈判断一下就好了。。。先把所有位置排序,然后如果现在位置的数字和栈顶相等则弹出栈顶,否则把当前数字压入栈,最后判断栈是否为空即可。
ps:这题细节极其恶心!写挂了五六次才过样例。。。(可能是我写法比较挫)
代码:
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<cmath>
6 #include<queue>
7 #include<stack>
8 #define inf 2147483647
9 #define eps 1e-9
10 using namespace std;
11 typedef long long ll;
12 struct node{
13 int x,id;
14 }li[4][100001];
15 int r,c,n,x,y,xx,yy,nw,tot[4];
16 stack<int>st;
17 bool cmp1(node a,node b){
18 return a.x<b.x;
19 }
20 bool cmp2(node a,node b){
21 return a.x>b.x;
22 }
23 int main(){
24 scanf("%d%d%d",&r,&c,&n);
25 for(int i=1;i<=n;i++){
26 scanf("%d%d%d%d",&x,&y,&xx,&yy);
27 if((x&&y&&x!=r&&y!=c)||(xx&&yy&&xx!=r&&yy!=c))continue;
28 if(!x)nw=3;
29 else if(x==r)nw=1;
30 else if(!y)nw=0;
31 else if(y==c)nw=2;
32 if(nw==1||nw==3)li[nw][++tot[nw]]=(node){y,i};
33 else li[nw][++tot[nw]]=(node){x,i};
34 if(!xx)nw=3;
35 else if(xx==r)nw=1;
36 else if(!yy)nw=0;
37 else if(yy==c)nw=2;
38 if(nw==1||nw==3)li[nw][++tot[nw]]=(node){yy,i};
39 else li[nw][++tot[nw]]=(node){xx,i};
40 }
41 for(int i=0;i<4;i++){
42 if(i==0||i==1)sort(li[i]+1,li[i]+tot[i]+1,cmp1);
43 else sort(li[i]+1,li[i]+tot[i]+1,cmp2);
44 for(int j=1;j<=tot[i];j++){
45 if(!st.empty()&&li[i][j].id==st.top())st.pop();
46 else st.push(li[i][j].id);
47 }
48 }
49 if(st.empty())puts("YES");
50 else puts("NO");
51 return 0;
52 }