一个开关的开合状态可以对应“0、1”两个信号,莱布尼茨三百多年前留下的这个制式影响深远。日常语言依赖于思维逻辑,与之类似,数字语言的流通则依赖于数学逻辑,但本质上仍然只是无数个与非门的逻辑计算。因此相比于计算机,我们的计算能力虽然在效率方面有点难以启齿,但这并不代表有些事情我们注定办不到。
比如靠肉眼识别二维码?虽然人类大脑的计算效率早已落后家用计算机好几个量级,但这并不妨碍我们光靠人脑去完成一件“看似只有电子设备才能完成的事情”的尝试。
我们在生活中消费、转账时用手机扫的二维码,属于QR code(Quick Response)。但除了QR code之外,二维码还有其他多种制式标准,比如Data Matrix、PDF417、Ultra-code——本文只讨论QR码这个生活场景中最常见的二维码制,因为……其他的我也不会。
条码技术最早需要追溯到上世纪20年代,当时美国威斯汀豪斯(Westinghouse)实验室的发明家约翰·科芒德(John Kermode)为了实现对邮政单据的自动分检,发明了一种用条码对单据做标记的机制(一个条表示数字“1”,二个条表示数字“2”,称为模块比较法),以及相应的译码器。
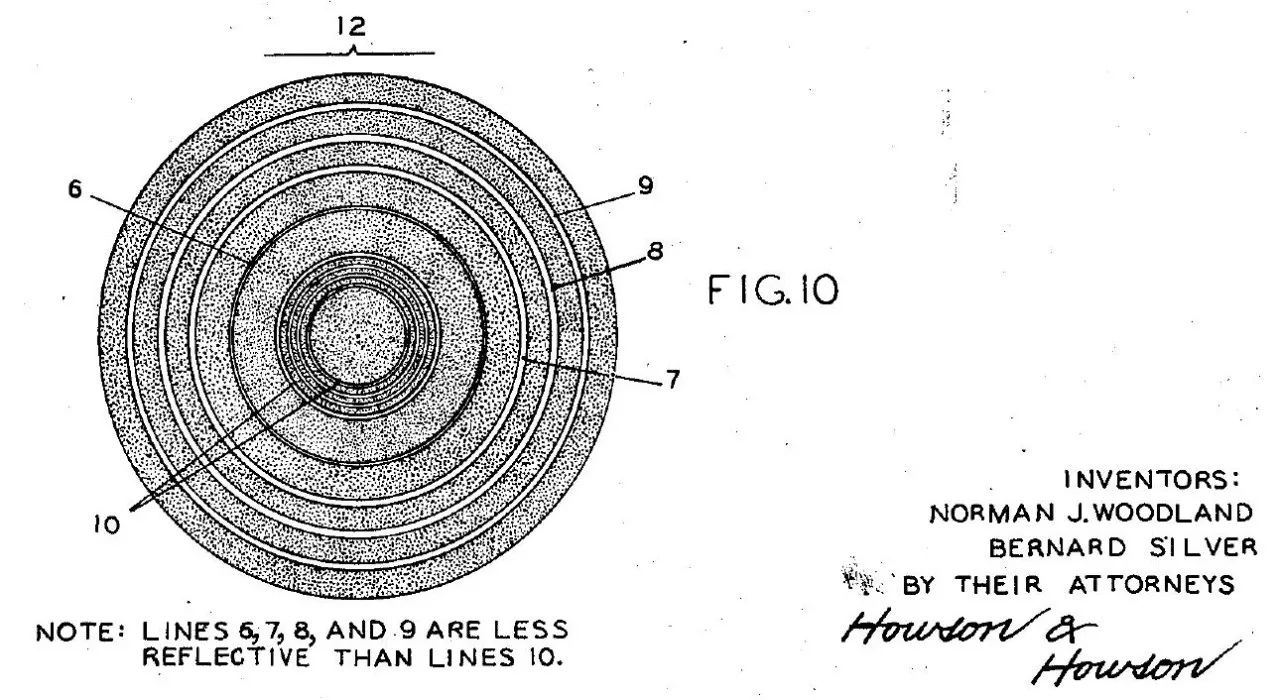
但是这种始祖鸟级别的制式所蕴含的信息量极低,不久后科芒德的合作者道格拉斯·杨(Douglas Young)对此进行了改进,利用黑条之间空隙的尺寸变化来编码数据。两人在1949年获得了世界上第一个条码专利,这种最早期的条码由黑白相间的同心圆组成,被称为牛眼式条码。
另一说法称,牛眼式条纹是由工程师诺曼·伍德兰(Norman J. Woodland)发明的
现如今,我们已经对扫码购物的行为非常习惯了,但在条码技术普及之前,超市的出纳员只能靠敲键盘来输入商品价格,操作成本高不说,患有腱鞘炎的人也不在少数,简直成了职业病。条码技术的出现无疑节省了很多工作成本,更何况条码本身也伴随着硬件技术实现一次次的更迭和普及。
欲求不满是人类的美好品德。条形码虽然带来了极大的便利,但是容量依旧有限,只容纳20个英文和数字,且无法编码汉字和假名。当时的制码人员几乎分成了两类,一类研究怎么往条码里塞更多的信息,一类研究怎么更快解码。大多数人属于第一类,而当时正在日本丰田子公司DensoWave从事条形码读取机研发的原昌宏开始尝试研发更快速的编码制式,进过一年半的研发过程,才有了1994年QR code码制的发明。
码如其名,这一码制的最大特点便是“Quick Response”——快速响应,读取速度比其他编码制式快10倍以上,最先被用在汽车零部件生产行业的电子看板管理(负责传递信息和生产管理的系统之一)中,大大提高了生产、出货乃至单据的管理效率。
作为一个男性程序员,原昌宏对于“快”有着独特的理解。他认为要想在应用条码的过程中实现快速,核心是解决识别的问题,剩下的内容只是计算。
——如何才能让机器快速找到目标码区?
用特殊形状的符号标记区域。——
——如何确定码区所在平面?
用三个特殊形状的标记(三点确定一个平面)。——
——如何确定机器读取码区的方向?
设置好从某一标记出发,以及出发的方向就可以了。——
逻辑没有问题,剩下要解决的就是标记的形状。如果编码周围有相同的图案,读取时就会被误认为是编码信息,从而导致误读,因此定位图案一定要保证特殊性。原昌宏为此收罗了大量广告单、杂志等印刷品,从各个方向进行扫描,并做了黑白色的二值处理,分析黑白占比,从而得出结论:黑白间隔比为1:1:3:1:1的比例定位的时,在印刷品中出现的概率最低。
以下方二维码为例,三个分别位于二维码的左上角、右上角、左下角的“回”字形符号,便是规定了尺寸、读取方向的位置探测图形。有这三个识别符号放在二维码的三个角上后,解码的时间响应就可以很快,比同时代的技术要快20倍。 这便是肉眼识别二维码所要了解的第一个知识点:
用位置探测图形确定码区。

此外,该制式还规定在与位置探测图形接壤的码区部分均为空白,以防止对位置探测图形产生识别干扰,这便是位置探测图形分隔符(下图中蓝色区域)。

再考虑到印有二维码的载体在实际应用场景中可能会发生的扭曲、移位和破损,制式还规定了一种与位置探测图形相类似的“回”字形图案(1:1:1:1:1),用来辅助定位减少误差,这便是校正图形(仅在版本2以上存在)。

但如果连校正图形也被污染了呢?还有定位图形(下图黄色区域),这是平行于二维码边缘的两条黑白交替出现的直线,与位置探测图形分隔符相接,用于确定二维码的角度,纠正扭曲。

上面介绍的四个图形均属于功能区域,都是为了保证QR码能被读码设备正确获取,不存储具体数据信息。在学习肉眼识别二维码的过程中,我们只要找得到它们就够了。
那么在剩下来的编码区里,究竟可以存储多少信息?答案是试规格而定。为了节省空间,QR码符号共有40种规格的矩阵,从最小的21x21(版本1)到最大177x177(版本40),每一版本符号比前一版本每边增加4个模块。版本1的二维码最多可以储存25个字符或41个数字,而版本40的二维码最多可以储存4296个字符或7089个数字。

在下图的版本1二维码中,只有未被红黄蓝三色填充的几块码区为我们所需要的数据存储区。信息将通过特定算法转换成黑色和白色的小方格填充其中,但即便我们知道了该看哪些区域,离最终解码还有些距离。

再往下细分,数据存储区又可以分成三类:数据编码、纠错编码,以及代表格式字符串的码区。第一种自然不必说,是我们最终需要使用的区域。至于纠错编码,这里不得不提到QR码的另外一大特点——高容错率。
日常生活里,沿街餐馆里贴在桌角用于收款的二维码大概是最容易受损的了。印有二维码的小纸片这边磨破一个角,那边沾了点酱油,码区可能早已不再完整。纠错编码的作用便体现在这里,通过对数据码进行RS纠错计算(里德-所罗门码算法)得到与之对应的纠错码,以此来保证二维码的可读性。当数据码区受到污染的时候,读码器依旧可以凭借纠错码得到正确信息。
根据纠错能力的不同,纠错码共分成L、M、Q、H 4个级别,分别可修正7%、15%、25%、30%的字码。关于纠错码的级别信息便记录在数据区的第三块内容——格式字符串中(即下图红色部分),这是我们需要处理的第一组数据。

格式字符串所蕴含的信息除了纠错等级以外,还包括表示掩码类型的信息。所谓的掩码,粗暴理解是为了让二维码更加容易被机器识别而定义的一次计算过程,降低了二维码本身被误读的可能性,使整个二维码码区排列更均匀,更容易被识别。
QR码制式中一共定义了7种掩码类型,每一种又可以根据4个纠错码级别产生4个变种,对于同一个信息便有了4*7=28种加工可能。因此只有确定了纠错等级和掩码类型,才能正式进入对数据的处理阶段,而我们首先需要得到的便是掩码的类型。
黑块为“1”,白块为“0”。格式字符串数据的翻译方向为从上往下(或从右到左),需注意当从右往左进行翻译的时候,右边半段红色区域的左端与左边半段红色区域的右端是重复信息,只取其中一位。基于上述算法法则,我们很快可以得到格式字符串信息(红色区域,如上图所示)——110011000101111,再查阅格式字符串表可得出结论:该二维码所采用的纠错级别为L,掩码模式4(下图正中所示掩码模式)。

接下来便需要对掩码进行逆向计算。所谓掩码其实很好理解——这是一个把数据区里的黑白小方块拆散的过程,每种掩码类型所规定的图像模型中,黑色区域表示原始码区的该位置需要颠倒一次黑白(数值反转),白色区域保持不变,以此来打散码区。因此我们可以根据掩码模式4的图形来推算这个二维码在掩码处理之前的状态。

终于等到从图形码变成数字的一刻。对于上图左侧我们得出的结论图,我们定义白块为0,黑块为1,从最右下角的模块开始进行记录,可以很轻易得到一串数列。下图是一个附带校正图形(紫色部分)与版本信息(蓝色部分)的二维码示意图,红线所示为阅读方向。
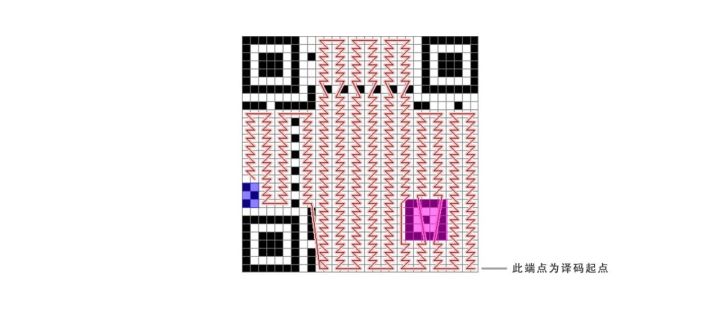
该数列为:
01000000 00110110
01010110 11100110
01000000 ……
接下来的工作便是对这串数字进行换算。无论是编码还是解码,我们都希望二维码能够以最短的比特串记录数据,因此编码开始之前便会对四种数据形式(数字、字母数字、汉字,8位字节)进行编码方式的选择,在后期得到的二进制数列中也能找到每一个编码方式独有的二进制标识,这些标识会记录在数据区的前端(即图中右下角四个小方块的位置),使得解码器可以根据二维码使用的编码方式对数据进行解码。
编码方式通常用4位数字表示,因此我们单拎出开头的4个数字“0100”,对照下表可查到对应的模式为字节模式。

8位字节模式所使用的是ASCII字符集,每个字符都需要用8位二进制码进行表示。而在代表编码模式的4个数字后面,我们仍需要再拎出来8个数字“00000011”,这组数字所表示的是原数据的字符数,十进制为3,即原数据共有三个字节。
因此这组数据应该这样排列:
0100 00000011
01100101 01101110
01100100 0000……
在二维码的解码过程中,“0000”代表的是原始数据的结束。但QR码对每种版本都规定了具体位数,因此后面的数据码往往由补齐码和大量纠错码组成。
补齐码的设置其实特别有意思。在终止符出现后,需要先将位数用“0”补到8的倍数。如果还不够,则需要往后头重复两组字节:11101100 、00010001。这些字节分别等于236和17,在二维码里的地位有如开普勒常数之于太阳系,自然常数之于自然。具体为何如此规定,若悉知,望告知。
至于纠错码,虽然本文不多做介绍,但是由于在大容量二维码中(版本高于4),最后呈现出来的码是通过将数据码和纠错码进行重新排布,再套用掩码模型制作出来的,因此无法用前文的方法进行计算。
最后的最后,我们最后倒腾出来的三组字节换算成10进制后分别是101、110、100,查询下表就可以看到这张二维码的数据信息,肉眼识别二维码——目标达成。