Python3 集合
集合(set)是一个无序的不重复元素序列。
可以使用大括号 { } 或者 set() 函数创建集合,注意:创建一个空集合必须用 set() 而不是 { },因为 { } 是用来创建一个空字典。
创建格式:
parame = {value01,value02,...}
或者
set(value)
集合的基本操作
集合内置方法完整列表
| 方法 | 描述 |
|---|---|
| add() | 为集合添加元素 |
| clear() | 移除集合中的所有元素 |
| copy() | 拷贝一个集合 |
| difference() | 返回多个集合的差集 |
| difference_update() | 移除集合中的元素,该元素在指定的集合也存在。 |
| discard() | 删除集合中指定的元素 |
| intersection() | 返回集合的交集 |
| intersection_update() | 返回集合的交集。 |
| isdisjoint() | 判断两个集合是否包含相同的元素,如果没有返回 True,否则返回 False。 |
| issubset() | 判断指定集合是否为该方法参数集合的子集。 |
| issuperset() | 判断该方法的参数集合是否为指定集合的子集 |
| pop() | 随机移除元素 |
| remove() | 移除指定元素 |
| symmetric_difference() | 返回两个集合中不重复的元素集合。 |
| symmetric_difference_update() | 移除当前集合中在另外一个指定集合相同的元素,并将另外一个指定集合中不同的元素插入到当前集合中。 |
| union() | 返回两个集合的并集 |
| update() | 给集合添加元素 |
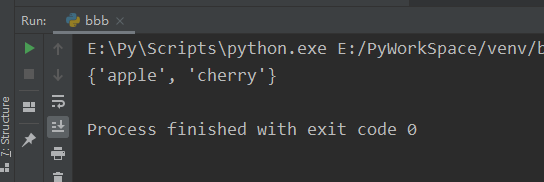
add()
fruits = {"apple", "banana", "cherry"}
fruits.add("orange")
print(fruits)
clear()
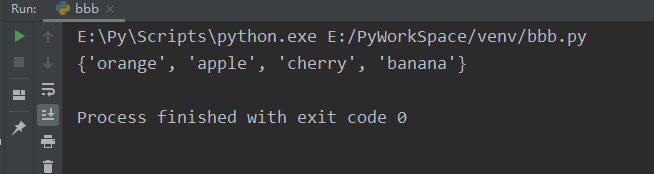
fruits = {"apple", "banana", "cherry"}
fruits.clear()
print(fruits)
copy()
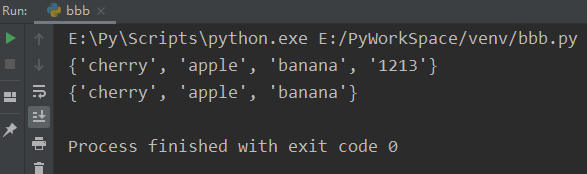
fruits = {"apple", "banana", "cherry"}
x = fruits.copy()
x.add('1213')
print(x)
print(fruits)
differenc()
x = {"apple", "banana", "cherry"}
y = {"google", "microsoft", "apple"}
z = x.difference(y)
print(z)
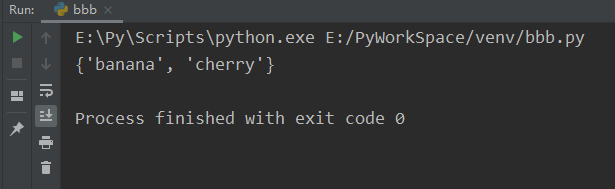
discard()
fruits = {"apple", "banana", "cherry"}
fruits.discard("banana")
print(fruits)

update()
x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "apple"}
x.update(y)
print(x)

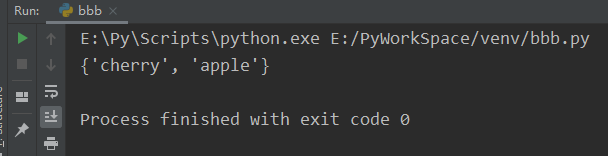
remove()
fruits = {"apple", "banana", "cherry"}
fruits.remove("banana")
print(fruits)
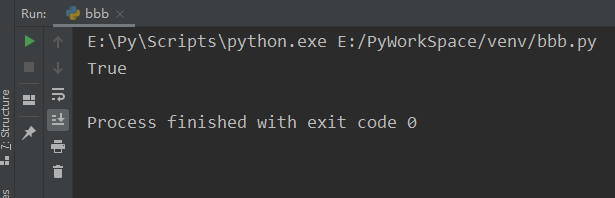
isdisjoint()
x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "facebook"}
z = x.isdisjoint(y)
print(z)
推荐用这种
discard() 方法用于移除指定的集合元素。
该方法不同于 remove() 方法,因为 remove() 方法在移除一个不存在的元素时会发生错误,而 discard() 方法不会。
fruits = {"apple", "banana", "cherry"}
fruits.discard("banana")
print(fruits)