Ellipse
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 2418 Accepted Submission(s): 1076
Problem Description
Math is important!! Many students failed in 2+2’s mathematical test, so let's AC this problem to mourn for our lost youth..
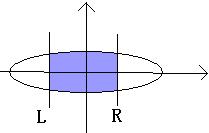
Look this sample picture:
Input
Input may contain multiple test cases. The first line is a positive integer N, denoting the number of test cases below. One case One line. The line will consist of a pair of integers a and b, denoting the ellipse equation
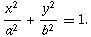 , A pair of integers l and r, mean the L is (l, 0) and R is (r, 0). (-a <= l <= r <= a).
, A pair of integers l and r, mean the L is (l, 0) and R is (r, 0). (-a <= l <= r <= a).Output
For each case, output one line containing a float, the area of the intersection, accurate to three decimals after the decimal point.
Sample Input
2
2 1 -2 2
2 1 0 2
6.283
3.142
#include<map>
#include<queue>
#include<math.h>
#include<vector>
#include<string>
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
#define inf 0x3f3f3f
#define ll long long
#define maxn 100005
using namespace std;
double a1,b1;
double F(double x) //这里自定义函数
{
return b1 * sqrt(1.0 - (x * x) / (a1 * a1));
}
double simpson(double a,double b) //返回区间[a,b]的三点辛普森值
{
double c = a + (b - a) / 2.0;
return (F(a) + 4 * F(c) + F(b)) * (b - a) / 6.0;
}
double asr(double a,double b,double eps,double A) //自适应辛普森递归过程
{
double c = a + (b - a) / 2.0; //A为区间[a,b]的三点辛普森值
double L = simpson(a,c), R = simpson(c,b);
if(fabs(L + R - A) <= 15 * eps) return L + R + (L + R - A) / 15.0;
return asr(a,c,eps/2.0,L) + asr(c,b,eps/2.0,R);
}
double asr(double a,double b,double eps) //自适应辛普森主过程
{
return asr(a,b,eps,simpson(a,b));
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
double l,r;
double eps=1e-5;
cin>>a1>>b1>>l>>r;
double ans=asr(l,r,eps);
ans*=2.0;
printf("%.3lf
",ans);
}
}