一、二分图的基本概念
【二分图】
二分图又称作二部图,是图论中的一种特殊模型。
设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
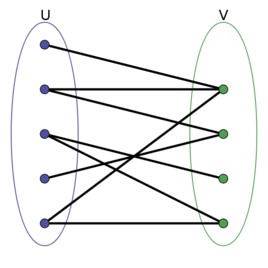
也就是说,只要两个点之间有边,那么这两个点就不能同属一个集合,必须分在两边。
这就带来一个问题,并不是所有的无向图G都能转化为二分图。
【二分图的判定】
定理:无向图G为二分图的充要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。
判定方法:根据定义比根据定理更好判定,只需要从第一个点出发,将其染成颜色1,则与其所有相连的所有终点都染成颜色2,如果与其相连的点已经被染成颜色1,则图G不是二分图。
把该点的所有终点当成新的起点,重复以上过程。很显然,既可以用dfs染色,又可以用bfs染色。
dfs染色代码:
#include<iostream> #include<vector> #include<cstring> using namespace std; const int maxn = 10010; int n,m;//顶点数 边数 vector<int> G[maxn]; int color[maxn] ; //0 没染色 1 -1不同色 bool dfs(int u, int c){ color[u] = c; for(int i=0; i<G[u].size(); i++){ int v = G[u][i]; if(color[v] == c) return false; if(color[v] == 0 && !dfs(v,-c)) return false; } return true; } bool solve(){ for(int i=1; i<=n; i++){ if(color[i] == 0) if(!dfs(i,1)){ return false; } } return true; } int main(){ int t; cin>>t; while(t--){ cin >> n >> m; memset(color, 0, sizeof(color)); for(int i=0; i<maxn; i++) G[i].clear(); for(int i = 0; i < m; i++) { int s, t; cin >> s >> t; G[s].push_back(t); G[t].push_back(s); // 如果有向图则无需这一句 } if(solve()){ cout<<"Correct"<<endl; } else cout<<"Wrong"<<endl; } return 0; }
bfs染色代码
// 使用邻接矩阵 int G[maxn][maxn]; bool bfs(int s) { color[s] = 1; queue<int> que; que.push(s); while(!que.empty()) { int from = que.front(); que.pop(); for(int i = 1; i <= V; i++) { // 如果相邻的点没有上色就给这个点上色 if(G[from][i] && color[i] == 0) { que.push(i); color[i] = -color[from]; } // 如果相邻的颜色相同则返回false if(G[from][i] && color[i] == color[from]) return false; } } // 如果所有的点都被染过色,且相邻的点颜色都不一样,返回true return true; }
二、二分图最大匹配
定义:在一个无向图中,定义一条边覆盖的点为这条边的两个端点。
找到一个边集S包含最多的边,使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。S的大小叫做图的最大匹配。
通俗地讲,比如说有一场宴会,男孩和女孩跳舞,并且他们必须互相喜欢才能一起跳舞,一个男孩可能喜欢0个或多个女孩,一个女孩也可能喜欢0个或多个男孩,但一个男孩和他喜欢地女孩跳舞之后就不能和其他他喜欢地女孩跳舞,女孩亦是如此。请问最多可以多少对男孩女孩一起跳舞。
很显然,互相喜欢的男孩和女孩建边得到一个二分图,求一个一个边集S包含最多的边,使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。即求二分图的最大匹配。
【匈牙利算法】
把二分图分为A,B两个集合,依次枚举A中的每个点,试图在B集合中找到一个匹配。
对于A集合中一点x,假设B集合中有一个与其相连的点y,若y暂时还没有匹配点,那么x可以和y匹配,找到;
否则,设y已经匹配的点为z(显然z是A集合中的一个点),那么,我们将尝试为z找到一个除了y之外的匹配点,若找到,那么x可以和y匹配,否则x不能与y匹配。
【图解】来自博客:https://www.cnblogs.com/jianglangcaijin/p/6035950.html
我们以下图为例说明匈牙利匹配算法。
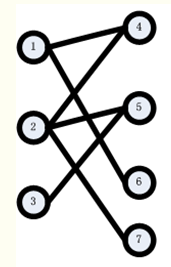
step1:从1开始,找到右侧的点4,发现点4没有被匹配,所以找到了1的匹配点为4 。得到如下图:
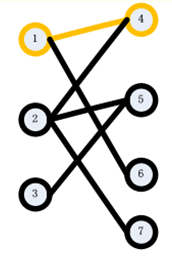
step2:接下来,从2开始,试图在右边找到一个它的匹配点。我们枚举5,发现5还没有被匹配,于是找到了2的匹配点,为5.得到如下图:
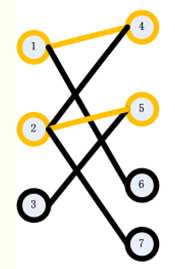
step3:接下来,我们找3的匹配点。我们枚举了5,发现5已经有了匹配点2。此时,我们试图找到2除了5以外的另一个匹配点,我们发现,我们可以找到7,于是2可以匹配7,所以5可以匹配给3,得到如下图:
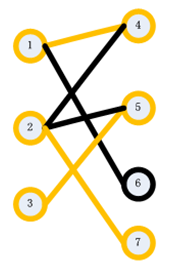
此时,结束,我们得到最大匹配为3。
【算法核心】
每次寻找可以匹配A点的一个点B,如果这个点B还没有被匹配,暂时就把这个点B当作A的匹配点;如果这个B在之前已经匹配了C,那就看C能不能匹配除了B以外的未匹配点,如果找不到则重复以上过程直到找到或者枚举所有可能点还找不到,结束点A的匹配;如果找到,则把B匀给A(本来B是C的,现在C说我还有其他舞伴,B就让给A了)。这样就能多出一个匹配,相当于找到一条“增广路径”。
【匈牙利算法模板】详见博客https://www.cnblogs.com/penseur/archive/2013/06/16/3138981.html
poj 1469 COURSES
已知,有N个学生和P门课程,每个学生可以选0门,1门或者多门课程,要求在N个学生中选出P个学生使得这P个学生与P门课程一一对应。
DFS

#include<iostream> #include<queue> #include<list> #include<vector> #include<cstring> #include<set> #include<stack> #include<map> #include<cmath> #include<algorithm> #include<string> #include<stdio.h> using namespace std; typedef long long ll; #define MS(x,i) memset(x,i,sizeof(x)) #define rep(i,s,e) for(int i=s; i<=e; i++) #define sc(a) scanf("%d",&a) #define scl(a) scanf("%lld",&a) #define sc2(a,b) scanf("%d %d", &a, &b) #define debug printf("debug...... "); #define pfd(x) printf("%d ",x) #define pfl(x) printf("%lld ",x) const double eps=1e-8; const double PI = acos(-1.0); const int inf = 0x3f3f3f3f; const ll INF = 0x7fffffff; const int maxn = 5e2+10; int dx[4] = {0, 0, 1, -1}; int dy[4] = {1, -1, 0 , 0}; int match[maxn];//匹配 vector<int> G[maxn]; bool vis[maxn]; int n, m; bool dfs(int u) { for(int i=0; i<G[u].size(); i++){ int v = G[u][i]; if(!vis[v]){ vis[v] = 1; if(match[v] == -1 || dfs(match[v])){ match[v] = u; return true; } } } return false; } void solve(){ int ans = 0; MS(match, -1); for(int i = 1; i <= n; i++){ MS(vis, 0); if(dfs(i)) ans++; } // printf("%s ", ans==n ? "YES":"NO"); if( ans == n) printf("YES "); else printf("NO "); } int main() { int t; sc(t); while(t--){ int k,c; sc2(n,m); rep(i,0,n) G[i].clear(); rep(i,1,n){ sc(k); while(k--){ sc(c); G[i].push_back(c); } } solve(); } }
【Hopcroft-Karp算法】
利用匈牙利算法一次只能找到一条增广路径,Hopcroft-Karp就提出一次找到多条不相交的增广路径(不相交就是没有公共点和公共边的增广路径),然后根据这些增广路径添加多个匹配。

【Hopcroft-Karp算法模板】

#include<iostream> #include<queue> using namespace std; const int MAXN=500;// 最大点数 const int INF=1<<28;// 距离初始值 int bmap[MAXN][MAXN];//二分图 int cx[MAXN];//cx[i]表示左集合i顶点所匹配的右集合的顶点序号 int cy[MAXN]; //cy[i]表示右集合i顶点所匹配的左集合的顶点序号 int nx,ny; int dx[MAXN]; int dy[MAXN]; int dis; bool bmask[MAXN]; //寻找 增广路径集 bool searchpath() { queue<int>Q; dis=INF; memset(dx,-1,sizeof(dx)); memset(dy,-1,sizeof(dy)); for(int i=1;i<=nx;i++) { //cx[i]表示左集合i顶点所匹配的右集合的顶点序号 if(cx[i]==-1) { //将未遍历的节点 入队 并初始化次节点距离为0 Q.push(i); dx[i]=0; } } //广度搜索增广路径 while(!Q.empty()) { int u=Q.front(); Q.pop(); if(dx[u]>dis) break; //取右侧节点 for(int v=1;v<=ny;v++) { //右侧节点的增广路径的距离 if(bmap[u][v]&&dy[v]==-1) { dy[v]=dx[u]+1; //v对应的距离 为u对应距离加1 if(cy[v]==-1) dis=dy[v]; else { dx[cy[v]]=dy[v]+1; Q.push(cy[v]); } } } } return dis!=INF; } //寻找路径 深度搜索 int findpath(int u) { for(int v=1;v<=ny;v++) { //如果该点没有被遍历过 并且距离为上一节点+1 if(!bmask[v]&&bmap[u][v]&&dy[v]==dx[u]+1) { //对该点染色 bmask[v]=1; if(cy[v]!=-1&&dy[v]==dis) { continue; } if(cy[v]==-1||findpath(cy[v])) { cy[v]=u;cx[u]=v; return 1; } } } return 0; } //得到最大匹配的数目 int MaxMatch() { int res=0; memset(cx,-1,sizeof(cx)); memset(cy,-1,sizeof(cy)); while(searchpath()) { memset(bmask,0,sizeof(bmask)); for(int i=1;i<=nx;i++) { if(cx[i]==-1) { res+=findpath(i); } } } return res; } int main() { int num; scanf("%d",&num); while(num--) { memset(bmap,0,sizeof(bmap)); scanf("%d%d",&nx,&ny); for(int i=1;i<=nx;i++) { int snum; scanf("%d",&snum); int u; for(int j=1;j<=snum;j++) { scanf("%d",&u); bmap[i][u]=1; // bmap[u][i]=1; } } // cout<<MaxMatch()<<endl; if(MaxMatch()==nx) { printf("YES "); } else { printf("NO "); } } //system("pause"); return 0; } /* 4 1 3 1 3 4 2 */
三、二分图最小顶点覆盖
定义:假如选了一个点就相当于覆盖了以它为端点的所有边。最小顶点覆盖就是选择最少的点来覆盖所有的边。
定理:最小顶点覆盖等于二分图的最大匹配。
四、最大独立集
定义:选出一些顶点使得这些顶点两两不相邻,则这些点构成的集合称为独立集。找出一个包含顶点数最多的独立集称为最大独立集。
定理:最大独立集 = 所有顶点数 - 最小顶点覆盖 = 所有顶点数 - 最大匹配
【模板】
建边是相反意义建边,把有冲突关系的两个点建边,再套用最大匹配的模板,用所有顶点数减之即可。
【代码】

#include <iostream> #include <cstdio> #include <cstring> #include <queue> #include <vector> #define INF 0x3f3f3f3f using namespace std; const int MAXN = 40005; int n;//顶点数 vector<int>prime; int vis[500005]; int num[MAXN],p[2][500005]; vector<int> G[MAXN],v[MAXN]; int Mx[MAXN],My[MAXN]; int dx[MAXN],dy[MAXN]; int dis; bool used[MAXN];//DFS中甬道的访问标记 void get_prime(){ memset(vis,0,sizeof(vis)); prime.clear(); for(int i = 2; i <= 500000; i++){ int tt = 500000/i; for(int j = 2; j <= tt; j++) vis[i*j] = 1; } for(int i = 2; i <= 500000; i++){ if(!vis[i]) prime.push_back(i); } } void init(){ for(int i = 0; i <= n; i++){ G[i].clear(); v[i].clear(); } } bool SearchP(){ queue<int> q; dis = INF; memset(dx,-1,sizeof(dx)); memset(dy,-1,sizeof(dy)); for(int i = 0 ; i < n; i++){ if(Mx[i] == -1){ q.push(i); dx[i] = 0; } } while(!q.empty()){ int u = q.front(); q.pop(); if(dx[u] > dis) break; int l = G[u].size(); for(int i = 0; i < l; i++){ int v = G[u][i]; if(dy[v] == -1){ dy[v] = dx[u] + 1; if(My[v] == -1) dis = dy[v]; else{ dx[My[v]] = dy[v] + 1; q.push(My[v]); } } } } return dis != INF; } bool dfs(int u){ int l = G[u].size(); for(int i = 0; i < l; i++){ int v = G[u][i]; if(!used[v] && dy[v] == dx[u] + 1){ used[v] = true; if(My[v] != -1 && dy[v] == dis) continue; if(My[v] == -1 || dfs(My[v])){ My[v] = u; Mx[u] = v; return true; } } } return false; } int MaxMatch(){ int res = 0; memset(Mx, -1, sizeof(Mx)); memset(My, -1, sizeof(My)); while(SearchP()){ memset(used, false, sizeof(used)); for(int i = 0; i < n; i++) if(Mx[i] == -1 && dfs(i)) res++; } return res; } int main(){ get_prime(); int T,t = 1; scanf("%d",&T); while(T--){ scanf("%d",&n); init(); memset(p,0,sizeof(p)); for(int i = 1; i <= n; i++){ scanf("%d",&num[i]); int t = num[i],cnt = 0; for(int j = 0; prime[j]*prime[j] <= t; j++){ if(t % prime[j] == 0){ v[i].push_back(prime[j]); while(t%prime[j] == 0) cnt++,t /= prime[j]; } } if(t > 1){ v[i].push_back(t); cnt++; } p[cnt&1][num[i]] = i; } for(int i = 1; i <= n; i++){ if(p[0][num[i]]){ for(int j = 0; j < v[i].size(); j++){ int tmp = num[i]/v[i][j]; if(!p[1][tmp]) continue; G[i-1].push_back(p[1][tmp-1]); } } else{ for(int j = 0; j < v[i].size(); j++){ int tmp = num[i]/v[i][j]; if(!p[0][tmp]) continue; G[p[0][tmp]-1].push_back(i-1); } } } printf("Case %d: %d ",t++,n-MaxMatch()); } return 0; }
