错误率:错分样本的占比。如果在m个样本中有a个样本分类错误,则错误率为E=a/m;相应的,1-a/m称为“精度”,即“精度=1-错误率”
误差:样本真实输出与预测输出之间的差异。
训练(经验)误差:训练集上;测试误差:测试集;泛化误差:除训练集外所有样本
过拟合:学习器把训练样本学习的“太好”,将训练样本本身的特点当作所有样本的一般性质,导致泛化性能下降。(机器学习面临的关键障碍,优化目标加正则项、early stop)
欠拟合:对训练样本的一般性质尚未学好。(决策树:拓展分支,神经网络:增加训练轮数)
评估方法:
现实任务中往往会对学习器的泛化性能、时间开销、存储开销、可解释性等方面的因素进行评估并作出选择。
通常将包含m个样本的数据集D={(x1,y1),(x2,y2),...,(xm,ym)}拆分成训练集S和测试集T:
留出法:
直接将数据集划分为两个互斥集合
训练/测试集划分要尽可能保持数据分布的一致性
一般若干次随机划分、重复实验取平均值
训练/测试样本比例通常为2:1~4:1
交叉验证法:
将数据集分层采样划分为k个大小相似的互斥子集,每次用k-1个子集的并集作为训练集,余下的子集作为测试集,最终返回k个测试结果的均值,k最常用的取值是10.
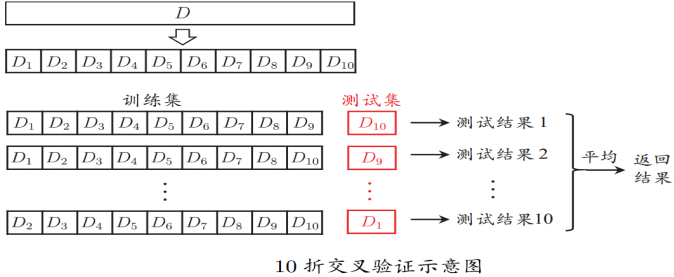
与留出法类似,将数据集D划分为k个子集同样存在多种划分方式,为了减小因样本划分不同而引入的差别,k折交叉验证通常随机使用不同的划分重复p次,最终的评估结果是这p次k折交叉验证结果的均值,例如常见的“10次10折交叉验证”
假设数据集D包含m个样本,若令k=m,则得到留一法:
不受随机样本划分方式的影响
结果往往比较准确
当数据集比较大时,计算开销难以忍受
自助法:
以自助采样法为基础,对数据集D有放回采样m次得到训练集D',DD'用做测试集。
实际模型与预期模型都使用m个训练样本
约有1/3的样本没在训练集中出现
从初始数据集中产生多个不同的训练集,对集成学习有很大的好处
自助法在数据集较小、难以有效划分训练/测试集时很有用;由于改变了数据集分布可能引入估计偏差,在数据量足够时,留出法和交叉验证法更常用。
评估分类器性能的度量
正元组(正样本):感兴趣的主要类的元组,P是正元组数。
负元组(负样本):其他元组,N是负元组数。
混淆矩阵(confusion matrix):
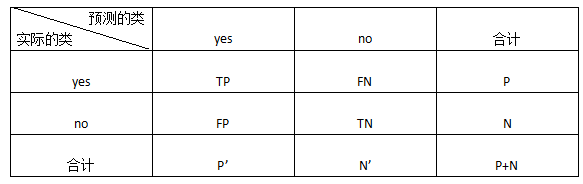
TP(True Positive):真正例/真阳性,是指被分类器正确分类的正元组
TN(True Negative):真负例/真阴性,是指被分类器正确分类的负元组
FP(False Positive):假正例/假阳性,是被错误地标记为正元组的负元组
FN(False Negative):假负例/假阴性,是被错误地标记为负元组的正元组
P’:被分类器标记为正的元组数(TP+FP)
N’:被分类器标记为负的元组数(TN+FN)
元组的总数=TP+TN+FP+FN=P+N=P'+N’
准确率(accuracy):被分类器正确分类的元组所占的百分比,准确率又称为分类器的总体识别率,即它反映分类器对各类元组的正确识别情况,当类分布相对平衡时最有效。即
accuracy=(TP+TN)/(P+N)
错误率(error rate,误分类率):error rate=(FP+FN)/(P+N)=1-accuracy
灵敏性(sensitivity)、真正例率(正确识别的正元组的百分比):sensitivity=TP/P
特效性(specificity)、真负例率(正确识别的负元组的百分比):specificity=TN/N
准确率是灵敏性和特效性度量的函数:accuracy=(TP+TN)/(P+N)=TP/(P+N)*(P/P)+TN/(P+N)*(N/N)=sensitivity*P/(P+N)+specificity*N/(P+N)
精度(precision):可以看作精确性的度量(标记为正类的元组实际为正类所占的百分比) precision=TP/(TP+FP)
召回率(recall):完全性的度量(正元组标记为正的百分比),就是灵敏度 recall=TP/(TP+FN)=TP/P=sensitivity

除了基于准确率的度量外,还可以根据其他方面比较分类器:
速度:涉及产生和使用分类器的计算开销
鲁棒性:这是假定数据有噪声或有缺失值时分类器做出正确预测的能力。通常,鲁棒性用噪声和缺失值渐增的一系列合成数据集评估。
可伸缩性:这涉及给定大量数据,有效地构造分类器的能力。通常,可伸缩性用规模渐增的一系列数据集评估。
可解释性:这涉及分类器或预测器提供的理解和洞察水平。可解释性是主观的,很难评估。
当数据类比较均衡地分布时,准确率效果最好,其他度量,如灵敏度(或召回率)、特效性、精度、F和Fβ更适合不平衡问题。
P-R曲线
查准率-查全率曲线,以查准率为纵轴,查全率为横轴作图。
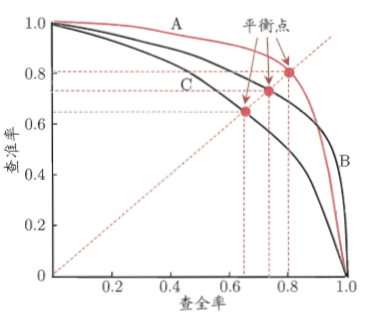
若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”,则后者性能优于前者,上图中学习器A的性能优于学习器C;如果两个学习器的P-R曲线发生了交叉,则需要比较P-R曲线下面积的大小,但这个面积不容易估算,通常综合考虑查准率、查全率的性能度量“平衡点(Break-Event Point,BEP)”,它是“查准率=查全率”时的取值。但BEP还是过于简化,更常用的是前面提到的F1度量。
ROC与AUC
“最可能”是正例的样本排在最前面,“最不可能”是正例的排在最后面,按此排序。分类的过程就相当于在排序中以某个“截断点(cut point)”将样本分为两部分,前一部分判断正例,后一部分为反例。不同任务中根据需求划分截断点;重视查准率(精度),靠前位置截断;重视查全率(召回率),靠后位置截断。
ROC(Receiver Operating Characteristic,受试者工作特征)曲线是一种比较两个分类模型有用的可视化工具。ROC曲线显示了给定模型的真正例率(TPR)和假正例率(FPR)之间的权衡,纵轴是“真正例率(TPR)”,横轴是“假正例率(FPR)”。

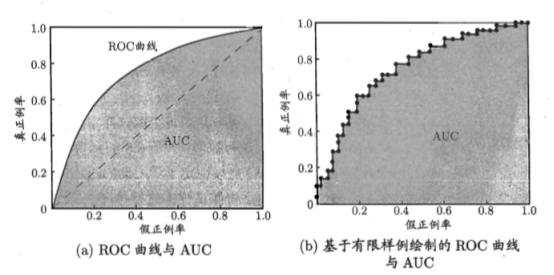
图(a)中,给出了两条线,ROC曲线给出的是当阈值变化时假正例率和真正例率的变化情况。左下角的点所对应的是将所有样例判为反例的情况,而右上角的点对应的则是将所有样例判为正例的情况。虚线给出的是随机猜测的结果曲线。
现实任务中通常利用有限个测试样例来绘制ROC图,此时仅能获得有限个(真正例率,假正例率)坐标对,无法产生图(a)中光滑的ROC曲线,只能绘制如图(b)所示的近似ROC曲线。
绘图过程:给定m+个正例和m-个反例,根据学习器预测结果对样例进行排序,然后把分类阈值设为最大,即把所有样例均预测为反例,此时真正例率和假正例率均为0,在坐标(0,0)处标记一个点。然后,将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例。设前一个标记点坐标为(x,y),当前若为真正例,则对应标记点的坐标为(x,y+1/m+);当前若为假正例,则对应标记点的坐标为(x+1/m-,y),然后用线段连接相邻点即可。
若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者性能优于前者;如果曲线交叉,可以根据ROC曲线下面积大小进行比较,也即AUC(Area Under ROC Curve)值.
AUC可通过对ROC曲线下各部分的面积求和而得。假定ROC曲线由坐标为{(x1,y1),(x2,y2),...,(xm,ym)}的点按序连接而形成(x1=0,xm=1),则AUC可估算为
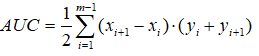
AUC给出的是分类器的平均性能值,它并不能代替对整条曲线的观察。一个完美的分类器的AUC为1.0,而随机猜测的AUC值为0.5
AUC考虑的是样本预测的排序质量,因此它与排序误差有紧密联系。给定m+个正例,m-个反例,令D+和D-分别表示正、反例集合,则排序”损失”定义为
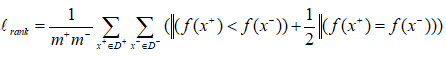
Lrank对应ROC曲线之上的面积:若一个正例在ROC曲线上标记为(x,y),则x恰是排序在期前的所有反例所占比例,即假正例,因此:
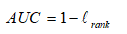
AUC值是一个概率值,当你随机挑选一个正样本以及负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值,AUC值越大,当前分类算法越有可能将正样本排在负样本前面,从而能够更好地分类。
代价敏感错误率和代价曲线
现实任务中不同类型的错误所造成的后果很可能不同,为了权衡不同类型错误所造成的不同损失,可为错误赋予“非均等代价”。
以二分类为例,可根据领域知识设定“代价矩阵”,如下表所示,其中costij表示将第i类样本预测为第j类样本的代价。一般来说,costii=0;若将第0类判别为第1类所造成的损失更大,则cost01>cost10;损失程度越大,cost01与cost10值的差别越大。
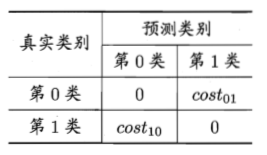
在非均等代价下,不再最小化错误次数,而是最小化“总体代价”,则“代价敏感”错误率相应的为:
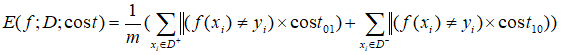
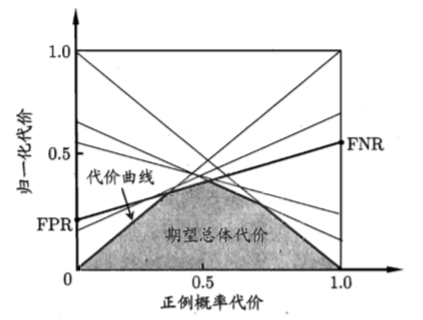
在非均等代价下,ROC曲线不能直接反映出学习器的期望总体代价,而“代价曲线(cost curve)”可以。代价曲线图的横轴是取值为[0,1]的正例概率代价
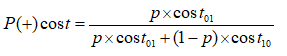
其中p是样例为正例的概率;纵轴是取值为[0,1]的归一化代价
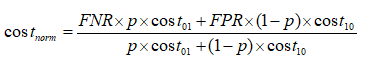
其中FPR是假正例率,FNR=1-TPR是假反例率。
代价曲线的绘制:ROC曲线上每个点对应了代价曲线上的一条线段,设ROC曲线上点的坐标为(TPR,FPR),则可相应计算出FNR,然后在代价平面上绘制一条从(0,FPR)到(1,FNR)的线段,线段下的面积即表示了该条件下的期望总体代价;如此将ROC曲线上的每个点转化为代价平面上的一条线段,然后取所有线段的下界,围成的面积即为所有条件下学习器的期望总体代价。