首先,我们继续上一篇文章中的例子,在这里我们增加一个特征,也即卧室数量,如下表格所示:

因为在上一篇中引入了一些符号,所以这里再次补充说明一下:
x‘s:在这里是一个二维的向量,例如:x1(i)第i间房子的大小(Living area),x2(i)表示的是第i间房子的卧室数量(bedrooms).
在我们设计算法的时候,选取哪些特征这个问题往往是取决于我们个人的,只要能对算法有利,尽量选取。
对于假设函数,这里我们用一个线性方程(在后面我们会说到运用更复杂的假设函数):hΘ(x) = Θ0+Θ1x1+Θ2x2
这里,θi为参数,也称为权值(weights)。我们假定x0 = 1。因此上述可以表示为矩阵形式:
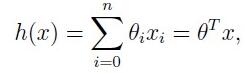

梯度下降法是按下面的流程进行的:
1)首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量。
2)改变θ的值,使得J(θ)按梯度下降的方向进行减少。
如下图:

上图表示的是参数Θ和代价函数J(Θ)的关系图,深蓝色为全局最小,浅蓝色为局部最小,红色则表示J(Θ)有一个较大的取值,而梯度下降算法就是我们给定一个初始的Θ值,然后按照梯度下降的原则不断更新Θ值,使得J(Θ)向更低的方向进行移动。算法的结束将是在θ下降到无法继续下降为止。上面两条线代表我们给定两个初值,我们发现一条到达局部最小,即浅蓝色,而一条到达全局最小,即深蓝色。所以从这里我们可以看出,初始值的选择对梯度下降的影响很大。


如果 α 太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛, 下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,所以,如果 α 太大,它会导致无法收敛,甚至发散。
批量梯度下降算法(batch gradient descent)



随机梯度下降算法(stochastic gradient descent)
当样本集数据量m很大时,由于每次在进行批量梯度下降时都需要用到所有的训练样本,所以开销就会很大,这个时候我们更多时候使用随机梯度下降算法(stochastic gradient descent),算法如下所示:

在进行随机梯度下降算法时,我们每次迭代都只选取一个训练样本,这样当我们迭代到若干样本的时候Θ就已经迭代到最优解了。
正规方程(The Normal equations)
梯度下降给我们提供了一种最小化J的方法,除了梯度下降,正规方程也是一种很好求解Θ的方法,这里只给出结论,如下
