概念
凸包(Convex Hull)是一个计算几何(图形学)中的概念。用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边型,它能包含点集中所有点的。严谨的定义和相关概念参见维基百科:凸包。
这个算法是由数学大师葛立恒(Graham)发明的,他曾经是美国数学学会(AMS)主席、AT&T首席科学家以及国际杂技师协会(IJA)主席。(太汗了,这位大牛还会玩杂技~)
问题
给定平面上的二维点集,求解其凸包。
过程
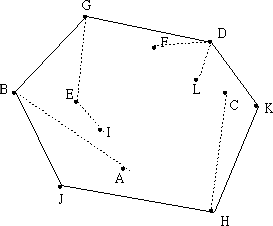
1. 在所有点中选取y坐标最小的一点H,当作基点。如果存在多个点的y坐标都为最小值,则选取x坐标最小的一点。坐标相同的点应排除。然后按照其它各点p和基点构成的向量<H,p>与x轴的夹角进行排序,夹角由大至小进行顺时针扫描,反之则进行逆时针扫描。实现中无需求得夹角,只需根据向量的内积公式求出向量的模即可。以下图为例,基点为H,根据夹角由小至大排序后依次为H,K,C,D,L,F,G,E,I,B,A,J。下面进行逆时针扫描。

2. 线段<H, K>一定在凸包上,接着加入C。假设线段<K, C>也在凸包上,因为就H,K,C三点而言,它们的凸包就是由此三点所组成。但是接下来加入D时会发现,线段<K, D>才会在凸包上,所以将线段<K, C>排除,C点不可能是凸包。
3. 即当加入一点时,必须考虑到前面的线段是否会出现在凸包上。从基点开始,凸包上每条相临的线段的旋转方向应该一致,并与扫描的方向相反。如果发现新加的点使得新线段与上线段的旋转方向发生变化,则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断,设新加入的点为pn + 1,上一点为pn,再上一点为pn - 1。顺时针扫描时,如果向量<pn - 1, pn>与<pn, pn + 1>的叉积为正(逆时针扫描判断是否为负),则将上一点删除。删除过程需要回溯,将之前所有叉积符号相反的点都删除,然后将新点加入凸包。
在上图中,加入K点时,由于线段<H,K>相对于<H,C>为顺时针旋转,所以C点不在凸包上,应该删除,保留K点。接着加入D点,由于线段<K, D>相对<H, K>为逆时针旋转,故D点保留。按照上述步骤进行扫描,直到点集中所有的点都遍例完成,即得到凸包。
复杂度
这个算法可以直接在原数据上进行运算,因此空间复杂度为O(1)。但如果将凸包的结果存储到另一数组中,则可能在代码级别进行优化。由于在扫描凸包前要进行排序,因此时间复杂度至少为快速排序的O(nlgn)。后面的扫描过程复杂度为O(n),因此整个算法的复杂度为O(nlgn)。
C++/STL实现
#include <algorithm>#include <iostream>#include <vector>#include <math.h>using namespace std;//二维点(或向量)结构体定义#ifndef _WINDEF_struct POINT { int x; int y; };#endiftypedef vector<POINT> PTARRAY;//判断两个点(或向量)是否相等bool operator==(const POINT &pt1, const POINT &pt2) { return (pt1.x == pt2.x && pt1.y == pt2.y);}// 比较两个向量pt1和pt2分别与x轴向量(1, 0)的夹角bool CompareVector(const POINT &pt1, const POINT &pt2) { //求向量的模 float m1 = sqrt((float)(pt1.x * pt1.x + pt1.y * pt1.y)); float m2 = sqrt((float)(pt2.x * pt2.x + pt2.y * pt2.y)); //两个向量分别与(1, 0)求内积 float v1 = pt1.x / m1, v2 = pt2.x / m2; return (v1 > v2 || (v1 == v2 && m1 < m2));}//计算凸包void CalcConvexHull(PTARRAY &vecSrc) { //点集中至少应有3个点,才能构成多边形 if (vecSrc.size() < 3) { return; } //查找基点 POINT ptBase = vecSrc.front(); //将第1个点预设为最小点 for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) { //如果当前点的y值小于最小点,或y值相等,x值较小 if (i->y < ptBase.y || (i->y == ptBase.y && i->x > ptBase.x)) { //将当前点作为最小点 ptBase = *i; } } //计算出各点与基点构成的向量 for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end();) { //排除与基点相同的点,避免后面的排序计算中出现除0错误 if (*i == ptBase) { i = vecSrc.erase(i); } else { //方向由基点到目标点 i->x -= ptBase.x, i->y -= ptBase.y; ++i; } } //按各向量与横坐标之间的夹角排序 sort(vecSrc.begin(), vecSrc.end(), &CompareVector); //删除相同的向量 vecSrc.erase(unique(vecSrc.begin(), vecSrc.end()), vecSrc.end()); //计算得到首尾依次相联的向量 for (PTARRAY::reverse_iterator ri = vecSrc.rbegin(); ri != vecSrc.rend() - 1; ++ri) { PTARRAY::reverse_iterator riNext = ri + 1; //向量三角形计算公式 ri->x -= riNext->x, ri->y -= riNext->y; } //依次删除不在凸包上的向量 for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) { //回溯删除旋转方向相反的向量,使用外积判断旋转方向 for (PTARRAY::iterator iLast = i - 1; iLast != vecSrc.begin();) { int v1 = i->x * iLast->y, v2 = i->y * iLast->x; //如果叉积小于0,则无没有逆向旋转 //如果叉积等于0,还需判断方向是否相逆 if (v1 < v2 || (v1 == v2 && i->x * iLast->x > 0 && i->y * iLast->y > 0)) { break; } //删除前一个向量后,需更新当前向量,与前面的向量首尾相连 //向量三角形计算公式 i->x += iLast->x, i->y += iLast->y; iLast = (i = vecSrc.erase(iLast)) - 1; } } //将所有首尾相连的向量依次累加,换算成坐标 vecSrc.front().x += ptBase.x, vecSrc.front().y += ptBase.y; for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) { i->x += (i - 1)->x, i->y += (i - 1)->y; } //添加基点,全部的凸包计算完成 vecSrc.push_back(ptBase);}int main(void) { int nPtCnt = 100; //生成的随机点数 PTARRAY vecSrc, vecCH; for (int i = 0; i < nPtCnt; ++i) { POINT ptIn = { rand() % 20, rand() % 20 }; vecSrc.push_back(ptIn); cout << ptIn.x << ", " << ptIn.y << endl; } CalcConvexHull(vecSrc); cout << "
Convex Hull:
"; for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end(); ++i) { cout << i->x << ", " << i->y << endl; } return 0;} |
概念
凸包(Convex Hull)是一个计算几何(图形学)中的概念。用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边型,它能包含点集中所有点的。严谨的定义和相关概念参见维基百科:凸包。
这个算法是由数学大师葛立恒(Graham)发明的,他曾经是美国数学学会(AMS)主席、AT&T首席科学家以及国际杂技师协会(IJA)主席。(太汗了,这位大牛还会玩杂技~)
问题
给定平面上的二维点集,求解其凸包。
过程
1. 在所有点中选取y坐标最小的一点H,当作基点。如果存在多个点的y坐标都为最小值,则选取x坐标最小的一点。坐标相同的点应排除。然后按照其它各点p和基点构成的向量<H,p>与x轴的夹角进行排序,夹角由大至小进行顺时针扫描,反之则进行逆时针扫描。实现中无需求得夹角,只需根据向量的内积公式求出向量的模即可。以下图为例,基点为H,根据夹角由小至大排序后依次为H,K,C,D,L,F,G,E,I,B,A,J。下面进行逆时针扫描。

2. 线段<H, K>一定在凸包上,接着加入C。假设线段<K, C>也在凸包上,因为就H,K,C三点而言,它们的凸包就是由此三点所组成。但是接下来加入D时会发现,线段<K, D>才会在凸包上,所以将线段<K, C>排除,C点不可能是凸包。
3. 即当加入一点时,必须考虑到前面的线段是否会出现在凸包上。从基点开始,凸包上每条相临的线段的旋转方向应该一致,并与扫描的方向相反。如果发现新加的点使得新线段与上线段的旋转方向发生变化,则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断,设新加入的点为pn + 1,上一点为pn,再上一点为pn - 1。顺时针扫描时,如果向量<pn - 1, pn>与<pn, pn + 1>的叉积为正(逆时针扫描判断是否为负),则将上一点删除。删除过程需要回溯,将之前所有叉积符号相反的点都删除,然后将新点加入凸包。

在上图中,加入K点时,由于线段<H,K>相对于<H,C>为顺时针旋转,所以C点不在凸包上,应该删除,保留K点。接着加入D点,由于线段<K, D>相对<H, K>为逆时针旋转,故D点保留。按照上述步骤进行扫描,直到点集中所有的点都遍例完成,即得到凸包。
复杂度
这个算法可以直接在原数据上进行运算,因此空间复杂度为O(1)。但如果将凸包的结果存储到另一数组中,则可能在代码级别进行优化。由于在扫描凸包前要进行排序,因此时间复杂度至少为快速排序的O(nlgn)。后面的扫描过程复杂度为O(n),因此整个算法的复杂度为O(nlgn)。
C++/STL实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
|
#include <algorithm>#include <iostream>#include <vector>#include <math.h>using namespace std;//二维点(或向量)结构体定义#ifndef _WINDEF_struct POINT { int x; int y; };#endiftypedef vector<POINT> PTARRAY;//判断两个点(或向量)是否相等bool operator==(const POINT &pt1, const POINT &pt2) { return (pt1.x == pt2.x && pt1.y == pt2.y);}// 比较两个向量pt1和pt2分别与x轴向量(1, 0)的夹角bool CompareVector(const POINT &pt1, const POINT &pt2) { //求向量的模 float m1 = sqrt((float)(pt1.x * pt1.x + pt1.y * pt1.y)); float m2 = sqrt((float)(pt2.x * pt2.x + pt2.y * pt2.y)); //两个向量分别与(1, 0)求内积 float v1 = pt1.x / m1, v2 = pt2.x / m2; return (v1 > v2 || (v1 == v2 && m1 < m2));}//计算凸包void CalcConvexHull(PTARRAY &vecSrc) { //点集中至少应有3个点,才能构成多边形 if (vecSrc.size() < 3) { return; } //查找基点 POINT ptBase = vecSrc.front(); //将第1个点预设为最小点 for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) { //如果当前点的y值小于最小点,或y值相等,x值较小 if (i->y < ptBase.y || (i->y == ptBase.y && i->x > ptBase.x)) { //将当前点作为最小点 ptBase = *i; } } //计算出各点与基点构成的向量 for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end();) { //排除与基点相同的点,避免后面的排序计算中出现除0错误 if (*i == ptBase) { i = vecSrc.erase(i); } else { //方向由基点到目标点 i->x -= ptBase.x, i->y -= ptBase.y; ++i; } } //按各向量与横坐标之间的夹角排序 sort(vecSrc.begin(), vecSrc.end(), &CompareVector); //删除相同的向量 vecSrc.erase(unique(vecSrc.begin(), vecSrc.end()), vecSrc.end()); //计算得到首尾依次相联的向量 for (PTARRAY::reverse_iterator ri = vecSrc.rbegin(); ri != vecSrc.rend() - 1; ++ri) { PTARRAY::reverse_iterator riNext = ri + 1; //向量三角形计算公式 ri->x -= riNext->x, ri->y -= riNext->y; } //依次删除不在凸包上的向量 for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) { //回溯删除旋转方向相反的向量,使用外积判断旋转方向 for (PTARRAY::iterator iLast = i - 1; iLast != vecSrc.begin();) { int v1 = i->x * iLast->y, v2 = i->y * iLast->x; //如果叉积小于0,则无没有逆向旋转 //如果叉积等于0,还需判断方向是否相逆 if (v1 < v2 || (v1 == v2 && i->x * iLast->x > 0 && i->y * iLast->y > 0)) { break; } //删除前一个向量后,需更新当前向量,与前面的向量首尾相连 //向量三角形计算公式 i->x += iLast->x, i->y += iLast->y; iLast = (i = vecSrc.erase(iLast)) - 1; } } //将所有首尾相连的向量依次累加,换算成坐标 vecSrc.front().x += ptBase.x, vecSrc.front().y += ptBase.y; for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) { i->x += (i - 1)->x, i->y += (i - 1)->y; } //添加基点,全部的凸包计算完成 vecSrc.push_back(ptBase);}int main(void) { int nPtCnt = 100; //生成的随机点数 PTARRAY vecSrc, vecCH; for (int i = 0; i < nPtCnt; ++i) { POINT ptIn = { rand() % 20, rand() % 20 }; vecSrc.push_back(ptIn); cout << ptIn.x << ", " << ptIn.y << endl; } CalcConvexHull(vecSrc); cout << "
Convex Hull:
"; for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end(); ++i) { cout << i->x << ", " << i->y << endl; } return 0;} |