并查集
并查集是什么
并查集是一种用来管理元素分组情况的数据结构。并查集可以高效地进行以下两种操作:
1,查询元素x和y是否属于同一组
2,合并元素x和y所在的组
但是并查集并不支持分割操作。
并查集的结构
并查集也是使用树形结构实现的,不过并不是二叉树。
初始的时候,每一个元素各为一个组,然后通过输入的信息,将其一个个合并。合并的图示如下:
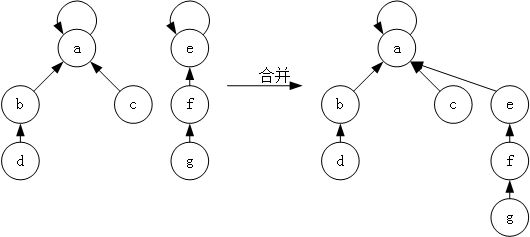
但是既然是树形结构,就有可能退化成链,这样的话操作复杂度就会变的非常大。因此需要优化,一般并查集有两种优化:
1,秩优化;2,路径压缩。
秩优化:
对于每刻树,记录这棵树的高度rank,在合并时,如果两颗树的rank不同,将rank小的接到rank大的后面。
路径压缩:
最常用的优化,只要一个点向上走到了一次根节点,就将其直接连到根节点上。简单来说:你父亲的父亲就是你的父亲——反查理马特——并查集。
加入两个优化后,并查集的复杂度就降的非常低了,每次操作的平均复杂度为O(a(n)),这里a(n)是阿克曼函数的反函数,一般a(n)小于4,因此可以直接看作常数。
Code:
//It is made by HolseLee on 13th Mar 2018 //Luogu.org P3367 #include<cstdio> #include<cstring> #include<cstdlib> #include<cmath> #include<iostream> #include<iomanip> #include<algorithm> using namespace std; const int N=1e4+7; int n,m,fa[N],rank[N]; inline int find(int x) { return fa[x]==x?x:fa[x]=find(fa[x]); } inline void unite(int x,int y) { x=find(x),y=find(y); if(x!=y) { if(rank[x]<rank[y]) { fa[x]=y; } else { fa[y]=x; if(rank[x]==rank[y]) rank[x]++; } } } inline bool check(int x,int y) { return find(x)==find(y); } int main() { ios::sync_with_stdio(false); cin>>n>>m;int opt,x,y; for(int i=1;i<=n;i++) fa[i]=i,rank[i]=1; for(int i=1;i<=m;i++) { cin>>opt>>x>>y; if(opt==1) unite(x,y); else { if(check(x,y)) printf("Y "); else printf("N "); } } return 0; }
练习题
Luogu.org P1111 修复公路
Luogu.org P1195 口袋的天空
Luogu.org P1196 银河英雄传说
Luogu.org P1197 星球大战
POJ 1988 Cube Stacking
POJ 1182 食物链
HDU 3038 How Many Answers Are Wrong
HDU 3635 DragonBalls