神精度……………………这都能过。随便算就好了,根本不用操心
就是把六边形补全成三角形。然后去掉补的三个三角形,然后面积除以边长1的三角形的面积就可以。。。。
#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<iostream>
#include<algorithm>
#include<bitset>
#include<climits>
#include<list>
#include<iomanip>
#include<stack>
#include<set>
using namespace std;
const double pi=acos(-1.0);
double a[6];
int main()
{
for(int i=0;i<6;i++)
cin>>a[i];
double side=a[0]+a[1]+a[2],area=pow(side,2)*sin(pi/3)*cos(pi/3);
area-=pow(a[0],2)*sin(pi/3)*cos(pi/3)+pow(a[2],2)*sin(pi/3)*cos(pi/3)+pow(a[4],2)*sin(pi/3)*cos(pi/3);
double ans=area/(sin(pi/3)*cos(pi/3));
printf("%.0f",ans);
}
Gerald got a very curious hexagon for his birthday. The boy found out that all the angles of the hexagon are equal to 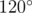 .
Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.
.
Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.
He painted a few lines, parallel to the sides of the hexagon. The lines split the hexagon into regular triangles with sides of 1 centimeter. Now Gerald wonders how many triangles he has got. But there were so many of them that Gerald lost the track of his counting. Help the boy count the triangles.
The first and the single line of the input contains 6 space-separated integers a1, a2, a3, a4, a5 and a6 (1 ≤ ai ≤ 1000) — the lengths of the sides of the hexagons in centimeters in the clockwise order. It is guaranteed that the hexagon with the indicated properties and the exactly such sides exists.
Print a single integer — the number of triangles with the sides of one 1 centimeter, into which the hexagon is split.
1 1 1 1 1 1
6
1 2 1 2 1 2
13
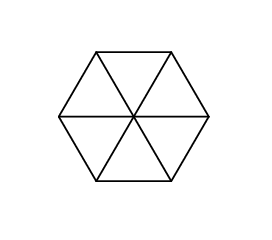
This is what Gerald's hexagon looks like in the first sample:
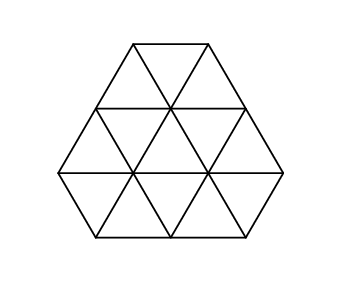
And that's what it looks like in the second sample: