2.简单散点图
接着上一章讲的,另一种常用的图表类型是简单散点图,它是折线图的近亲。不像折线图,图中的点连接起来组成连线,散点图中的点都是独立分布的点状、圆圈或其他形状。本节开始我们也是首先将需要用到的图表工具和函数导入到 Pycharm 中:
import matplotlib.pyplot as plt plt.style.use('seaborn-whitegrid') import numpy as np
使用 plt.plot 绘制散点图
在上一节中,我们介绍了plt.plot/ax.plot方法绘制折线图。这两个方法也可以同样用来绘制散点图:
x = np.linspace(0, 10, 30) y = np.sin(x) plt.plot(x, y, 'o', color='black'); plt.show()
传递给函数的第三个参数是使用一个字符代表的图表绘制点的类型。就像你可以使用'-'或'--'来控制线条的风格那样,点的类型风格也可以使用短字符串代码来表示。所有可用的符号可以通过plt.plot文档或 Matplotlib 在线文档进行查阅。大多数的代码都是非常直观的,我们使用下面的例子可以展示那些最通用的符号(将上面第1-3行代码改为以下,并开头加上库函数,结尾plt.show()即可):
rng = np.random.RandomState(0) for marker in ['o', '.', ',', 'x', '+', 'v', '^', '<', '>', 's', 'd']: plt.plot(rng.rand(5), rng.rand(5), marker, label="marker='{0}'".format(marker)) plt.legend(numpoints=1) plt.xlim(0, 1.8);
plt.plot(x, y, '-p', color='gray', markersize=15, linewidth=4, markerfacecolor='white', markeredgecolor='gray', markeredgewidth=2) plt.ylim(-1.2, 1.2);
而且这些符号代码可以和线条、颜色代码一起使用,这会在折线图的基础上绘制出散点:
plt.plot(x, y, '-ok');
plt.plot还有很多额外的关键字参数用来指定广泛的线条和点的属性:
plt.plot(x, y, '-p', color='gray', markersize=15, linewidth=4, markerfacecolor='white', markeredgecolor='gray', markeredgewidth=2) plt.ylim(-1.2, 1.2);
plt.plot函数的这种灵活性提供了很多的可视化选择。查阅plt.plot帮助文档获得完整的选项说明。
使用plt.scatter绘制散点图
第二种更强大的绘制散点图的方法是使用plt.scatter函数,它的使用方法和plt.plot类似:
plt.scatter(x, y, marker='o');
plt.scatter和plt.plot的主要区别在于,plt.scatter可以针对每个点设置不同属性(大小、填充颜色、边缘颜色等),还可以通过数据集合对这些属性进行设置。
让我们通过一个随机值数据集绘制不同颜色和大小的散点图来说明。为了更好的查看重叠的结果,我们还使用了alpha关键字参数对点的透明度进行了调整:
rng = np.random.RandomState(0) x = rng.randn(100) y = rng.randn(100) colors = rng.rand(100) sizes = 1000 * rng.rand(100) plt.scatter(x, y, c=colors, s=sizes, alpha=0.3, cmap='viridis') plt.colorbar(); # 显示颜色对比条
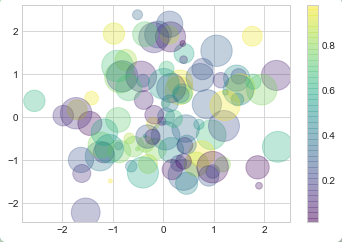
注意图表右边有一个颜色对比条(这里通过colormap()函数输出),图表中的点大小的单位是像素。使用这种方法,散点的颜色和大小都能用来展示数据信息,在希望展示多个维度数据集合的情况下很直观。
例如,当我们使用 Scikit-learn 中的鸢尾花数据集,里面的每个样本都是三种鸢尾花中的其中一种,并带有仔细测量的花瓣和花萼的尺寸数据:
from sklearn.datasets import load_iris iris = load_iris() features = iris.data.T plt.scatter(features[0], features[1], alpha=0.2, s=100*features[3], c=iris.target, cmap='viridis') plt.xlabel(iris.feature_names[0]) plt.ylabel(iris.feature_names[1]);
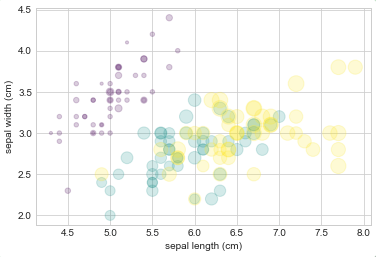
我们可以从上图中看出,可以通过散点图同时展示该数据集的四个不同维度:图中的(x, y)位置代表每个样本的花萼的长度和宽度,散点的大小代表每个样本的花瓣的宽度,而散点的颜色代表一种特定的鸢尾花类型。如上图的多种颜色和多种属性的散点图对于我们分析和展示数据集时都非常有帮助。
plot 和 scatter 对比:性能提醒
除了上面说的plt.plot和plt.scatter对于每个散点不同属性的支持不同之外,还有别的因素影响对这两个函数的选择吗?对于小的数据集来说,两者并无差别,当数据集增长到几千个点时,plt.plot会明显比plt.scatter的性能要高。造成这个差异的原因是plt.scatter支持每个点使用不同的大小和颜色,因此渲染每个点时需要完成更多额外的工作。而plt.plot来说,每个点都是简单的复制另一个点产生,因此对于整个数据集来说,确定每个点的展示属性的工作仅需要进行一次即可。对于很大的数据集来说,这个差异会导致两者性能的巨大区别,因此,对于大数据集应该优先使用plt.plot函数。
3.误差可视化
对于任何的科学测量来说,精确计算误差与精确报告测量值基本上同等重要,如果不是更加重要的话。例如,设想我正在使用一些天文物理学观测值来估算哈勃常数,即本地观测的宇宙膨胀系数。我从一些文献中知道这个值大概是 71 (km/s)/Mpc,而我测量得到的值是 74 (km/s)/Mpc,。这两个值是否一致?在仅给定这些数据的情况下,这个问题的答案是,无法回答。
Mpc(百万秒差距)参见秒差距
如果我们将信息增加一些,给出不确定性:最新的文献表示哈勃常数的值大约是 71 2.5 (km/s)/Mpc,我的测量值是 74 5 (km/s)/Mpc。这两个值是一致的吗?这就是一个可以准确回答的问题了。
在数据和结果的可视化中,有效地展示这些误差能使你的图表涵盖和提供更加完整的信息。
基础误差条
调用一个 Matplotlib 函数就能创建一个基础的误差条:
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
x = np.linspace(0, 10, 50)
dy = 0.8
y = np.sin(x) + dy * np.random.randn(50)
plt.errorbar(x, y, yerr=dy, fmt='.k');
plt.show()
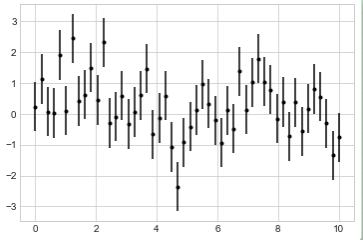
这里的fmt参数是用来控制线条和点风格的代码,与plt.plot有着相同的语法,参见[简单的折线图]和[简单的散点图]。
除了上面的基本参数,errorbar函数还有很多参数可以用来精细调节图表输出。使用这些参数你可以很容易的个性化调整误差条的样式。作者发现通常将误差线条颜色调整为浅色会更加清晰,特别是在数据点比较密集的情况下:
plt.errorbar(x, y, yerr=dy, fmt='o', color='black', ecolor='lightgray', elinewidth=3, capsize=0);
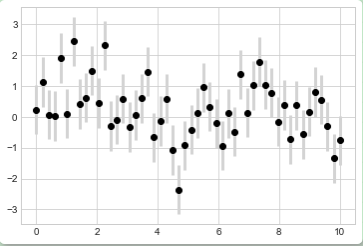
除了上面介绍的参数,你还可以指定水平方向的误差条(xerr),单边误差条和其他很多的参数。参阅plt.errorbar的帮助文档获得更多信息。
连续误差
在某些情况下可能需要对连续值展示误差条。虽然 Matplotlib 没有內建的函数能直接完成这个任务,但是你可以通过简单将plt.plot和plt.fill_between函数结合起来达到目标。
这里我们会采用简单的高斯过程回归方法,Scikit-Learn 提供了 API。这个方法非常适合在非参数化的函数中获得连续误差。我们在这里不会详细介绍高斯过程回归,仅仅聚焦在如何绘制连续误差本身:
译者注:新版的 sklearn 修改了高斯过程回归实现方法,下面代码做了相应修改。
from sklearn.gaussian_process import GaussianProcessRegressor # 定义模型和一些符合模型的点 model = lambda x: x * np.sin(x) xdata = np.array([1, 3, 5, 6, 8]) ydata = model(xdata) # 计算高斯过程回归,使其符合 fit 数据点 gp = GaussianProcessRegressor() gp.fit(xdata[:, np.newaxis], ydata) xfit = np.linspace(0, 10, 1000) yfit, std = gp.predict(xfit[:, np.newaxis], return_std=True) dyfit = 2 * std # 两倍sigma ~ 95% 确定区域
我们现在有了xfit、yfit和dyfit,作为对我们数据的连续拟合值以及误差限。当然我们也可以像上面一样使用plt.errorbar绘制误差条,但是事实上我们不希望在图标上绘制 1000 个点的误差条。于是我们可以使用plt.fill_between函数在误差限区域内填充一道浅色的误差带来展示连续误差:
# 可视化结果 plt.plot(xdata, ydata, 'or') plt.plot(xfit, yfit, '-', color='gray') plt.fill_between(xfit, yfit - dyfit, yfit + dyfit, color='gray', alpha=0.2) plt.xlim(0, 10);
总代码如下:
import matplotlib.pyplot as plt plt.style.use('seaborn-whitegrid') import numpy as np from sklearn.gaussian_process import GaussianProcessRegressor # 定义模型和一些符合模型的点 model = lambda x: x * np.sin(x) xdata = np.array([1, 3, 5, 6, 8]) ydata = model(xdata) # 计算高斯过程回归,使其符合 fit 数据点 gp = GaussianProcessRegressor() gp.fit(xdata[:, np.newaxis], ydata) xfit = np.linspace(0, 10, 1000) yfit, std = gp.predict(xfit[:, np.newaxis], return_std=True) dyfit = 2 * std # 两倍sigma ~ 95% 确定区域 # 可视化结果 plt.plot(xdata, ydata, 'or') plt.plot(xfit, yfit, '-', color='gray') plt.fill_between(xfit, yfit - dyfit, yfit + dyfit, color='gray', alpha=0.2) plt.xlim(0, 10); plt.show()
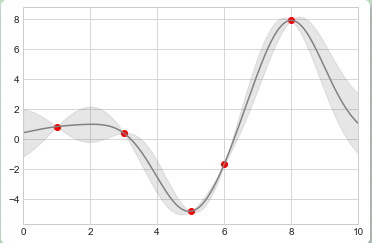
注意上面我们调用fill_between函数:我们传递了的参数包括 x 值,y 值的低限,然后是 y 值的高限,结果是图表中介于低限和高限之间的区域会被填充。
上图为我们提供了一个非常直观的高斯过程回归展示:在观测点的附近,模型会被限制在一个很小的区域内,反映了这些数据的误差比较小。在远离观测点的区域,模型开始发散,反映了这时的数据误差比较大。
如果需要获得plt.fill_between(以及类似的plt.fill函数)更多参数的信息,请查阅函数的帮助文档或 Matplotlib 在线文档。