回溯法之0-1背包问题

 问题描述：  

     给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问:应如何选择装入背包的物品，使得装入背包中物品的总价值最大?例如

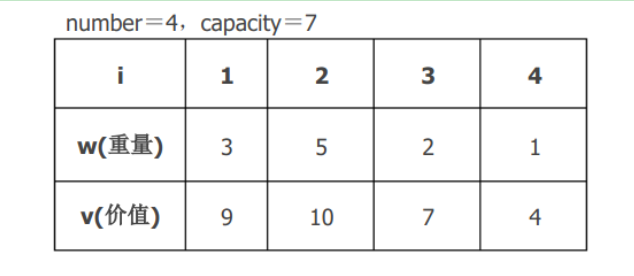
     形式化描述：给定c >0, wi >0, vi >0 , 1≤i≤n.要求找一n元向量(x1,x2,…,xn,), xi∈{0,1}, ∋ ∑ wi xi≤c,且∑ vi xi达最大.即一个特殊的整数规划问题。

      问题解析：0-1背包问题是子集选取问题。0-1 背包问题的解空间可以用子集树表示。在搜索解空间树时，只要其左儿子节点是一个可行节点，搜索就进入左子树。当右子树中有可能含有最优解时，才进入右子树搜索。否则，将右子树剪去。设r是当前剩余物品价值总和，cp是当前价值；bestp是当前最优价值。当cp+r<=bestp时，可剪去右子树。计算右子树上界的更好的方法是将剩余物品依次按其单位价值排序，然后依次装入物品，直至装不下时，再装入物品一部分而装满背包。

     例如：对于0-1背包问题的一个实例，n=4,c=7,p=[9,10,7,4],w=[3,5,2,1]。这4个物品的单位重量价值分别为[3,2,3,5,4]。以物品单位重量价值的递减序装入物品。先装入物品4，然后装入物品3和1.装入这3个物品后，剩余的背包容量为1，只能装0.2的物品2。由此得一个解为[1,0.2,1,1]，其相应价值为22。尽管这不是一个可行解，但可以证明其价值是最优值的上界。因此，对于这个实例，最优值不超过22。

     在实现时，由Bound计算当前节点处的上界。类Knap的数据成员记录解空间树中的节点信息，以减少参数传递调用所需要的栈空间。在解空间树的当前扩展节点处，仅要进入右子树时才计算上界Bound,以判断是否可将右子树剪去。进入左子树时不需要计算上界，因为上界预期父节点的上界相同。算法的具体实现如下：

代码实现：

#include <iostream>
#include <stdio.h>
//#include <conio.h>
using namespace std;
int n;//物品数量
double c;//背包容量
double v[100];//各个物品的价值　value
double w[100];//各个物品的重量　weight
double cw = 0.0;//当前背包重量　current weight
double cp = 0.0;//当前背包中物品总价值　current value
double bestp = 0.0;//当前最优价值best price
double perp[100];//单位物品价值(排序后) per price
int order[100];//物品编号
int put[100];//设置是否装入，为1的时候表示选择该组数据装入，为0的表示不选择该组数据
 
 
//按单位价值排序
void knapsack()
{
    int i,j;
    int temporder = 0;
    double temp = 0.0;
 
    for(i=1;i<=n;i++)
        perp[i]=v[i]/w[i]; //计算单位价值（单位重量的物品价值）
    for(i=1;i<=n-1;i++)
    {
        for(j=i+1;j<=n;j++)
            if(perp[i]<perp[j])//冒泡排序perp[],order[],sortv[],sortw[]
        {
            temp = perp[i];  //冒泡对perp[]排序
            perp[i]=perp[i];
            perp[j]=temp;
 
            temporder=order[i];//冒泡对order[]排序
            order[i]=order[j];
            order[j]=temporder;
 
            temp = v[i];//冒泡对v[]排序
            v[i]=v[j];
            v[j]=temp;
 
            temp=w[i];//冒泡对w[]排序
            w[i]=w[j];
            w[j]=temp;
        }
    }
}
 
//回溯函数
void backtrack(int i)
{   //i用来指示到达的层数（第几步，从0开始），同时也指示当前选择玩了几个物品
    double bound(int i);
    if(i>n) //递归结束的判定条件
    {
        bestp = cp;
        return;
    }
    //如若左子节点可行，则直接搜索左子树;
    //对于右子树，先计算上界函数，以判断是否将其减去
    if(cw+w[i]<=c)//将物品i放入背包,搜索左子树
    {
        cw+=w[i];//同步更新当前背包的重量
        cp+=v[i];//同步更新当前背包的总价值
        put[i]=1;
        backtrack(i+1);//深度搜索进入下一层
        cw-=w[i];//回溯复原
        cp-=v[i];//回溯复原
    }
    if(bound(i+1)>bestp)//如若符合条件则搜索右子树
        backtrack(i+1);
}
 
//计算上界函数，功能为剪枝
double bound(int i)
{   //判断当前背包的总价值cp＋剩余容量可容纳的最大价值<=当前最优价值
    double leftw= c-cw;//剩余背包容量
    double b = cp;//记录当前背包的总价值cp,最后求上界
    //以物品单位重量价值递减次序装入物品
    while(i<=n && w[i]<=leftw)
    {
        leftw-=w[i];
        b+=v[i];
        i++;
    }
    //装满背包
    if(i<=n)
        b+=v[i]/w[i]*leftw;
    return b;//返回计算出的上界
 
}
 
 
 
int main()
{
    int i;
    printf("请输入物品的数量和背包的容量：");
    scanf("%d %lf",&n,&c);
    /*printf("请输入物品的重量和价值：
");
    for(i=1;i<=n;i++)
    {
        printf("第%d个物品的重量：",i);
        scanf("%lf",&w[i]);
        printf("第%d个物品的价值是：",i);
        scanf("%lf",&v[i]);
        order[i]=i;
    }*/
    printf("请依次输入%d个物品的重量:
",n);
    for(i=1;i<=n;i++){
        scanf("%lf",&w[i]);
        order[i]=i;
    }
 
    printf("请依次输入%d个物品的价值:
",n);
    for(i=1;i<=n;i++){
        scanf("%lf",&v[i]);
    }
 
 
    knapsack();
    backtrack(1);
 
 
    printf("最优价值为：%lf
",bestp);
    printf("需要装入的物品编号是：");
    for(i=1;i<=n;i++)
    {
        if(put[i]==1)
            printf("%d ",order[i]);
    }
    return 0;
}

算法效率：

计算上界需要O(n)时间，在最坏情况下有O(2^n)个右儿子节点需要计算上界，故解0-1背包问题的回溯算法所需要的计算时间为O(n2^n)。

运行结果：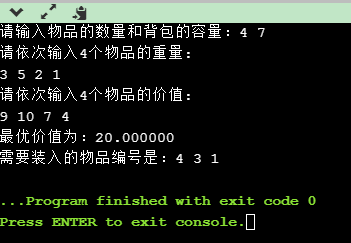

 参考文献：王晓东《算法设计与分析》

                  https://blog.csdn.net/qian2213762498/article/details/79420269?depth_1-