链接:http://codeforces.com/contest/485
One industrial factory is reforming working plan. The director suggested to set a mythical detail production norm. If at the beginning of the day there werex details in the factory storage,
then by the end of the day the factory has to produce (remainder after dividingx bym)
more details. Unfortunately, no customer has ever bought any mythical detail, so all the details produced stay on the factory.
(remainder after dividingx bym)
more details. Unfortunately, no customer has ever bought any mythical detail, so all the details produced stay on the factory.
The board of directors are worried that the production by the given plan may eventually stop (that means that there will be а moment when the current number of details on the factory is divisible bym).
Given the number of details a on the first day and number m check if the production stops at some moment.
The first line contains two integers a and m (1 ≤ a, m ≤ 105).
Print "Yes" (without quotes) if the production will eventually stop, otherwise print "No".
1 5
No
3 6
Yes
x每次加上对m取模的值,假设取模为0输出YES。假设值之前出现过,则进入循环输出No退出
#include <cstdio>
#include <cstring>
int vis[100002];
int main()
{
int a, m;
scanf("%d %d", &a, &m);
memset(vis, 0, sizeof(vis));
while(true)
{
if(a == 0)
{
printf("Yes
");
return 0;
}
if(vis[a])
{
printf("No
");
return 0;
}
vis[a] = 1;
a = (a + a % m) % m;
}
}
Many computer strategy games require building cities, recruiting army, conquering tribes, collecting resources. Sometimes it leads to interesting problems.
Let's suppose that your task is to build a square city. The world map uses the Cartesian coordinates. The sides of the city should be parallel to coordinate axes. The map contains mines with valuable resources, located at some points with integer coordinates. The sizes of mines are relatively small, i.e. they can be treated as points. The city should be built in such a way that all the mines are inside or on the border of the city square.
Building a city takes large amount of money depending on the size of the city, so you have to build the city with the minimum area. Given the positions of the mines find the minimum possible area of the city.
The first line of the input contains number n — the number of mines on the map (2 ≤ n ≤ 1000). Each of the nextn lines contains a pair of integersxi andyi — the coordinates of the corresponding mine ( - 109 ≤ xi, yi ≤ 109). All points are pairwise distinct.
Print the minimum area of the city that can cover all the mines with valuable resources.
2
0 0
2 2
4
2
0 0
0 3
9
给几个点,让这几个点都在一个正方形上或者内部,求正方形的面积的最小值,最上减最下和最右减最左的最大值作为边长
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
int main()
{
int n;
ll x, y;
ll mu, md, ml, mr;
ll ans = 0;
mu = mr = -2147483646;
ml = md = 2147483647;
scanf("%d", &n);
for(int i = 0; i < n; i++)
{
scanf("%I64d %I64d", &x, &y);
mu = max(mu , y);
md = min(md , y);
ml = min(ml , x);
mr = max(mr , x);
}
ans = max((mu - md), (mr - ml)) * max((mu - md), (mr - ml));
printf("%I64d
", ans);
}
Let's denote as 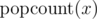 the number of bits set ('1' bits) in the binary representation of the non-negative
integer x.
the number of bits set ('1' bits) in the binary representation of the non-negative
integer x.
You are given multiple queries consisting of pairs of integersl andr. For each query, find thex, such thatl ≤ x ≤ r,
and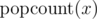 is maximum possible. If there are multiple such numbers find the smallest of them.
is maximum possible. If there are multiple such numbers find the smallest of them.
The first line contains integer n — the number of queries (1 ≤ n ≤ 10000).
Each of the following n lines contain two integersli, ri — the arguments for the corresponding query (0 ≤ li ≤ ri ≤ 1018).
For each query print the answer in a separate line.
3
1 2
2 4
1 10
1
3
7
The binary representations of numbers from 1 to 10 are listed below:
110 = 12
210 = 102
310 = 112
410 = 1002
510 = 1012
610 = 1102
710 = 1112
810 = 10002
910 = 10012
1010 = 10102
给一个区间,求区间里的数转化为二进制后拥有'1'个数最多的那个数。要是拥有'1'的数量同样,取最小的那个数输出。
直接从左端点对1进行或运算,构造出'1'最多且最小的数,直到值大于右端点
#include <cstdio>
#define ll long long
int main()
{
int t;
scanf("%d", &t);
while(t--)
{
ll l, r, tmp, p = 1;
scanf("%I64d %I64d", &l, &r);
for(ll i = 0; i < 63; i++)
{
ll tmp = l | p;
if(tmp > r)
break;
l = tmp;
p <<= 1;
}
printf("%I64d
", l);
}
}
You are given a sequence a consisting ofn integers. Find the maximum possible value of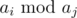 (integer remainder ofai divided byaj), where1 ≤ i, j ≤ n
and ai ≥ aj.
(integer remainder ofai divided byaj), where1 ≤ i, j ≤ n
and ai ≥ aj.
The first line contains integer n — the length of the sequence (1 ≤ n ≤ 2·105).
The second line contains n space-separated integersai (1 ≤ ai ≤ 106).
Print the answer to the problem.
3
3 4 5
2
找a[i] < a[j]中a[j] % a[i]的最大值 , ai的范围不大,用hash做
#include <cstdio>
int const MAX = 2000000 + 10;
int a[MAX];
int main()
{
int n, x, ans = 0;
scanf("%d",&n);
for(int i = 0; i < n; i++)
{
scanf("%d",&x);
a[x] = x;
}
for(int i = 0; i < MAX; i++)
if(a[i] != i)
a[i] = a[i - 1];
for(int i = 2; i < MAX; i++)
if(a[i] == i)
for(int j = i + i - 1; j < MAX; j = j + i)
if(a[j] % i > ans && a[j] > i)
ans = a[j] % i;
printf("%d
",ans);
}
In a kindergarten, the children are being divided into groups. The teacher put the children in a line and associated each child with his or her integer charisma value. Each child should go to exactly one group. Each group should be a nonempty segment of consecutive children of a line. A group's sociability is the maximum difference of charisma of two children in the group (in particular, if the group consists of one child, its sociability equals a zero).
The teacher wants to divide the children into some number of groups in such way that the totalsociability of the groups is maximum. Help him find this value.
The first line contains integer n — the number of children in the line (1 ≤ n ≤ 106).
The second line contains n integersai — the charisma of thei-th child ( - 109 ≤ ai ≤ 109).
Print the maximum possible total sociability of all groups.
5
1 2 3 1 2
3
3
3 3 3
0
In the first test sample one of the possible variants of an division is following: the first three children form a group with sociability 2, and the two remaining children form a group with sociability 1.
In the second test sample any division leads to the same result, the sociability will be equal to 0 in each group.
把一串数列分成若干组,每组的权值为该组中最大值与最小值的差,求全部组的权值和的最大值
#include <cstdio>
#define ll long long
int main()
{
int n, t;
scanf ("%d", &n);
ll ans = 0, t1 = 0, t2 = 0;
for(int i = 0; i < n; i++)
{
scanf("%d", &t);
if (!i || ans + t > t1) t1 = ans + t;
if (!i || ans - t > t2) t2 = ans - t;
ans = t1 - t > t2 + t ? t1 - t : t2 + t;
}
printf("%I64d
", ans);
}