有卡炫富
抛弃learning rate decay吧!
原文:学界 | 抛弃Learning Rate Decay吧!
作者:Elevanth
备注:为雷锋网/AI 科技评论写的一篇论文解读,起因是进一步搜索相关论文时发现了这篇“打脸”的论文,也算奇文共赏析吧~作者水平不高,希望能和大家一起进步!
论文地址: DON’T DECAY THE LEARNING RATE, INCREASE THE BATCH SIZE
真的是生命不息,打脸不止。前几天刚刚总结了常见的learning rate decay方法(参见Tensorflow中learning rate decay的奇技淫巧),最近又看到这篇正在投ICLR2018的盲审,求我现在的心理阴影的面积。。。

然后上arxiv一查,哦,Google爸爸的,干货满满,简直不容反驳。。。

先点题:
不用衰减学习率啦,只要增大Batch Size就可以啦!
摘要:
- 实际上作者在衰减学习率的时候同时也降低了SGD中随机波动
的值;衰减学习率类似于模拟退火;
- 不同于衰减学习率,作者提出了在增加Batch Size的同时保持学习率的策略,既可以保证不掉点,还可以减少参数更新的次数;
- 作者还可以既增加学习率又增大Batch Size,如此可以基本保持test中不掉点又进一步减少参数更新次数;
- 作者对比了自己的模型和另一篇著名论文(Accurate, large minibatch SGD: Training imagenet in 1 hour)中的模型,Batch Size:65536 - 8192;正确率:77% - 76%;参数更新次数:2500 - 14000;
随即梯度下降法与曲线优化
传统的学习率遵循以下两个约束:
直观来看,公式1约束最小值优化的参数一定存在,公式2保证了衰减学习率有助于快速收敛至最小值处,而不是由于噪声在震荡。
然而以上结论是给予Batch Size不变推导出的。作者基于前作(A BAYESIAN PERSPECTIVE ON GENERALIZATION AND STOCHASTIC GRADIENT DESCENT)推导出另一个解释优化过程的模型,并指出可以通过找到某个最优化的随机波动值 (其中
为学习率 ,
为训练数据集大小,
为Batch Size大小),使得模型达到最优值。
模拟退火法和泛化能力下降
广泛的研究结果指出小Batch Size训练的模型在test中的泛化能力比大Batch Size的要好。前作中还得出了固定学习率下的最大Batch Size优化值 ,并验证了
与随机噪声值
有关。
研究者认为小Batch中的随机误差有助于SGD的收敛,尤其是在非凸曲线优化问题上。噪声可以帮助SGD收敛至所谓平滑最小值(flat minima)而不是尖锐最小值(sharp minima)以保证test的泛化特性。
作者发现大部分研究者在训练过程中都使用了‘early stop’的方法(当验证集的点数不再增高时停止训练),因此我们实际上有意的阻止了网络到达最小值。衰减学习率的成功是经验式的。具体过程可以类比于模拟退火法中,较大的初始噪音有助于探索更大范围内的参数空间而不是很快地陷入局部最优值;一旦我们找到了可能的最优区域后开始减少噪声来finetune到最优值。
而这也能解释为什么近来越来越多的研究者开始使用cosine式衰减学习率或阶梯形的衰减——物理退火法中,缓慢衰减温度是系统收敛到某些锐利的全局最小值;而离散地降低温度则有利于收敛到不是最低但足够鲁棒的区域。
有效的学习率和累积变量
许多研究者开始使用带momentum的SGD下降法,其噪声值与原始SGD稍有不同:
当 时该噪声将退化为原始SGD噪声。对比两种SGD可以得出带momentum的SGD方法的有效学习率应为
。
对比原始SGD,我们可以推导:成比例的放大 可以保持模型性能。然而,作者发现若成比例的缩放学习率
和Batch Size表现良好,但是若按照
倍缩放Batch Size和冲量系数
的话则会导致test性能下降。这是因为冲量式的更新在时间上是累积的,因此当
设置较大时需要额外的训练次数才能保证模型处于相同水平,原文的补充材料中有较详细的分析,此处不作解释。
随着冲量系数 的增大,还会增加网络忘记旧的梯度的时间(该时间和
成正比),一旦时间跨度达到几个epoch以上时,损失空间将会变得不利调整从而阻碍训练。这种情况在学习率衰减的时候尤其明显。这也是为什么有些论文推荐在初始的若干epoch时提升学习率。然而,在我们的大Batch Size实验中,这种做法却会带来系统不稳定性。
实验对比
实验中使用的网络是 “16-4”宽型残差网络结构(wide ResNet architecture),使用了 ghost batch norm方法来保证平均梯度与Batch Size不相关。
实验中使用的对比策略是阶梯形的,学习率阶梯形下降,对应的,Batch Size阶梯形上升。
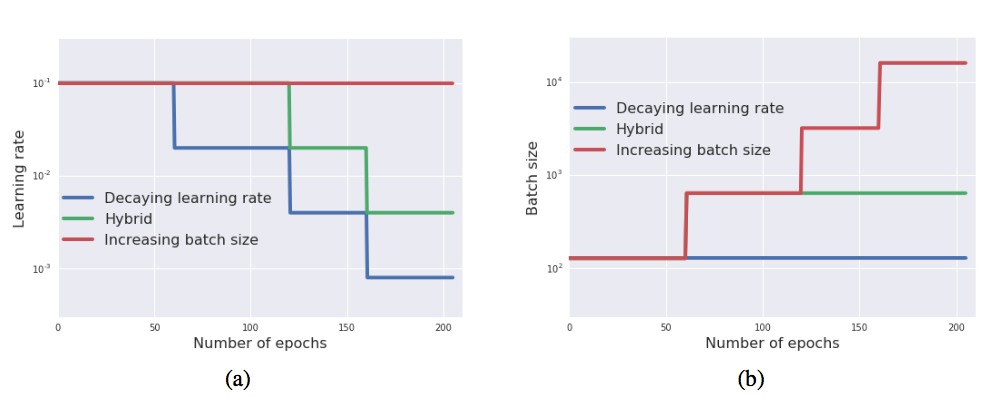
图中,蓝线代表常见的保持Batch Size,逐步衰减学习率的方法;红线代表与之相反的,保持学习率,相应的上升Batch Size的策略;绿线模拟真实条件下,上升Batch Size达到显存上限的时候,再开始下降学习率的策略。
该实验可以验证两个问题:
学习率下降是否是必须的——若是则三条曲线应不同;
是否是因为随机噪声的变化导致结果不同——若是则三条曲线相同;
实验结果如下(a)所示,并验证了随机噪声与训练曲线的相关性。
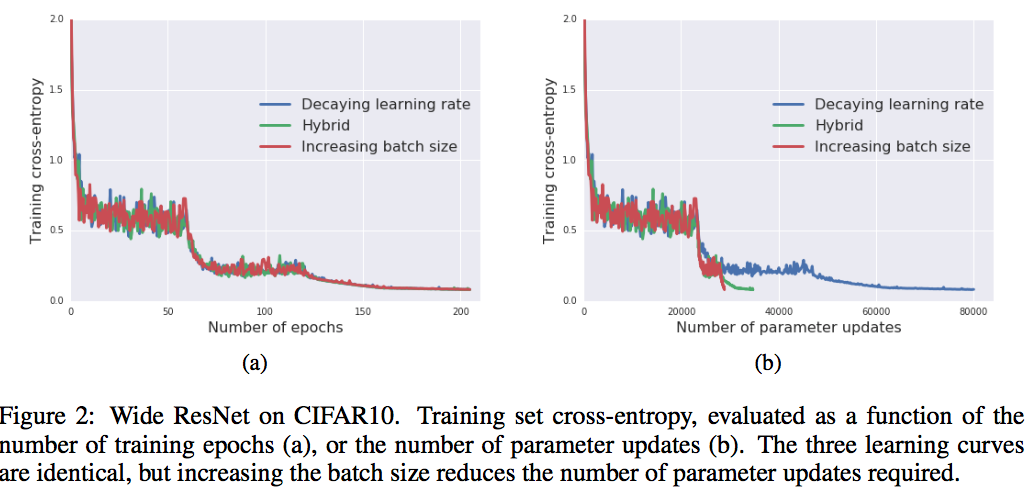
实验结果(b)进一步显示增大Batch Size的好处,观察损失值与参数更新次数的关系,显然,增大Batch Size的方法中参数更新的次数远少于衰减学习率的策略。
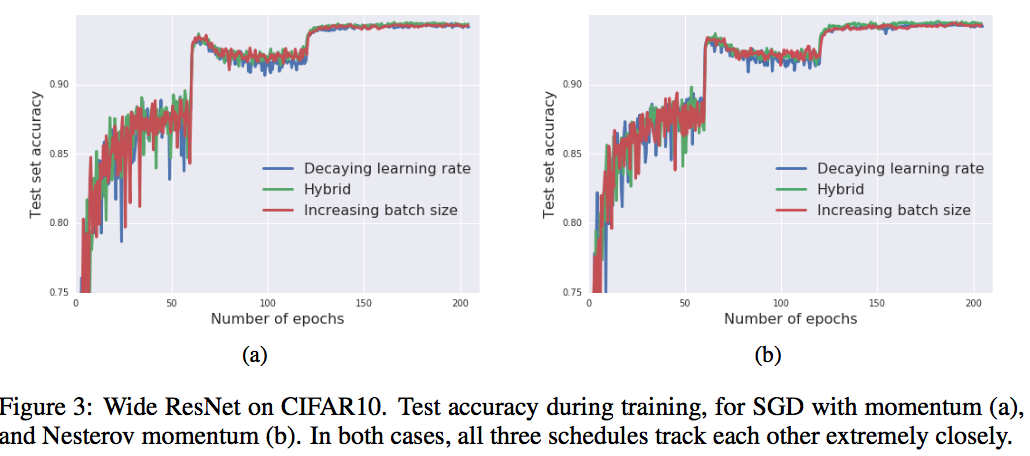
下图是两种不同的梯度下降策略的test结果,显然效果相差不大。
增大学习率策略
作者准备了四组实验:
- Original training schedule:初始学习率设为0.1,momentum为0.9,Batch Size为128,采用衰减学习率策略,每阶段减少5倍;
- Increasing batch size:初始学习率设为0.1,momentum为0.9,Batch Size为128,采用增大Batch Size策略,每阶段增加5倍;
- Increased initial learning rate:初始学习率设为0.5,momentum为0.9,Batch Size为640,采用增大Batch Size策略,每阶段增加5倍;
- Increased momentum coefficient:初始学习率设为0.5,momentum为0.98,Batch Size为3200,采用增大Batch Size策略,每阶段增加5倍;
当Batch Size增加到最大值 后即不再增加,以保证
,并相应的开始减少学习率。
结果如下所示,结论与上文相同,方法4的结果稍差也在章节 有效的学习率和累积变量 中有所解释。
训练IMAGENET只用更新2500次参数
论文Accurate, large minibatch SGD: Training imagenet in 1 hour中的参数与试验参数设置和结果对比如下:
上述论文中的Batch Size已经达到了保持网络稳定的最大值,为了进一步扩大Batch Size可以适当增大momentum的值。最终,作者的网络达到了显存的上限 并保证了
。其参数设置与结果如下所示,可以看到准确率下降不大但是有效减少了参数的更新次数。
增大Batch Size就可以不用衰减学习率了,emmm,听起来很有道理,但是总感觉哪里不对、、、

最后,祝大家炼丹愉快!